§ 5. Законы операций над множествами

1. Коммутативные законы

А  В = В Ç А

А  В = В È А

2. Ассоциативные законы

А Ç (В Ç С) = (А Ç В) Ç С

А È (В È С) = (А È В) È С

3. Дистрибутивные законы

А Ç (В È С) = (А Ç В) È (А Ç С)

А È (В Ç С) = (А È В) Ç (А È С)

4. А Ç А = А

А È А = А

5. А Ç I = А

А È I = I

6. А Ç  = 

А È Æ = А

7. А Ç = Æ

А È =I

8.

9. А \ В = А Ç

10. =А

Контрольные вопросы

1. Что понимают под множеством?

2. Как называют объекты, из которых образовано множество?

3. Какое множество называют пустым?

4. Какие множества называют конечными и бесконечными?

5. В каком случае считают, что множество задано?

6. Укажите способы задания множеств.

7. В каком случае множество А является подмножеством множестваВ?

8. Какие подмножества называют собственными и несобственными?

9. Какие множества называют равными?

10. Сформулируйте свойство равенства множеств.

11. Какое множество называют пересечением, объединением, разностью множеств, дополнением одного множества до другого, дополнением множества до универсального?

§ 6. Число элементов объединения двух и трех конечных множеств

В математике часто приходится решать задачи, в которых требуется определить число элементов в множестве, либо в объединении или пересечении множеств.

Условимся число элементов конечного множества А обозначать п (А).

Пусть А = {a, b, c, d}, п (А) = 4; В = {e, f}, п (В) = 2. Множества А и В не пересекаются, т.е. А  В = .

А  В ={a, b, c, d, e, f}, п (А  В) = 6, т.е. п (А  В) = п (А) + п (В).

Рассмотрим еще один пример. А = {a, b, c, d}, п (А) = 4; В = { c, d, e}, п (В) = 3. В данном примере множества А и В пересекаются, т.е. А  В  .

А  В = {a, b, c, d, e}, п (А  В) = 5, т.е. п (А  В)  п (А) + п (В).

Вообще, если заданы конечные множества, такие что А  В  , то число элементов в их объединении подсчитывают по формуле

п (А  В) = п (А) + п (В) – п (А  В).

Если даны три конечных множества А, В, С, то число элементов в их объединении можно найти по формуле:

п (А  В  С) = п (А) + п (В) + п (С) – п (А  В) – п (А  С) – п (В  С) + + п (А  В  С)

§ 7. Понятие разбиения множества на классы

Понятие множества и операций над множествами позволяют уточнить наше представление о классификации.

Любая классификация связана с разбиением некоторого множества объектов на подмножества.

Определение. Множество А разбито на классы А₁, А₂, ..., А_п, если:

1. подмножества А₁, А₂, ..., А_п не пусты;

2. подмножества А₁, А₂, ..., А_п попарно не пересекаются;

3. объединение подмножеств совпадает с множеством А.

Если не выполнено хотя бы одно свойство, то классификацию считают неправильной.

Например, если множество треугольников разбить на остроугольные, прямоугольные и тупоугольные, то разбиение будет выполнено верно, т.к. выполнены все условия, данные в определении.

Если из множества треугольников выделить подмножества равносторонних, равнобедренных и разносторонних треугольников, то разбиения мы не получим, т.к. множество равносторонних треугольников является подмножеством равнобедренных треугольников, т.е. не выполняется второе условие разбиения множества на классы.

Пример 1. Пусть А – множество двузначных чисел. Рассмотрим на этом множестве свойство «быть четным».

А

М

А₁

А₂

ножествоА разбилось на два подмножества:

А₁ – множество четных чисел,

А₂ – множество нечетных чисел, при этом

А₁  А₂ = А и А₁  А₂ = .

Т.о. задание одного свойства приводит к разбиению этого множества на 2 класса.

Пример 2. Пусть А – множество треугольников. Рассмотрим на данном множестве два свойства: «быть прямоугольным» и «быть равнобедренным». При помощи этих свойств из множества треугольников можно выделить 2 подмножества: В – множество прямоугольных треугольников и С – множество равнобедренных треугольников. Эти множества пересекаются, но ни одно из них не является подмножеством другого.

По рисунку видно, что получилось 4 класса:

I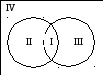 – В  С – множество равнобедренных прямоугольных треугольников;

II – В  – множество прямоугольных, но не равнобедренных треугольников;

III –  С – множество равнобедренных, но не прямоугольных треугольников;

IV –  – множество не равнобедренных и не прямоугольных треугольников.

Т.о. с помощью двух свойств множество разбилось на 4 класса, таких, что их пересечение пусто, а их объединение составляет множество А.

Следует отметить, что задание двух свойств приводит к разбиению множества на 4 класса не всегда.

Пример 3. Пусть А – множество треугольников. Рассмотрим на данном множестве два свойства: «быть прямоугольным» и «быть остроугольным». При помощи этих свойств из множества треугольников можно выделить 2 подмножества: В – множество прямоугольных треугольников и С – множество остроугольных треугольников. Эти множества не пересекаются. По рисунку видно, что при помощи этих свойств множество треугольников разбивается на три класса:

I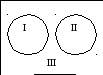– множество прямоугольных треугольников;

II – множество остроугольных треугольников;

III – множество не прямоугольных, не остроугольных треугольников.