§ 3. Отношение эквивалентности. Связь отношения эквивалентности с разбиением множества на классы

Определение. ОтношениеR на множествеХ называется отношениемэквивалентности, если оно рефлексивно, симметрично и транзитивно.

Пример. Рассмотрим отношение «ходнокурснику» на множестве студентов педфака. Оно обладает свойствами:

1. рефлексивности, т.к. каждый студент является однокурсником самому себе;

2. симметричности, т.к. если студент хявляется однокурсником студентау, то и студентуявляется однокурсником студентах;

3. транзитивности, т.к. если студент х- однокурснику, а студенту– однокурсникz, то студентх будет однокурсником студентаz.

Таким образом, данное отношение обладает свойствами рефлексивности, симметричности и транзитивности, а значит, является отношением эквивалентности. При этом множество студентов педфака можно разбить на подмножества, состоящие из студентов, обучающихся на одном курсе. Получаем 5 подмножеств.

Отношением эквивалентности являются также, например, отношение параллельности прямых, отношение равенства фигур. Каждое такое отношение связано с разбиением множества на классы.

Теорема. Если на множествеХзадано отношение эквивалентности, то оно разбивает это множество на попарно непересекающиеся подмножества (классы эквивалентности).

Верно и обратное утверждение: если какое-либо отношение, заданное на множестве Х, порождает разбиение этого множества на классы, то оно является отношением эквивалентности.

Пример. На множествеХ= {1; 2; 3; 4; 5; 6; 7; 8} задано отношение «иметь один и тот же остаток при делении на 3». Является ли оно отношением эквивалентности?

Построим граф данного отношения:

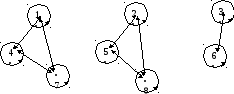
Данное отношение обладает свойствами рефлексивности, симметричности и транзитивности, следовательно, является отношение эквивалентности и разбивает множество Х на классы эквивалентности. В каждом классе эквивалентности будут числа, которые при делении на 3 дают один и тот же остаток:Х₁= {3; 6},Х₂= {1; 4; 7},Х₃= {2; 5; 8}.

Считают, что класс эквивалентности определяется любым своим представителем, т.е. произвольным элементом этого класса. Так, класс равных дробей можно задать, указав любую дробь, принадлежащую этому классу.

В начальном курсе математики также встречаются отношения эквивалентности, например, «выражения хиуимеют одинаковые числовые значения», «фигурахравна фигуреу».

§ 4. Отношение порядка. Упорядоченные множества

Определение.ОтношениеR на множествеХ называется отношениемпорядка, если оно транзитивно и асимметрично или антисимметрично.

Определение.ОтношениеR на множествеХ называется отношениемстрогого порядка, если оно транзитивно и асимметрично.

Примерыотношений строгого порядка: «больше» на множестве натуральных чисел, «выше» на множестве людей и др.

Определение.ОтношениеR на множествеХ называется отношением нестрогого порядка, если оно транзитивно и антисимметрично.

Примерыотношений нестрогого порядка: «не больше» на множестве действительных чисел, «быть делителем» на множестве натуральных чисел и др.

Определение. МножествоХназываютупорядоченным, если на нем задано отношение порядка.

Пример. На множествеХ= {1; 2; 3; 4; 5} заданы два отношения: «ху» и «х– делительу».

Оба эти отношения обладают свойствами рефлексивности, антисимметричности и транзитивности (постройте графы и проверьте свойства самостоятельно), т.е. являются отношением нестрогого порядка. Но первое отношение обладает свойством связности, а второе – нет.

Определение.Отношение порядкаR на множествеХ называетсяотношением линейного порядка, если оно обладает свойством связности.

В начальной школе изучаются многие отношения порядка. Уже в первом классе водятся отношение «меньше», «больше» на множестве натуральных чисел, «короче», «длиннее» на множестве отрезков и др.