3.4.4. Реализация систем в пространстве состояний

Для одной и той же системы в пространстве состояний можно предложить разные описания (A, B, C, D) в зависимости от того, как выбраны переменные состояния.

При составлении моделей динамических систем в пространстве состояний исходными часто являются описания отдельных звеньев системы в форме дифференциальных уравнений с постоянными коэффициентами.

Рассмотрим составление уравнений состояния для таких звеньев путем приведения их к одному из распространенных видов канонической формы.

Пусть одномерная система задана дифференциальным уравнением порядка n следующего вида:

(3.11)

которому отвечает передаточная функция

(3.12)

u(t), y(t) – вход и выход системы соответственно;

a_{i ,} b_j– коэффициенты полиномов, в общем случае функции времени;

i = [1 – n]; j = [1 – m]; m  n.

Правую часть выражения (3.12) умножим и поделим на pⁿ (pⁿ / pⁿ) и получим:

(3.13)

где

(3.14)

или

(3.15)

Полученные зависимости (3.13) - (3.15) являются представлением исходного уравнения (3.12) в канонической форме.

Используя эти зависимости, а именно - (3.13) и (3.15) – легко может быть получена эквивалентная структурная схема, моделирующая данную систему, которая представлена на рисунке 3.7. Здесь обозначены соответствующие и переменные состоянияX.

Легко проверить, что последней схеме отвечают уравнения состояния

(3.16)

Матрицы A, B, C имеют вид

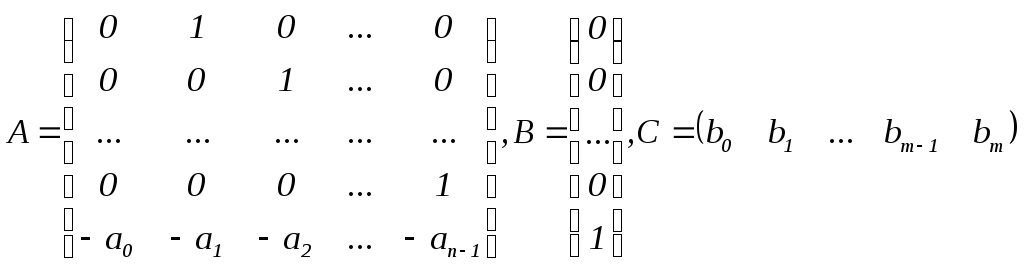(3.17)

Как следует из рассмотрения (3.16), (3.17), элементы матриц уравнений состояния получаются непосредственно из коэффициентов передаточной функции (3.12).

Приведем примеры использования описанного метода представления дифференциальных уравнений.

Пример 2.

Интегро-дифференцирующее динамическое звено описывается следующим операторным уравнением (первого порядка):

(3.18)

Приведем его к стандартной форме (3.12)

(3.19)

где

Соответствующая структурная схема, реализующая данное уравнение и получаемая из схемы для общего случая (см. рис. 3.7), имеет вид, представленный на рис. 3.8.

Пример 3.

Дано операторное уравнение второго порядка:

Этим уравнением моделируются динамические характеристики инерционного и форсирующего звеньев второго порядка.

Преобразуя, приведем его к стандартной форме и получим

где

С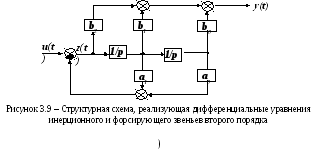оответствующая структурная схема, получаемая из схемы для общего случая (см. рисунок 3.7), имеет вид, представленный на рисунке 3.9.

3.5. Методы построения математических моделей и их применение в сапр

3.5.1. Методы построения математических моделей

При построении математических моделей систем управления будем исходить из уровня описания САУ “система - устройство – элемент” [18].

Наибольшие трудности возникают при построении математических моделей объекта управления.

Это связано с тем, что необходим учет физических процессов и явлений в этих объектах.

Различают:

• графические;

• аналитические;

• численные

методы построения математических моделей САУ.

Графические методы используются при построении математических моделей на верхнем уровне их описания в виде структурных схем и их графовых эквивалентов. В этом случае САУ представляется как сложная система, состоящая из устройств и элементов. Внутренне содержание устройств обычно отражается типовыми звеньями.

При аналитическом построении математических моделей исходными являются:

• общие законы физики (вообще природы);

• результаты обобщения опыта.

Основные законы – это закон сохранения энергии, массы, импульса и др. и вытекающие из них вариационные принципы (наименьшего действия), непрерывности материальных потоков, теплового баланса и др.

приложение этих принципов приводит к тому или иному физическому устройству приводит к различным выражениям.

Численные методы формирования включают в себя последовательность операций по обработке и анализу априорной и апостиорной числовой информации об объекте.

В результате анализа получается структура и параметры математической модели объекта.

При этом обычно имеет место следующая последовательность операций.

1. Задается модель зависимости между входными и выходными переменными в статике.

Проводится факторный анализ априорных и апостиорных данных с целью отсеивания несущественных переменных в этих зависимостях.

Под факторным анализом понимается приближенная оценка параметров и коэффициентов уравнений в зависимости от выбранной меры точности совпадения экспериментальных и теоретических данных.

2. Проводятся эксперименты по определению реакции системы на воздействия по времени.

3. Строятся оценки данных характеристик объекта по времени.

4. Стоится математическая зависимость между выходными и входными переменными в динамике.

Эти операции методики построения математической модели, составляющие разделы теории САУ, известных как идентификация систем и устройств.

Под идентификацией понимается построение математической модели объектов по априорной и апостиорной информации и, в частности, по входным и выходным сигналам.

Наиболее распространены методы параметрической идентификации, когда структура математической модели уже задана, а требуется найти только ее параметры в соответствии с заданными критериями адекватности математической модели и объекта.

Определение математической модели динамики системы сводится к идентификации оператора L в выражении

Y(t) = L[X(t), (t), C(t)],

где Y(y₁, y₂,…, y_n), X(x₁, x₂,…, x_l) – векторы выходных и входных сигналов;

( ₁, ₂,…, _m) – вектор параметров системы;

С( с₁, с₂,…, с_k) – вектор параметров системы;

L – численный оператор.

На практике методы идентификации разработаны в основном для линейных детерминированных и стационарных стохастических систем.

Большое число этих методов базируется на уравнении Н. Винера

где - неизвестная весовая векторная функция системы (переходная функция на ступенчатое воздействие);

- взаимно – корреляционная вектор-функция стационарных случайных процессов на входе и выходе этой системы.

Перспективными и плодотворными являются методы идентификации оператора L, построенные на принципе настраиваемой модели.

В схемах с настраиваемой моделью структура модели предполагается известной, а настройке подвергаются параметры модели.

Основная идея принципа сводится к следующей схеме, представленной на рисунке 3.10.

Приведенная схема отражает общий случай, включает широкий набор вариантов, которые отличаются организацией критерия идентификации.

Выбор критерия – это сложная задача, во многом определяющая алгоритмы технической реализации схем.

Наиболее распространены выражения критериев в виде функционалов:

• интеграл квадрата ошибки

-интеграл от ошибки с весовой функцией времени

• интегральный критерий вида

Н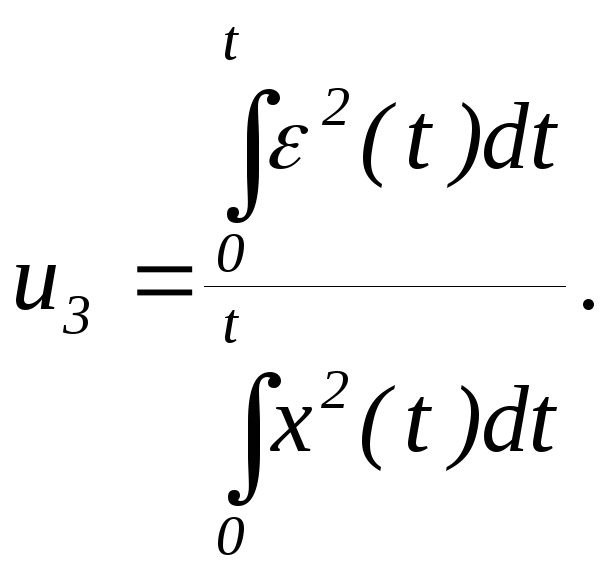аиболее целесообразным способом построения математической модели САУ являетсясочетание аналитических методов с численными.

При этом аналитическими методами строится возможно более полная математическая модель, а с помощью численных методов идентификации осуществляется количественная оценка параметров модели и обеспечивается адекватность ее реальному объекту.

При этом процедура построения математической модели состоит из трех этапов:

• вывод полой математической модели в аналитической форме на основе классических принципов;

• упрощение и преобразование математической модели в соответствии с назначением и особенностями модели;

• параметрическая идентификация упрощенной модели по результатам экспериментов и испытаний.