4. Линейные уравнения второго порядка.

Рассмотрим теперь важный класс уравнений вида

. (10)

Если , то данное уравнение называетсяоднородным. В противном случае, данное уравнение называется неоднородным.

Общее решение неоднородного уравнения имеет вид , где— общее решение соответствующего однородного уравнения: , а — некоторое частное решение исходного уравнения.

Будем рассматривать наиболее часто встречающиеся в практике случаи, когда коэффициенты ,,являются постоянными числами, а правая часть имеет простой (специальный) вид.

К таким уравнениям приводят многие физические задачи, решение которых, например, основано на втором законе механики , где— масса системы,— ускорение,— действующие силы.

Если, например, на некоторую систему действуют силы (сила, пропорциональная скорости движения) и(сила, восстанавливающая отклонение от положения равновесия), при этом внешнее возмущение описывается функцией, то учитывая, что, а, получаем

или ,

что, с точностью до обозначений, совпадает с общим видом линейных уравнений второго порядка (10).

Решение уравнения (10) ищем в виде . Для нахождениясоставляетсяхарактеристическое уравнение , находятся его корни ии, в зависимости от их значений, определяется. Правило нахождения укажем в таблице 3.Таблица 3

Характеристическое уравнение ,	Общее решение однородного уравнения
1. ,— действительные и различные
2. ,— действительные и равные
3. ,— комплексно сопряженные

При нахождении будем исходить из того, что правая часть уравнения имеет специальный вид: ;;;, гдеи— заданные многочлены в степени .

Например, — многочлен нулевой степени, — многочлен первой степени, — многочлен второй степени и так далее. Соответствующие значения для укажем в таблице 4.

Таблица 4

	, если число не является корнем характеристического уравнения и , если число является корнем характеристического уравнения.
,	, если число , не является корнем характеристического уравнения и , если число является корнем характеристического уравнения.
,	, если среди корней характеристического уравнения нет числа ; , если является однократным корнем характеристического уравнения; , если является двукратным корнем характеристического уравнения.
,	, если среди корней характеристического уравнения нет числа 0; , если число является однократным корнем характеристического уравнения; , если число является двукратным корнем характеристического уравнения.

В выражениях для содержится функция, которая представляет собой многочлен степени с неизвестными коэффициентами: . Задача состоит в том, чтобы найти эту функцию, т.е. найти неизвестные коэффициенты . Для этого нужно найти,, подставить значения,,в исходное уравнение и из сравнения левой и правой частей найти неизвестные коэффициенты.

Замечание. Если правая часть и — частное решение уравнения с правой частью,— частное решение уравнения с правой частью , то частное решение для уравнения с правой частью будет .

Пример 6. Найти общее решение уравнения (10), если ,,,.

Решение. При заданных значениях уравнение (10) примет вид

.

Обозначим искомое решение через . Тогда , где - общее решение уравнения . Составим характеристическое уравнение ,. Следовательно .

Найдем . Так как правая часть уравнения равна, то это случай 4 табл.4 и, частное решение было бы, если бы числа не было среди коней характеристического уравнения. Но, так как числовстречается среди коней характеристического уравнения один раз (), то. Найдем ,, подставим эти значения в данное уравнение и потребуем, чтобы оно обратилось в тождество

; ,

откуда .

Таким образом, и общее решение уравнения будет.

Если в начальный момент времени известныи, то можно найти частное решение уравнения (10), удовлетворяющее этим условиям, то есть решить, так называемую,задачу Коши.

Пример 7. Найти частное решение уравнения , удовлетворяющее начальным условиям .

Решение. Данное уравнение — это уравнение вида (10), при ,,,.

Найдем сначала общее решение данного уравнения.

Для этого решим соответствующее однородное уравнение:

. Следовательно .

Так как числа нет среди корней характеристического уравнения, то (случай 3, табл.2) частное решениеподбираем в таком же виде, как и правая часть,,. Подставляем эти значения в уравнение .

Следовательно, . Значит, - общее решение данного уравнения. Для нахождения частного решения, удовлетворяющего заданным начальным условиям, найдем:

. Так как и , то получаем

Подставляя эти значения в общее решение, найдем частное решение , удовлетворяющее заданным начальным условиям.

Пример 8. Найти частное решение уравнения , удовлетворяющее начальным условиям:.

Решение. Данное уравнение — это уравнение вида (10), при ,,,.

Решаем уравнение . Составляем характеристическое уравнение .

Следовательно, — общее решение уравнения без правой части. По виду правой частинаходим число, (случай 2, табл. 2). Такого числа среди корней характеристического уравнения нет, поэтому

; ;. Подставим эти значения в данное уравнение

или . Сравнивая слагаемые, содержащие и, получим

Поэтому

, — общее решение данного уравнения. Найдем

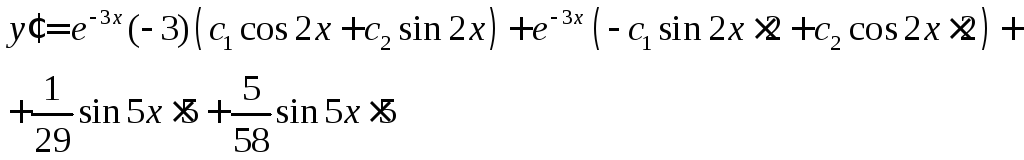
Учитывая начальные условия, найдем: , ,откуда . Подставляя эти значения в общее решение, получим

— частное решение исходного уравнения, удовлетворяющее заданным начальным условиям.

Физический смысл полученного решения (и предыдущих) в том, что это есть отклонение платформы от положения равновесия в любой момент времени. В частности, при получим

.