
- •Высшая математика
- •Часть 3
- •Составители: ст.Преп. Елена Николаевна Бесперстова
- •Рабочая программа
- •Рекомендуемая литература
- •Контрольная работа №7.
- •4.1-4.30.
- •Методические указания и примеры для выполнения контрольной работы № 7
- •1. Неопределенный интеграл
- •2. Основные методы интегрирования
- •3. Интегрирование рациональных дробей
- •4. Интегрирование некоторых иррациональных выражений
- •5. Интегрирование тригонометрических функций
- •6. Определенный интеграл
- •7. Несобственные интегралы.
- •8. Геометрические приложения определенного интеграла
- •Контрольная работа №8 Дифференциальные уравнения
- •Методические указания и примеры для выполнения контрольной работы №8
- •1. Дифференциальные уравнения
- •2. Дифференциальные уравнения первого порядка
- •2.1. Дифференциальные уравнения с разделяющимися переменными
- •2.2. Однородные уравнения первого порядка
- •2.3. Линейные уравнения первого порядка.
- •3. Дифференциальные уравнения высших порядков
- •4. Линейные уравнения второго порядка.
- •5. Системы дифференциальных уравнений
- •Контрольная работа №9
- •Методические указания и примеры для выполнения контрольной работы № 9
- •1. Кратные и криволинейные интегралы
- •2. Вычисление двойных интегралов
- •3. Вычисление тройных интегралов
- •4. Вычисление криволинейных интегралов
Методические указания и примеры для выполнения контрольной работы № 9
1. Кратные и криволинейные интегралы
1.1. Основные понятия и определения
Рассмотрим
некоторое измеримое множество точек
Е,
на котором определена непрерывная
функция
![]() .
Разобьем множествоЕ
произвольным образом на n
частей
.
Разобьем множествоЕ
произвольным образом на n
частей
![]() ,
причем, чтобы не вводить новых обозначений,
под
,
причем, чтобы не вводить новых обозначений,
под![]() будем понимать не только обозначение
соответствующей области, но и ее меру.
будем понимать не только обозначение
соответствующей области, но и ее меру.
Возьмем
точки
![]() ,
вычислим
,
вычислим![]() и составим сумму
и составим сумму
![]() .
.
Эту
сумму назовем интегральной
суммой
для функции
![]() на множествеЕ.
на множествеЕ.
Предел
интегральной суммы при
![]() ,
если он существует и не зависит ни от
способа разбиения множестваЕ
на части
,
если он существует и не зависит ни от
способа разбиения множестваЕ
на части
![]() ,
ни от выбора точек
,
ни от выбора точек![]() ,
называетсяинтегралом
от функции
,
называетсяинтегралом
от функции
![]() на
множестве
Е
и обозначается
на
множестве
Е
и обозначается
![]() .
Итак,
.
Итак,
![]() .
.
1.2. Определенный интеграл
Если
множество Е
представляет собой отрезок
![]() осиОх,
то
осиОх,
то
![]() ,
,![]() и мы получаем уже известное нам определение
определенного интеграла
и мы получаем уже известное нам определение
определенного интеграла
![]() .
.
1.3. Двойной интеграл.
Если
множество Е
— некоторая область D
в плоскости Oxy,
то
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() и
и![]() — интегральная сумма для функции
— интегральная сумма для функции![]() в областиD,
а ее предел (если он существует), при
в областиD,
а ее предел (если он существует), при
![]() ,
называетсядвойным
интегралом
от функции
,
называетсядвойным
интегралом
от функции
![]() на областиD
и обозначается
на областиD
и обозначается
![]() .
.
Итак, ![]() .
.
Геометрический смысл интегральной суммы, стоящей под знаком предела — сумма объемов «столбиков», один из которых показан на рис. 6.

рис. 6
1.4. Тройной интеграл.
Если
множество Е
— некоторая пространственная область
V,
то
![]() ,
,![]() ,
,![]() и
и![]() — интегральная сумма для функции
— интегральная сумма для функции![]() в областиV,
а ее предел (если он существует), при
в областиV,
а ее предел (если он существует), при
![]() ,
называетсятройным
интегралом
от функции
,
называетсятройным
интегралом
от функции
![]() на областиV
и обозначается
на областиV
и обозначается
![]() .
.
Итак,
![]() .
.
Аналогичным образом определяется любой n-кратный интеграл.
Замечание.
Если
функции
![]() ,
,![]() ,
,![]() ,
… непрерывны в соответствующих областях,
то интегралы от этих функцийсуществуют.
,
… непрерывны в соответствующих областях,
то интегралы от этих функцийсуществуют.
Геометрический
смысл определенного интеграла уже
известен. Геометрический смысл двойного
интеграла — объем
цилиндрического тела, в основании
которого лежит область D,
сверху — поверхность
![]() ,
а с боков — цилиндрическая поверхность
с образующими, параллельными осиOz
(рис.6). Интегралы более высокой кратности
геометрического смысла в общем случае
не имеют.
,
а с боков — цилиндрическая поверхность
с образующими, параллельными осиOz
(рис.6). Интегралы более высокой кратности
геометрического смысла в общем случае
не имеют.
Физический смысл всех рассмотренных интегралов — масса соответствующей области интегрирования, для которой подынтегральная функция является плотностью распределения масс.
Свойства кратных интегралов аналогичны известным свойствам определенного интеграла.
С
помощью кратных интегралов можно
вычислять площади, объемы, находить
статистические моменты и моменты
инерции, координаты центров тяжести
различных тел и решать другие задачи.
В частности, площади плоских областей
можно находить по формуле
![]() ,
а объемы пространственных тел по формуле
,
а объемы пространственных тел по формуле![]() .
.
1.5. Криволинейный интеграл
Рассмотрим
случай, когда множество Е
— некоторый участок АВ
кривой L,
лежащий в плоскости Oxy,
в каждой точке которой определены и
непрерывны функции
![]() и
и![]() .
По аналогии с предыдущим, составим
интегральную сумму
.
По аналогии с предыдущим, составим
интегральную сумму
![]() ,
,
где
точка
![]() .
.
Предел
этой суммы, при
![]() и
и![]() ,
если он существует, называетсякриволинейным
интегралом по координатам по
кривой L
и обозначается
,
если он существует, называетсякриволинейным
интегралом по координатам по
кривой L
и обозначается
![]() .
.
Таким образом,
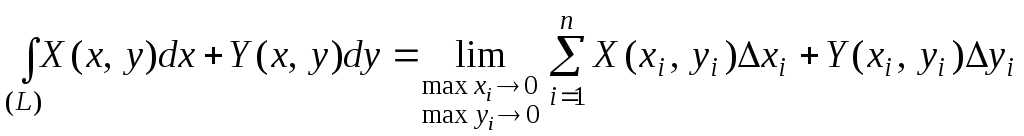
Из свойств криволинейного интеграла отметим только одно: при изменении направления интегрирования криволинейный интеграл меняет знак.
Если
![]() и
и![]() являются координатами вектора
являются координатами вектора![]() ,
определенного в точках кривойL,
то этот вектор задает векторное (силовое)
поле над кривой L
и тогда криволинейный интеграл определяет
работу,
совершаемую вектором
,
определенного в точках кривойL,
то этот вектор задает векторное (силовое)
поле над кривой L
и тогда криволинейный интеграл определяет
работу,
совершаемую вектором
![]() на участке кривойL
от точки A
до точки B.
Если кривая L
замкнута, то указанная работа называется
циркуляцией
векторного поля.
на участке кривойL
от точки A
до точки B.
Если кривая L
замкнута, то указанная работа называется
циркуляцией
векторного поля.
Аналогичным образом определяется криволинейный интеграл по пространственной кривой.
