7. Несобственные интегралы.

Несобственные интегралы первого рода.

Если функция непрерывна на промежутке, то интегралназываетсянесобственным интегралом первого рода.

По определению =.

При этом, если предел, стоящий справа, существует (т.е. равен некоторому действительному числу), то несобственный интеграл называется сходящимся. Если же предел, стоящий справа, равен или не существует вообще, то несобственный интеграл называетсярасходящимся.

Аналогичным образом определяется несобственный интеграл от функции непрерывной в интервале:

, где а — произвольное действительное число.

При этом несобственный интеграл будет сходящимся, если существуют оба предела, стоящие справа в этой формуле.

Пример 18. Вычислить несобственный интеграл или доказать его расходимость.

Решение.

Таким образом, несобственный интеграл равен , т.е. он сходится.

Несобственные интегралы второго рода.

Пусть функция непрерывна на отрезке, а в точкеимеет бесконечный разрыв. Тогда интеграл от этой функции на отрезке, где- любое действительное число,называетсянесобственным интегралом второго рода и вычисляется по формуле

.

Если функция имеет разрыв в точке, то несобственный интеграл от этой функции на отрезкевычисляется по формуле

.

Если функция имеет бесконечный разрыв внутри отрезкав некоторой точке, то несобственный интеграл будет равен

.

Если пределы, стоящие справа, равны действительным числам, то несобственный интеграл является сходящимся, а если хотя бы один предел, стоящий справа, равен или не существует вообще, то несобственный интеграл является расходящимся.

Пример 19. Вычислить интеграл или доказать его расходимость.

Решение.

рис. 2

Так как оба предела стремятся к бесконечности, то они не существуют и поэтому, несобственный интеграл расходится.

8. Геометрические приложения определенного интеграла

1) Площадь области, ограниченной непрерывной кривой (), отрезкомосиOX и прямыми , вычисляется по формуле

.

Если на всем отрезкеили на его части, то соответствующая часть площади корректируется знаком «минус».

Если функция задана параметрическими уравнениями ,, где, то площадь соответствующей криволинейной трапеции вычисляется по формуле

.

Площадь области, ограниченной кривой, заданной уравнением в полярной системе координат и двумя лучамии, находится по формуле

.

2) Длина дуги плоской кривой, заданной уравнением ,, гдеи— непрерывные на отрезкефункции, находится по формуле

.

Если кривая задана параметрическими уравнениями ,,, гденепрерывны на указанном отрезке вместе со своими производными, то длина соответствующей дуги равна

.

Для кривой, определенной в полярной системе координат уравнением ,, длина дуги находится по формуле

.

3) Объем тела, полученного при вращении непрерывной кривой ,, вокруг осиOX равен

.

Если кривая вращается вокруг оси OY, причем , то

.

Пример 20. Найти площадь фигуры, ограниченной линиями ,.

Решение. Первое уравнение определяет на плоскости прямую линию, второе – гиперболу (рис.3).

рис. 3

Найдем их точки пересечения

Пример 21. Вычислить площадь области, ограниченной кривой, уравнение которой в полярной системе координат имеет вид ,.

Решение.

Для построения кривой составим таблицу значений функции:

Таблица 2

	0	15	30	45	60	75	90	105	120	135	150	165	180
	3	2,55	1,5	0	-	-	-	-	-	0	1,5	2,55	3

Для значениябудут повторяться в силу периодичности функции. Строим кривую по точкам (нижняя часть кривой симметрично достраивается) (рис.4)

рис. 4

Заметим, что построенная фигура состоит из четырех равных частей, поэтому

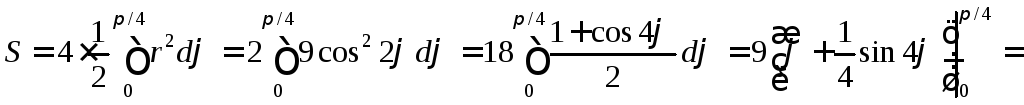
(кв.ед.)