1.5. Інтегрування раціональних дробів

Відношення двох многочленівівідповідноm-го і n-го степеня називається дробно-раціональною функцією або раціональним дробом.

Раціональний дріб називається правильним, якщо . Якщо ж, то раціональний дріб називається неправильним. В цьому випадку розділившинаодержимо:

(1.10)

де і- многочлени відповідноm-n-го та k- го степенів, причому , тобто дріб- правильний.

Знаменник розкладається на добуток лінійних і квадратних множників, перші з яких лінійні відповідають дійсним кореням, а другі (квадратні) – комплексно спряженим кореням. Кратні корені характеризуються відповідними степенями цих множників.

Елементарними раціональними дробами називаються такі правильні раціональні дроби.

а) ; б);; в); г);

де А, а, М, N, p, q – дійсні числа, а тричлен не має дійсних коренів.

Отже, правильний раціональний дріб, у якого тобтомає дійсний корінь кратностіі два комплексно спряжені корені кратності, розкладається на суму елементарних дробів так:

(1.11)

Якщо має більше дійсних і комплексно-спряжених коренів, то розклад (1.11) відповідно розширюється.

Нехай потрібно знайти інтеграл

(1.12)

Згідно з (1.10) інтеграл виду (1.12) запишеться так

(1.13)

Інтеграл від многочлена обчислюється за табличним інтегралом 1, а інтеграл від правильного дробу, згідно з (1.11) зводиться до обчислення інтегралів від елементарних раціональних дробів.

Розглянемо ці інтеграли. Скористаємось наведеними вище перетвореннями диференціала і табличними інтегралами 2 і 1. Тоді для елементарних дробів а) і б) будемо мати:

І. ;

ІІ. ;

ІІІ. Обчислення інтеграла від елементарного дробу в) базується на виділенні у знаменнику дробу ( в квадратному тричлені) повного квадрату, тобто

В результаті одержимо:

^(1.14)

Далі можливі такі випадки: якщо т=0, тоді при інтеграл зводиться до інтегралу 11, а при- до інтегралу 12. Якщо ж, тоді інтеграл (1.14) зводиться до інтегралів 13 і 11, або до інтегралів 13 і 12. Як це робиться , покажемо на конкретних прикладах.

Приклад 1.

Приклад 2.

;

Приклад 3.

Приклад 4.

Зауваження. Перетворення, які були зроблені у чисельниках прикладів 3, 4 пов’язані із виділенням у них похідних або диференціалів знаменників та зведенням їх до інтеграла 13.

IV. Інтеграл виду:

де

підстановкою зводиться до суми двох інтегралів

, де ;

Перший із цих інтегралів обчислюється згідно з інтегралом 1, а другий за рекурентною формулою.

(1.15)

Приклад.

=

.

Питання інтегрування неправильного раціонального дробу розглянемо на такому прикладі:

Виділимо цілу частину дробу

=.

Розкладемо правильний дріб на елементарні і зведемо вираз до спільного знаменника. .

Прирівняємо коефіцієнти при невідомих і розв’яжемо систему рівнянь.

В результаті:

=.

1.6. Інтегрування простих ірраціональностей

Функція називається раціональною від змінних, якщо над цими змінними і дійсними числами виконується скінчене число операцій додавання, віднімання, множення і ділення. Змінніможуть бути і функціями. Наприклад, функціяє раціональною функцією відносно функції, тобто

.

Розглянемо способи інтегрування таких функцій.

1. Інтеграл раціоналізується підстановкою.

Звідси . Отже

Приклад. Знайти інтеграл.

=

=

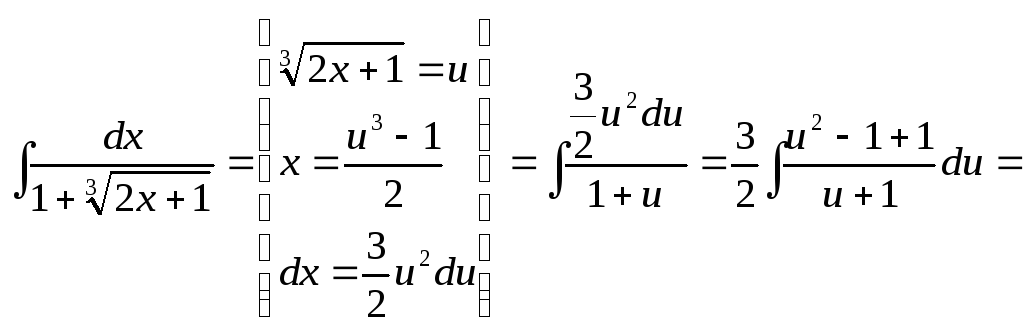
2. Інтеграл більш загального виду

раціоналізується підстановкою .

Звідси ,, або. Отже

.

Приклад. Знайти інтеграл.

+ .

3. Інтеграл виду знаходиться підстановкою,

; . В залежності від значеньa,b,c, він зводиться до одного із табличних інтегралів 9 або 10.

Приклад. Знайти інтеграл.

=

=