
- •М.Д. Бабич, с.І. Куприков
- •1. Невизначений інтеграл
- •1.1. Первісна функція. Невизначений інтеграл.
- •1.2. Основні властивості невизначеного інтеграла
- •1.3. Таблиця основних невизначених інтегралів
- •Покажемо на прикладах, що наведені табличні інтеграли будуть вірні, коли - незалежній змінній і коли- диференційовній функції відx.
- •1.4. Основні методи інтегрування
- •1.5. Інтегрування раціональних дробів
- •1.6. Інтегрування простих ірраціональностей
- •1.7. Інтегрування тригонометричних функцій
- •1.8. Інтегрування деяких трансцендентних функцій
- •2. Визначений інтеграл
- •2.1. Визначений інтеграл як границя інтегральної суми
- •2.2. Обчислення визначеного інтеграла. Формула Ньютона-Лейбніца.
- •2.3. Основні властивості визначеного інтеграла.
- •2.4. Методи обчислення визначених інтегралів
- •2.5. Застосування визначеного інтеграла
- •3. Функції двох змінних
- •3.1. Поняття функції двох змінних та їх геометричне зображення
- •3.2. Локальні екстремуми функції двох змінних
- •Дослідимо цю функцію всередині трикутника
- •4. Диференціальні рівняння
- •4.1. Основні поняття. Задача Коші.
- •4.2. Диференціальні рівняння першого порядку з відокремлюваними змінними
- •4.3. Лінійні диференціальні рівняння. Однорідні диференціальні рівняння
- •4.4. Диференціальні рівняння другого порядку
- •Диференціальні рівняння другого порядку, що допускають пониження порядку
- •4.5. Лінійні диференціальні рівняння другого порядку.
- •4.6. Лінійні однорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •4.7. Лінійні неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •5. Числові та функціональні ряди
- •5.1. Числові ряди. Ознаки збіжності
- •5.2. Знакозмінні ряди
- •5.3. Функціональні ряди
- •5.4. Степеневі ряди. Радіус збіжності
- •5.5. Ряди Тейлора і Маклорена
- •Контрольна робота № 2
- •Рекомендована література
1.7. Інтегрування тригонометричних функцій
Важливе значення у прикладних питаннях деяких природничих наук мають інтеграли.
|
|
(1.16) |
де m і n цілі невід’ємні числа.
Тут можливі такі випадки:
а) хоча
б один із показників m
або
n непарне число. В цьому
випадку інтеграл (1.16) знаходиться
підстановкою
![]() ,
якщоn-непарне,
і підстановкою
,
якщоn-непарне,
і підстановкою
![]() ,
якщоm-непарне.
Якщо ж m і
n обидва непарні, то
можна брати будь-яку з цих підстановок.
,
якщоm-непарне.
Якщо ж m і
n обидва непарні, то
можна брати будь-яку з цих підстановок.
Приклад. Знайти інтеграл.
![]()
 =
=![]() .
.
б) обидва показники m і n парні числа. В цьому випадку інтеграл (1.16) береться за допомогою тригонометричних тотожностей пониження степеня, а саме, формул подвійного аргументу:
![]() ,
,
![]() ,
,![]()
Приклад. Знайти інтеграл.
![]()
![]()
![]()
![]()
![]() .
.
В теорії рядів Фур’є важливу роль відіграють інтеграли виду:
|
|
(1.17) |
Всі ці інтеграли обчислюються на основі наступних тригонометричних формул:
![]() ,
,
![]()
![]() .
.
Приклад. Знайти інтеграл.
![]()
![]()
![]() .
.
1.8. Інтегрування деяких трансцендентних функцій
Вище ми
розглядали інтеграли від раціональних
функцій
![]() ,
де змінні
,
де змінні![]() були раціональні та ірраціональні
вирази або функції. Важливим є клас
інтегралів від раціональних функцій,
змінними в яких є деякі трансцендентні
функції. Розглянемо такі інтеграли.
були раціональні та ірраціональні
вирази або функції. Важливим є клас
інтегралів від раціональних функцій,
змінними в яких є деякі трансцендентні
функції. Розглянемо такі інтеграли.
1.
![]() .
Цей інтеграл раціоналізується до
алгебраїчного виду підстановкою
.
Цей інтеграл раціоналізується до
алгебраїчного виду підстановкою![]() .
Звідси
.
Звідси![]() .
Таким чином
.
Таким чином![]() .
.
Приклад. Знайти інтеграл.

![]()
![]() .
.
2. Інтеграл
![]() -
зводиться до раціонального алгебраїчного
виду підстановкою
-
зводиться до раціонального алгебраїчного
виду підстановкою![]() .
Звідси
.
Звідси![]() ,
,![]() ,
,![]()
![]() .
В результаті одержується
.
В результаті одержується![]() .
.
Приклад. Знайти інтеграл.

=![]()
![]() .
.
Зауваження.
Підстановка
![]() дає можливість звести до раціонального
алгебраїчного виду інтеграл (1.16) у тому
випадку, коли хоча б один, або обидва
показникиm і
n
від’ємні.
дає можливість звести до раціонального
алгебраїчного виду інтеграл (1.16) у тому
випадку, коли хоча б один, або обидва
показникиm і
n
від’ємні.
Приклад. Знайти інтеграл.

![]() .
.
Інтеграл
виду
![]() зводиться до раціонального алгебраїчного
виду універсальною підстановкою
зводиться до раціонального алгебраїчного
виду універсальною підстановкою![]()
![]() . Звідси
. Звідси![]() ,
,![]() ,
,![]() ,
,![]() .
.
Отже
![]() .
.
Назва
універсальна підстановка говорить про
те, що вона може бути застосована при
знаходженні інтеграла від будь-яких
співвідношень тригонометричних функцій
![]() і
і![]() .
Однако, найбільш ефективною вона є в
тих випадках, коли функції
.
Однако, найбільш ефективною вона є в
тих випадках, коли функції![]() і
і![]() мають перші степені і представлені у
вигляді суми чи різниці. Застосування
цієї підстановки до випадків, коли
мають перші степені і представлені у
вигляді суми чи різниці. Застосування
цієї підстановки до випадків, коли![]() і
і![]() мають парні степені приводить до
раціональних дробів з високими степенями.
Тому, в таких випадках краще застосовувати
підстановку
мають парні степені приводить до
раціональних дробів з високими степенями.
Тому, в таких випадках краще застосовувати
підстановку![]() ,
або якусь іншу.
,
або якусь іншу.
Приклад. Знайти інтеграл.

![]()

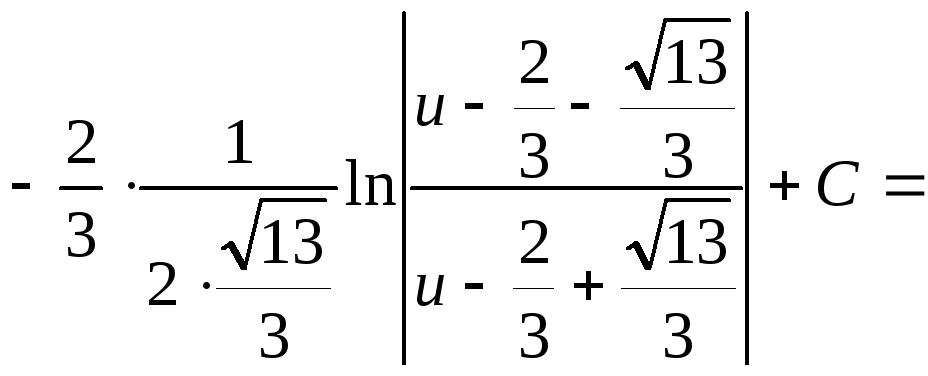
 .
.
4. Інтеграл
виду
![]() підстановкою
підстановкою![]() зводиться до одного із таких інтегралів:
зводиться до одного із таких інтегралів:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() які в свою чергу, підстановками відповідно
які в свою чергу, підстановками відповідно![]() ,
,![]() ,
,![]() зводиться до інтегралів виду
зводиться до інтегралів виду![]() .
.
Приклад. Знайти інтеграл.
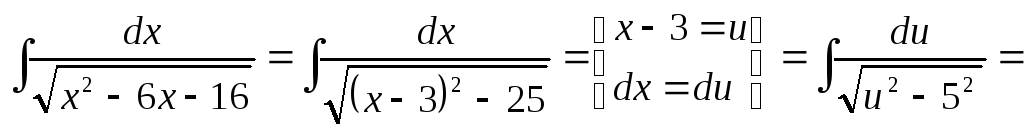



![]()
2. Визначений інтеграл
2.1. Визначений інтеграл як границя інтегральної суми
Нехай
функція
![]() неперервна на відрізку
неперервна на відрізку![]() причому
причому![]() і
і![]() .
Фігура , що обмежена кривою
.
Фігура , що обмежена кривою![]() ,
віссю ОХ та ординатами
,
віссю ОХ та ординатами![]() називається криволінійною трапецією
називається криволінійною трапецією![]() .
.

Нехай
S-площа
![]() (рис 1). Розіб’ємо відрізок
(рис 1). Розіб’ємо відрізок![]() нап-
довільних частин точками
нап-
довільних частин точками
![]() і в точках
і в точках![]() проведемо ординати до перетину із
кривою. Тоді криволінійна трапеція
розіб’ється нап
полосок, кожну з яких можна вважати за
прямокутник з основою
проведемо ординати до перетину із
кривою. Тоді криволінійна трапеція
розіб’ється нап
полосок, кожну з яких можна вважати за
прямокутник з основою
![]() .
У кожному із проміжків
.
У кожному із проміжків![]() візьмемо точку
візьмемо точку![]() ,
а значення
,
а значення![]() приймемо за висоту відповідного
прямокутника. Тоді площа такого
прямокутника буде рівна
приймемо за висоту відповідного
прямокутника. Тоді площа такого
прямокутника буде рівна![]()
![]()
![]() ,
а площа ступінчатої фігури, що складається
із
,
а площа ступінчатої фігури, що складається
із![]() таких прямокутників, буде
таких прямокутників, буде
![]() ,
або
,
або
|
|
(2.1) |
де
![]() - означає знак сумування.
- означає знак сумування.
Сума
![]() із (2.1) називається інтегральною сумою
для функції
із (2.1) називається інтегральною сумою
для функції![]() .
Очевидно, що при
.
Очевидно, що при![]() і
і![]() всі прямокутники
всі прямокутники![]() границі будуть прямувати до ординат
функції
границі будуть прямувати до ординат
функції![]() ,
а сума
,
а сума![]() - площі
- площі![]() .
Отже, має місце твердження.
.
Отже, має місце твердження.
Якщо
при
![]() і
і![]() існує скінченна границя інтегральної
суми
існує скінченна границя інтегральної
суми![]() (2.1), яка не залежить від розбиття відрізка
та вибору точок
(2.1), яка не залежить від розбиття відрізка
та вибору точок![]() ,
тоця
границя називається
визначеним інтегралом функції
,
тоця
границя називається
визначеним інтегралом функції
![]() на відрізку
на відрізку
![]() ,
тобто
,
тобто
![]() .
.
Але,
оскільки
![]() ,
то звідси випливаєгеометричний
зміст визначеного інтеграла,
а саме: визначений інтеграл від невід‘ємної
функції на відрізку
,
то звідси випливаєгеометричний
зміст визначеного інтеграла,
а саме: визначений інтеграл від невід‘ємної
функції на відрізку
![]() дорівнює площі відповідної криволінійної
трапеції (в даному випадку
дорівнює площі відповідної криволінійної
трапеції (в даному випадку![]() ),
тобто
),
тобто
|
|
(2.2) |
