
- •Лекция 2. Понятие кривой. Гладкие кривые. Канонический репер. Формулы Серре-Френе §2. Понятие кривой
- •§3. Гладкие кривые
- •§4. Касательная к кривой
- •§5. Длина кривой
- •§6. Канонический репер
- •§7. Формулы Серре-Френе
- •Лекция 3. Понятие поверхности. Гладкие поверхности. Координатная сеть на поверхности. Касательная плоскость и нормаль к поверхности §8. Векторная функция двух скалярных аргументов
- •§9. Понятие поверхности
- •§10. Кривые на поверхности
- •§11. Касательная плоскость и нормаль к поверхности
- •Лекция 4. Первая и вторая квадратичная форма поверхности §12. Первая квадратичная форма поверхности
- •§13. Вторая квадратичная форма поверхности. Кривизна линий на поверхности
- •§14. Индикатриса Дюпена
- •Лекция 5. Понятие внутренней геометрии поверхностей §15. Главные направления на поверхности. Полная и средняя кривизна поверхности. Формула Эйлера
- •§16. Внутренняя геометрия поверхности
- •Раздел IX. Основания геометрии
- •Лекция 1. Род структур. Основные математические структуры курса геометрии §1. Род структур
- •§2. Основные математические структуры курса геометрии
- •Лекция 2. Теория рода структур. Модель системы аксиом. Основные свойства системы аксиом §3. Теория рода структур
- •§4. Модель системы аксиом
- •§5. Основные свойства системы аксиом
- •Лекция 3. Основные этапы истории развития геометрии. «Начала» Евклида. Проблема пятого постулата и ее решение §6. Основные этапы истории развития геометрии. «Начала» Евклида
- •Лекция 4. Система аксиом Гильберта евклидовой геометрии §7. Обзор аксиоматики Гильберта евклидовой геометрии
- •I. Аксиомы принадлежности.
- •II. Аксиомы порядка.
- •III. Аксиомы конгруэнтности.
- •IV. Аксиомы непрерывности.
- •Лекция 5. Аксиоматика плоскости Лобачевского. Элементарные теоремы планиметрии Лобачевского §8. Независимость аксиомы параллельных от остальных аксиом евклидовой геометрии
- •§9. Элементарные теоремы геометрии Лобачевского
- •§10. Взаимное расположение прямых на плоскости Лобачевского
- •Лекция 6. Определение длины отрезка. Понятие площади плоской фигуры.
- •§11. Длина отрезка как результат процесса измерения
- •§12. Определение длины отрезка на основе расстояния между точками
- •§13. Аксиоматическое определение длины отрезка
- •§14. Площадь многоугольной фигуры
- •§15. Расширение класса квадрируемых фигур
- •Лекция 7. Величина и её измерение §16. Измерение объемов многогранных тел
- •§17. Расширение класса кубируемых фигур
- •§18. Понятие величины и её измерение
- •Литература
III. Аксиомы конгруэнтности.
Если даны отрезок
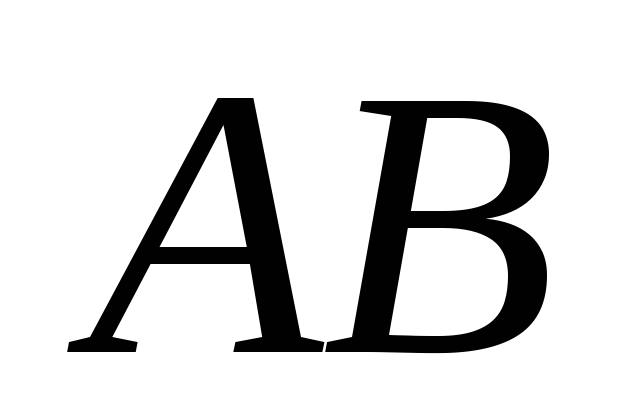 и луч
и луч ,
то существует точка
,
то существует точка ,
принадлежащая лучу, такая, что отрезок
,
принадлежащая лучу, такая, что отрезок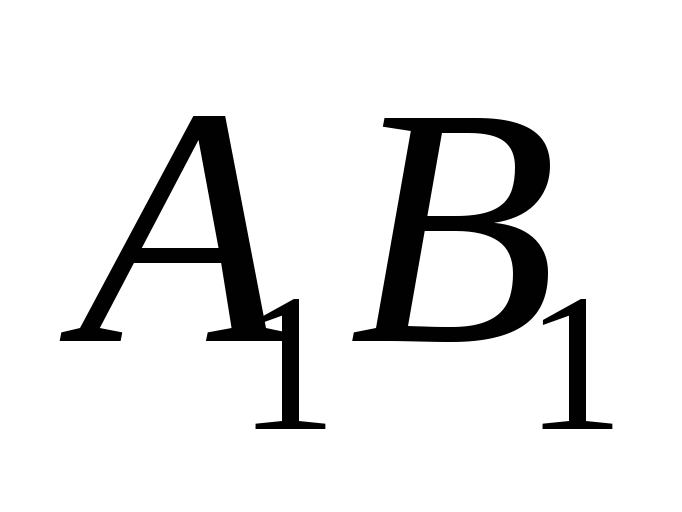 конгруэнтен отрезку
конгруэнтен отрезку .
Единственность точки
.
Единственность точки можно доказать.
можно доказать.Если отрезки и
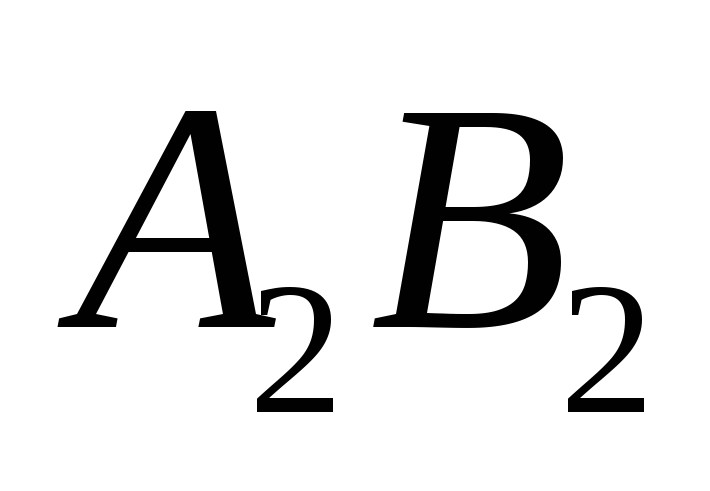 конгруэнтны одному и тому же отрезку
конгруэнтны одному и тому же отрезку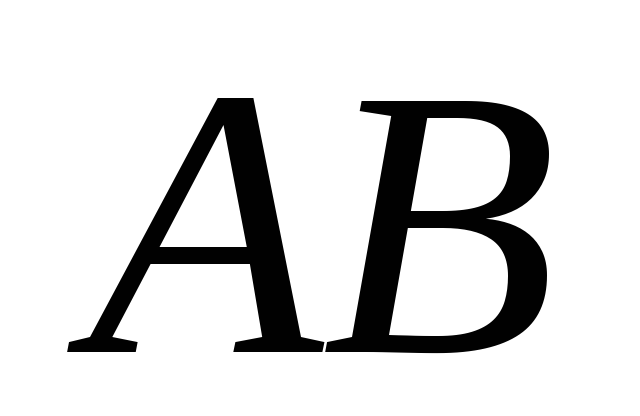 ,
то отрезок
,
то отрезок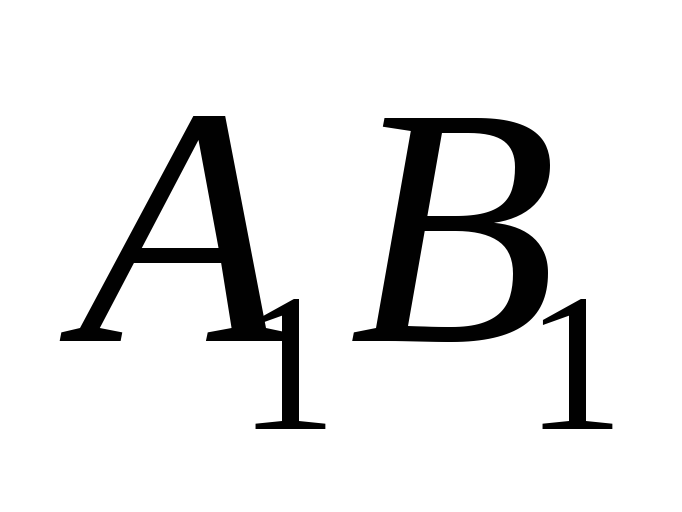 конгруэнтен отрезку
конгруэнтен отрезку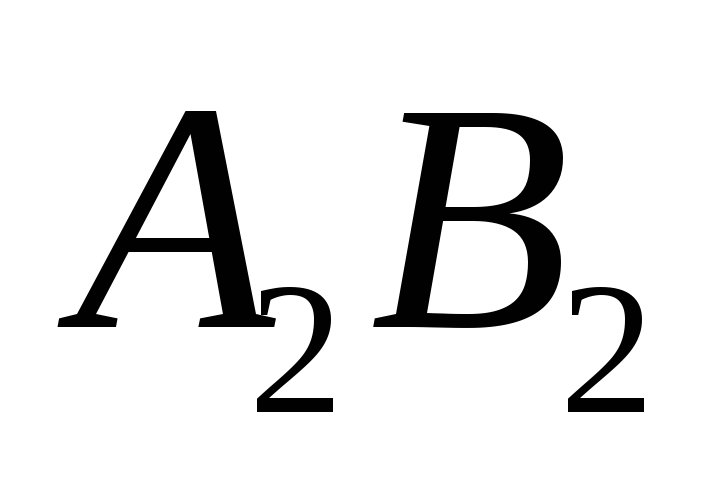 .
.Если точка
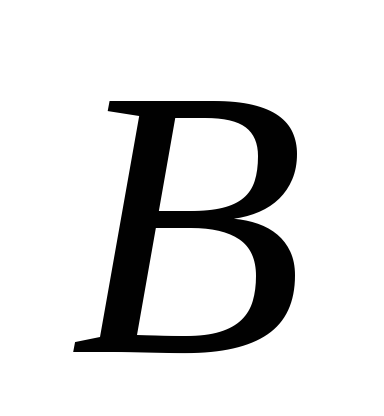 лежит между точками
лежит между точками и
и ,
а
,
а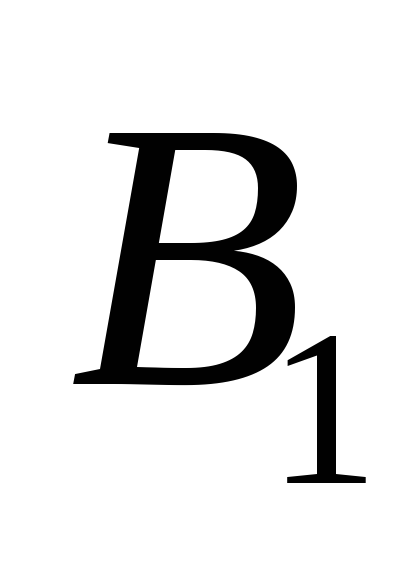 лежит между точками
лежит между точками и
и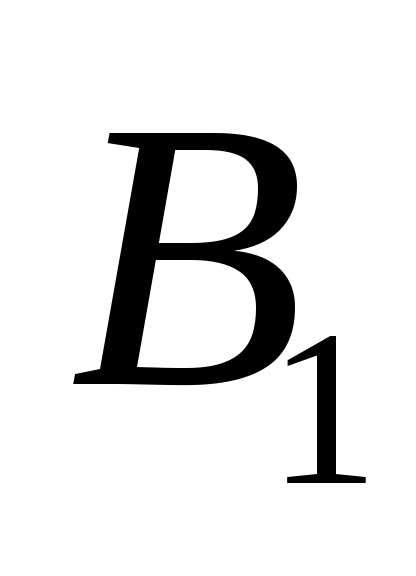 ,
и отрезок
,
и отрезок конгруэнтен отрезку
конгруэнтен отрезку ,
а отрезок
,
а отрезок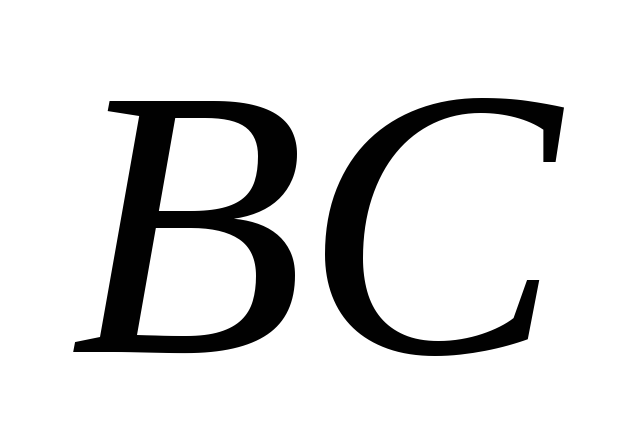 конгруэнтен отрезку
конгруэнтен отрезку ,
то отрезки
,
то отрезки и
и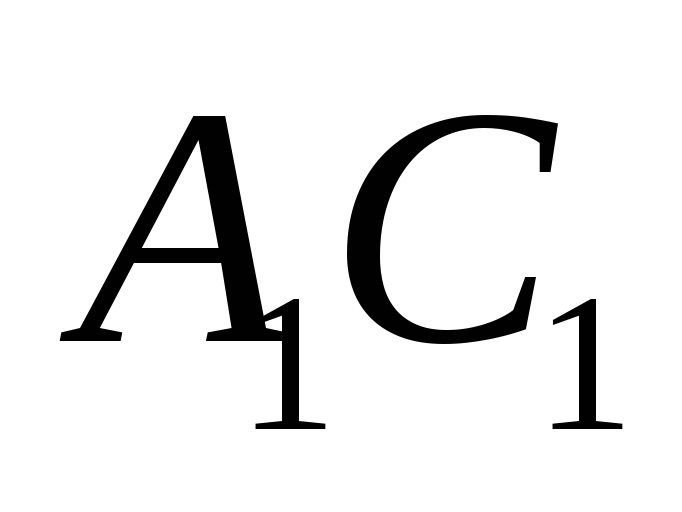 конгруэнтны.
конгруэнтны.Пусть даны
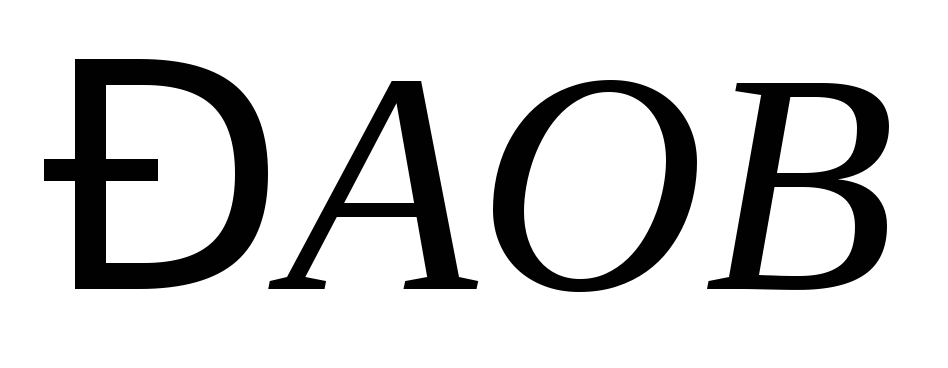 ,
луч
,
луч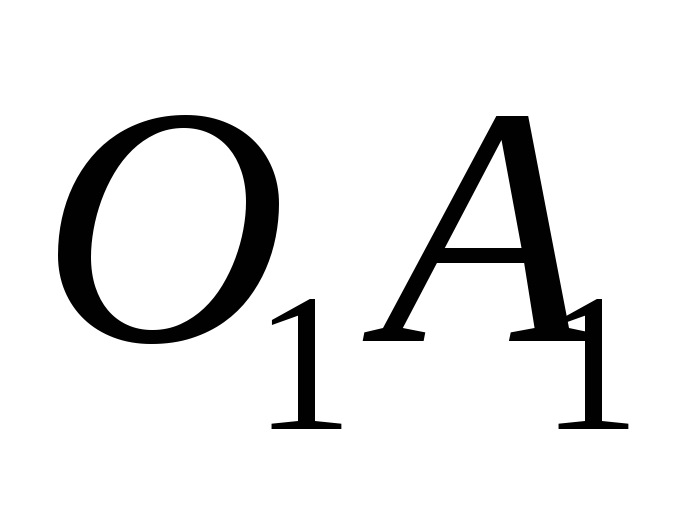 и полуплоскость
и полуплоскость с границей
с границей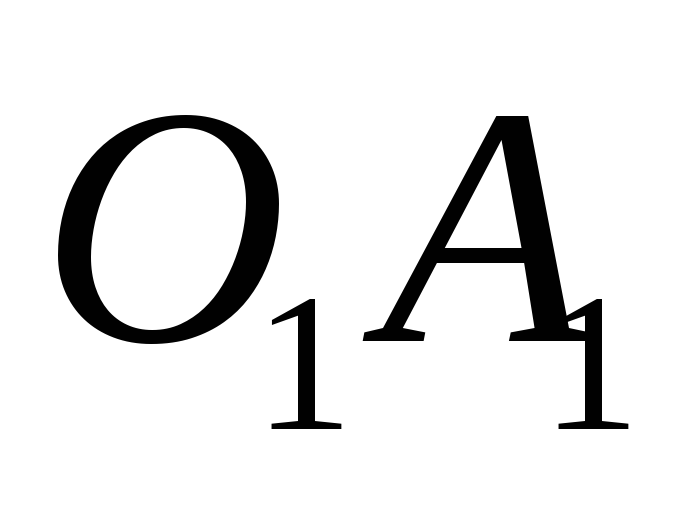 .
Тогда в полуплоскости
.
Тогда в полуплоскости существует единственный луч
существует единственный луч ,
такой, что
,
такой, что ,
кроме того
,
кроме того .
.Если две стороны и угол между ними одного треугольника конгруэнтны соответственно сторонам и углу между ними другого треугольника, то конгруэнтны соответственные углы при других вершинах треугольника.
Основываясь на аксиомах первых трех групп, можно доказать:
Отношение конгруэнтности отрезков является отношением эквивалентности на множестве отрезков.
В равнобедренном треугольнике углы при основании конгруэнтны.
Считая конгруэнтными два треугольника, у которых соответственные стороны и соответственные углы конгруэнтны, можно доказать три признака конгруэнтности треугольников.
Отношение конгруэнтности углов является отношением эквивалентности на множестве углов.
Введя понятие смежных углов, прямого угла, как угла, конгруэнтного смежному с ним, можно доказать, что все прямые углы конгруэнтны.
Введя сравнение отрезков и углов, можно доказать, что внешний угол треугольника больше каждого угла треугольника, не смежного с ним.
В треугольнике против большей стороны лежит больший угол, и наоборот.
Определив середину отрезка и биссектрису угла, можно доказать, что любой отрезок имеет единственную середину, любой угол имеет единственную биссектрису.
Определив сумму и разность отрезков, можно доказать, что во всяком треугольнике каждая сторона меньше суммы и больше разности двух других сторон.
В прямоугольном треугольнике гипотенуза больше каждого катета.
Три медианы (соответственно три высоты, три биссектрисы) треугольника пересекаются в одной точке.
IV. Аксиомы непрерывности.
Здесь мы приводим изложение, принятое в учебной литературе, отличное от схемы Гильберта.
4.1.
(Аксиома
Архимеда).
Пусть
![]() и
и![]() – какие-либо два отрезка. На луче
– какие-либо два отрезка. На луче![]() существует конечное множество точек
существует конечное множество точек![]() .таких,
что выполняются условия:
.таких,
что выполняются условия:
а) ;
б) отрезки
![]() конгруэнтны отрезку
конгруэнтны отрезку![]() ;
;
в) точка
![]() лежит между
лежит между![]() и
и![]() .
.
4.2.
(Аксиома
Кантора).
Пусть на прямой
![]() дана бесконечная последовательность
отрезков
дана бесконечная последовательность
отрезков![]() ,
удовлетворяющая условиям:
,
удовлетворяющая условиям:
а) каждый последующий отрезок содержится в предыдущем;
б) для
любого наперед заданного отрезка
![]() найдется
найдется![]() ,
что
,
что![]() .
.
Тогда
существует точка , принадлежащая каждому
из отрезков последовательности
![]() (можно доказать, что такая точка
единственная).
(можно доказать, что такая точка
единственная).
Можно доказать, что аксиомы 4.1 и 4.2 при сохранении аксиом I и III групп эквивалентны предложению Дедекинда:
Пусть
точки отрезка
![]() разбиты на два класса
разбиты на два класса![]() и
и![]() ,
то есть
,
то есть![]() и
и![]() ,
так что выполняются условия:
,
так что выполняются условия:
точка
 принадлежит классу
принадлежит классу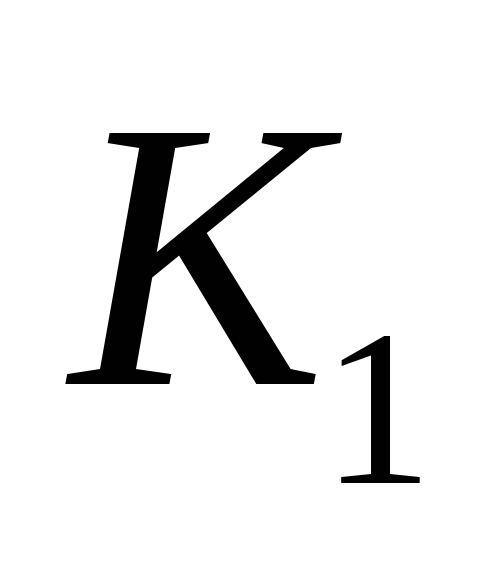 ,
точка
,
точка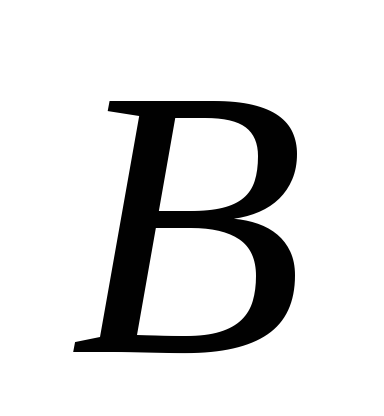 – классу
– классу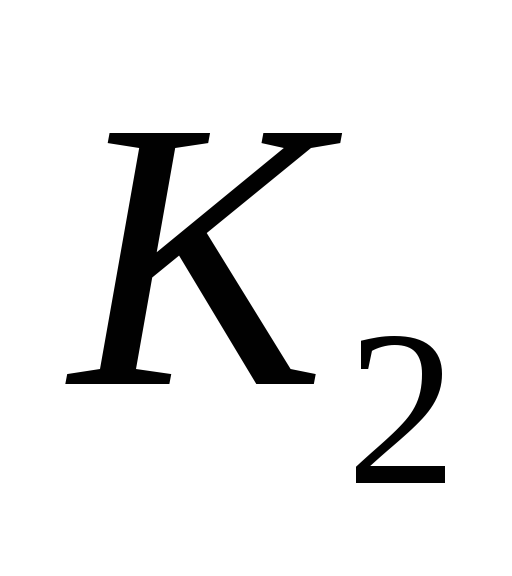 ;
классы содержат точки, отличные от и
;
классы содержат точки, отличные от и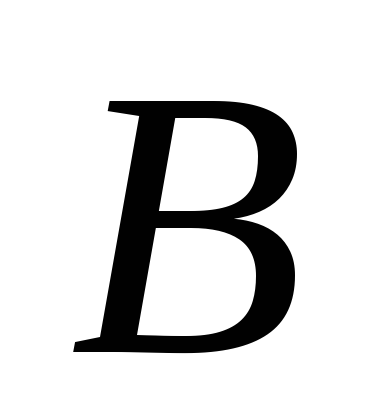 ;
;каждая точка
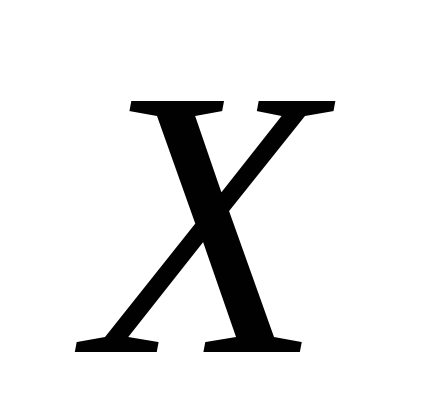 класса
класса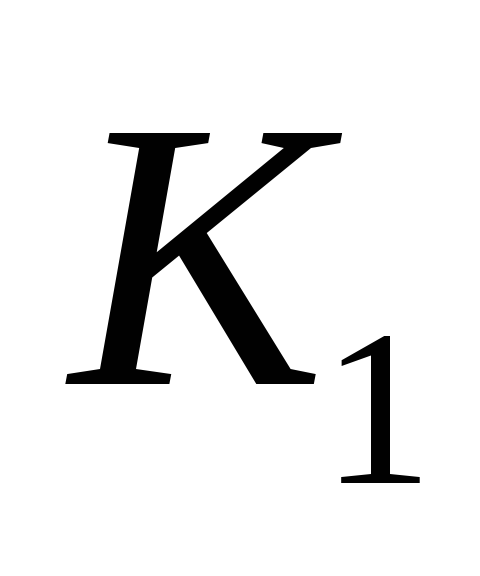 ,
отличная от
,
отличная от ,
лежит между
,
лежит между и любой точкой
и любой точкой второго класса
второго класса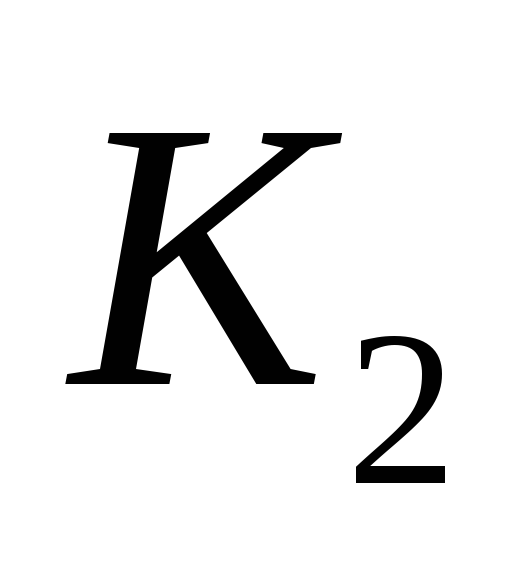 .
.
Тогда
существует единственная точка
![]() ,
такая, что точки
,
такая, что точки![]() ,
лежащие между
,
лежащие между
![]() и
и![]() ,
принадлежат классу
,
принадлежат классу![]() ,
а точки
,
а точки![]() ,
лежащие между
,
лежащие между![]() и
и![]() ,
– классу
,
– классу![]() .
.
Относительно
точки
![]() говорят, что онапроизводит
сечение (дедекиндово
сечение)
отрезка,
ее называют дедекиндовой
точкой.
говорят, что онапроизводит
сечение (дедекиндово
сечение)
отрезка,
ее называют дедекиндовой
точкой.
Теорию, построенную на аксиомах I-IV группы, называют абсолютной геометрией. К ней, в частности, относятся теория измерения отрезков и углов, теоремы о пересечении прямой и окружности, двух окружностей. Особо выделим следующие теоремы абсолютной геометрии.
Т е о р е м а. (Первая теорема Саккери-Лежандра). Сумма углов треугольника меньше или равна двум прямым углам.
Т е о р е м а. Через точку вне прямой можно провести прямую, не пресекающуюся с данной прямой.
V. Аксиома параллельных.
5.1. (Предложение Плейфера). Через точку вне прямой можно провести не более одной прямой, не пересекающейся с данной.
Две прямые плоскости, не имеющие общей точки, называются параллельными прямыми.
Из аксиомы параллельных и теоремы 12 следует, что через точку вне прямой проходит единственная прямая, параллельная данной.
Опираясь на аксиомы I-V группы можно установить существование подобных фигур, доказать теорему Пифагора, развить теорию измерения площадей и многое другое, что составляет содержание евклидовой геометрии плоскости.
С современной точки зрения аксиоматика Гильберта представляется чрезвычайно сложной и неоправданно громоздкой. Надо обладать большим терпением, чтобы с помощью этой аксиоматики добраться до узловых теорем геометрии и при этом не запутаться в огромном количестве промежуточных
лемм, теорем и следствий.
В теории
этой аксиоматики достаточно сложно
вводятся понятия расстояния между
точками, длины отрезка, величины
угла.
Недостатком является и то
обстоятельство, что она никак не связана
с понятием векторного пространства,
которое в наше время играет в математике
важную роль. Немецкий математик Герман
Вейль в 1918 году предложил аксиоматику
евклидова пространства, основанную на
широком применении понятия вектора.
Можно доказать, что аксиоматики
![]() Гильберта и
Гильберта и![]() Вейля эквивалентны, то есть, теории,
определяемые ими, совпадают.
Вейля эквивалентны, то есть, теории,
определяемые ими, совпадают.
