Лекция 3. Понятие поверхности. Гладкие поверхности. Координатная сеть на поверхности. Касательная плоскость и нормаль к поверхности §8. Векторная функция двух скалярных аргументов

Пусть – трехмерное векторное пространство над полем вещественных чисел,– некоторое подмножество пространтсва.

Если задано отображение в, то имеемвекторную функцию двух скалярных аргументов.

В наших рассуждениях мы, как правило, будем рассматривать векторные функции, определенные на множестве , являющемсядвумерной областью. Это означает, что является связным (любые две его точки можно соединить элементарной кривой, содержащейся в) и каждая точкаимеет окрестность, содержащуюся вили пересекающуюся с ним по полукругу с границей. Примерами двумерных областей могут служить всё пространтсво, замкнутое числовое пространство, состоящее из всех точек, для которых, числовой квадрат, состоящий из всех точек, для которых.

Задание в векторном пространстве базиса приводит к трем числовым функциям двух аргументов

.

Для векторных функций двух аргументов, по аналогии с векторными функциями одного аргумента, определяются понятие предела, непрерывности.

Если фиксировать одну переменную, то будем иметь функцию одной переменной, для которой можно искать производную. Если эта производная существует, то она называется частной производной векторной функции:

.

Частные производные существуют тогда и только тогда, когда существуют частные производные координат векторной функции, при этом

.

Если векторные функции дифференцируемы в точке, то вектор

называется дифференциалом векторной функции в точке , при этом. Векторная функция в этом случае называетсядифференцируемой в точке .

Векторная функция называется дифференцируемой, если она дифференцируема в каждой точке своей области определения.

§9. Понятие поверхности

Откладывая значения векторной функции от начала прямоугольной системы координат, получим множество концов векторов, которое называетсягодографом векторной функции.

Элементарной поверхностью называется множество точек пространства, являющее годографом взаимно однозначной непрерывной векторной функции, определенной в двумерной области.

Имеем векторное уравнение поверхности

,

параметрические уравнения поверхности

.

Примерами элементарных поверхностей являются параболический цилиндр, эллиптический параболоид, гиперболический параболоид, полусфера с границей и без границ.

Для того, чтобы изучать поверхность средствами дифференциального исчисления, необходимо, чтобы она задавалась векторной функцией, имеющей непрерывные частные производные.

Гладкой поверхностью класса , называется годограф векторной функции, определенной в двумерной области и имеющей непрерывные частные производные по любым наборам переменных до порядкавключительно, при условии, что в каждой его точке векторынеколлинеарны.

Имеет место

Т е о р е м а. Вблизи каждой своей точки гладкая поверхность представляет собой элементарную поверхность.

Вблизи каждой точки гладкой поверхности мы имеем взаимно однозначное соответствие между точками поверхности и парами чисел из соответствующей области определения. На этом основании параметрыназываютсякриволинейными координатами на поверхности.

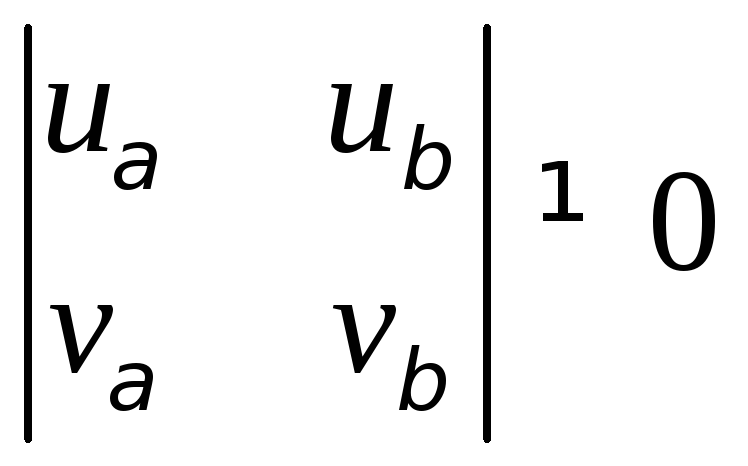Взаимно однозначные и взаимно непрерывные функции , имеющие непрерывные частные производные до порядкавключительно, такие, что, приводят к новой параметризации поверхности