Лекция 4. Система аксиом Гильберта евклидовой геометрии §7. Обзор аксиоматики Гильберта евклидовой геометрии

В 1899 году вышла знаменитая книга немецкого математика Д. Гильберта «Основания геометрии». В этой книге впервые дан список аксиом, достаточный для логического построения евклидовой геометрии. Тем самым было доказано, что геометрия – формально дедуктивная система, все предложения которой выводятся чисто логически из некоторого числа основных допущений – аксиом.

База в аксиоматике Гильберта евклидовой плоскости – это символы E и F, обозначающие множества, элементы которых будем называть соответственно точками и прямыми.

Символы обозначаютотношения на множествах базы:

– –отношение «принадлежности». Если , то будем говорить, что точка лежит на прямой , илипроходит через точку, и обозначать.

– –отношение «лежать между». Если , то будем говорить, что точка лежит между точками ии обозначать.

– –отношение «конгруэнтности».

О п р е д е л е н и е. Любая совокупность точек называется фигурой. Множество всех фигур P(E) – множество всех подмножеств множества E. Если , то будем говорить, что фигураконгруэнтна фигуре, и обозначать.

Отметим, что прямую не следует представлять как специальное множество точек. Ее нужно мыслить как самостоятельный единый объект, не разлагающийся на точки.

Точки, прямые, отношения «принадлежности», «лежать между» и «конгруэнтности» – это любые два сорта элементов и любые три отношения, которые удовлетворяют системе аксиом, содержащей 15 утверждений, разбитых на 5 групп:

I группа – аксиомы принадлежности; II группа – аксиомы порядка; III группа – аксиомы конгруэнтности; IV группа – аксиомы непрерывности; V группа – аксиома параллельных.

I. Аксиомы принадлежности.

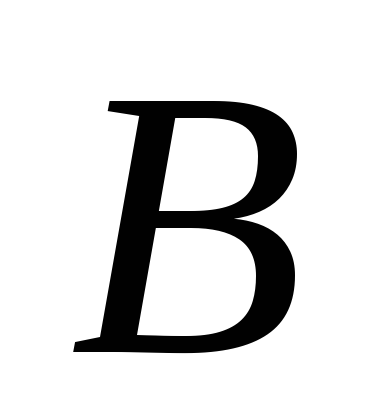1. Через любые две различные точки ипроходит единственная прямая(будем обозначать).

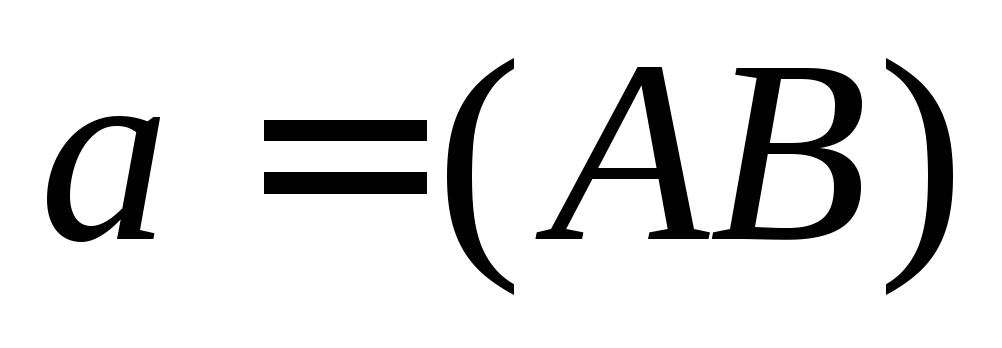2. На всякой прямой лежат, по крайней мере, две точки.

3. Существуют, по крайней мере, три точки, не лежащие на одной прямой.

Исходя из этих аксиом можно доказать ряд теорем, которые в школьном курсе геометрии не доказываются, так как наглядно очевидны. Например

Т е о р е м а. Если точка не лежит на прямой, проходящей через точкии, то не существует прямой, на которой лежат все три точки.

Т е о р е м а. Если две различные прямые ипроходят через точку, то

1) каждая точка , лежащая на одной из прямых и отличная от, не лежит на другой прямой;

2) если точка лежит на прямой, точкалежит на прямойи точкиине совпадают с, то не существует прямой, проходящей через три точки.

Т е о р е м а. Две различные прямые могут иметь не более одной точки, лежащей одновременно на обеих прямых.

II. Аксиомы порядка.

1. Если точка лежит между точкамии, то– различные точки, лежащие на одной прямой, и точка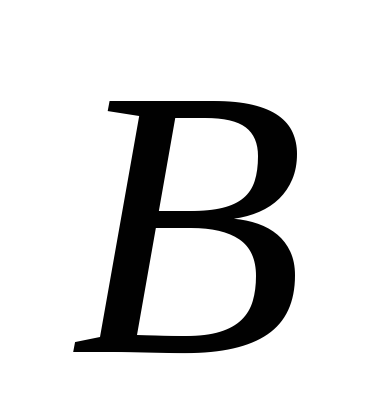лежит междуи.

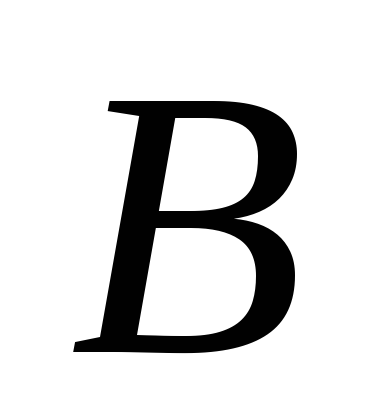2. Для любых двух различных точек исуществует, по крайней мере, одна точка, что.

3. Среди любых трех точек, лежащих на одной прямой, существует не более одной точки, лежащей между двумя другими.

Далее можно определить, по Гильберту, отрезок, треугольник.

О п р е д е л е н и е. Отрезок – это пара точеки. Обозначение:. Точкии–концы отрезка; любая точка, лежащая между иназываетсявнутренней точкой отрезка или просто точкой отрезка.

О п р е д е л е н и е. Треугольником называются три точки, не лежащие на одной прямой. Точки, определяющие треугольник, называются вершинами треугольника, а отрезки, определяемые вершинами треугольника – сторонами треугольника.

4. (Аксиома Паша). Пусть точки 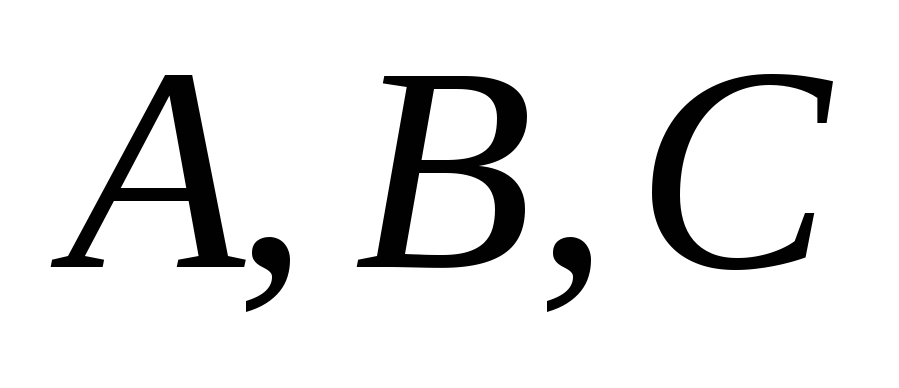не лежат на одной прямой и прямаяне проходит ни через одну из них. Еслипроходит через внутреннюю точку отрезка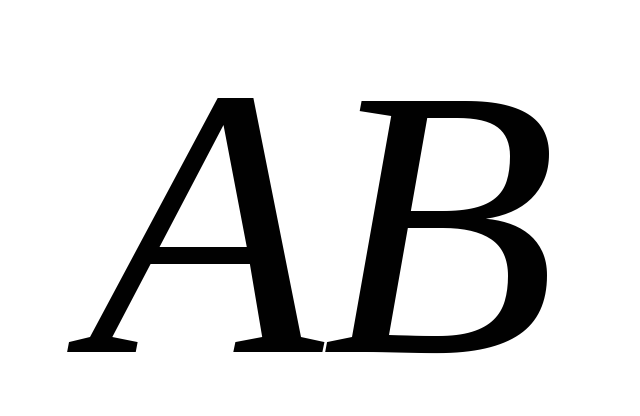, то она проходит и через внутреннюю точку одного из отрезковили.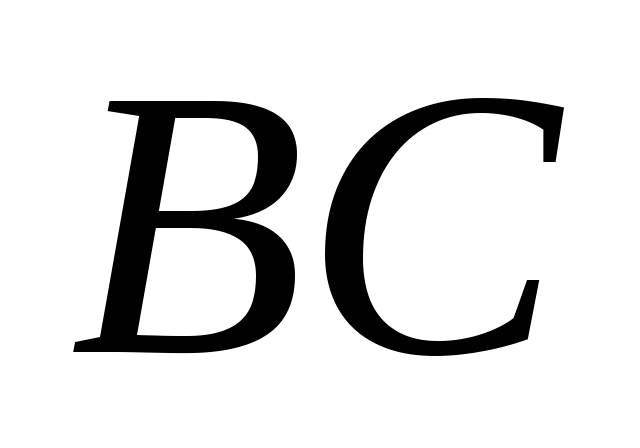

С помощью аксиом I, II групп можно доказать многие факты и ввести ряд основных определений. Среди них определение луча, угла, полуплоскости.