§6. Канонический репер

Пусть – гладкая кривая класса. Всякая прямая, проходящая через точкугладкой кривой перпендикулярно касательной в этой точке, называетсянормалью этой кривой в точке . Все нормали кривой в точкерасположены в одной плоскости, которая называетсянормальной плоскостью кривой в точке .

Вторая производная 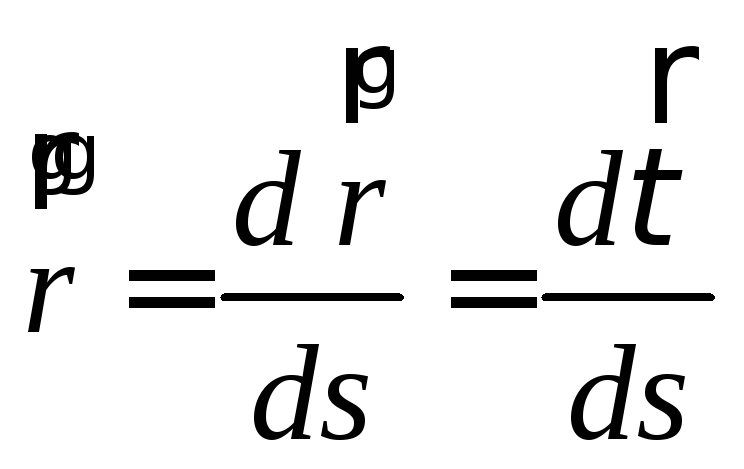вектор-функциинатурального параметра, задающей кривую, ортогональна единичному вектору касательной как производная вектора постоянной длины. Таким образом, если векторненулевой в точке, то он направлен по некоторой нормали кривой в этой точке. Эта нормаль называетсяглавной нормалью кривой. При этом орт вектора называетсяединичным вектором главной нормали и обзначается .

Если в точке , то главная нормаль не определена, при этом точканазываетсяточкой распрямления.

Длина вектора называетсякривизной кривой в данной точке: . Таким образом,.

Пусть точка кривой не является точкой распрямления. Тогда плоскость, проходящая через касательную и главную нормаль кривой в точке, называетсясоприкасающейся плоскостью кривой в данной точке. Из соотношений

,

Следует, что при любой параметризации гладкой кривой класса векторы, вычисленные в точке, не являющейся точкой распрямления, всегда лежат в соприкасающейся плоскости кривой в этой точке.

Нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Её направляющий вектор называетсяединичным вектором бинормали.

Касательная, главная нормаль и бинормаль определяют в каждой точке, не являющейся точкой распрямления гладкой кривой, трехгранник с тремя прямыми углами при вершине, совпадающей с точкой кривой. Этот трехгранник называется сопровождающим, основным или натуральным трехгранником.

Гранями основного трехгранника будут три взаимно перпендикулярные плоскости: соприкасающаяся плоскость , нормальная плоскость, спрямляющая плоскость.

Ортонормированный репер называютканоническим репером линии в точке .

§7. Формулы Серре-Френе

Для гладкой кривой класса без точек распрямления изменение векторовпри движении точки по кривой описывается формулами Серре-Френе, дающими разложение производных по натуральному параметру векторовпо этим же векторам.

Имеем

. (1)

Так как – векторная функция постоянной длины, то, и, следовательно,параллелен спрямляющей плоскости. Поэтому его можно разложить по векторами:

(2)

Дифференцируя тождество по параметруи учитывая формулы (1), (2), получим. Таким образом,

(3)

Дифференцируя тождество , получим.

Число называетсякручением линии в точке.

Таким образом, формулы Серре-Френе имеют вид:

Используя формулы Серре-Френе, можно доказать теоремы, раскрывающие геометрический смысл обращения внуль кривизны и кручения.

Т е о р е м а 1. Кривизна гладкой линии класса , равна нулю в каждой её точке тогда и только тогда, когда линия является промежутком прямой.

Т е о р е м а 2. Кручение гладкой линии класса , равно нулю в каждой её точке тогда и только тогда, когда линия является плоской.

Используя правила дифференцирования сложной функции и формулы Серре-Френе, получаем для гладкой кривой класса :

;

;

.

Тогда ,;.

Получаем формулы для вычисления кривизны и кручения кривой, заданной в произвольной параметризации:

, .

Для гладкой кривой класса , без точек распрямления имеем функции , которые называютсянатуральными уравнениями кривой, поскольку имеет место следующая

Т е о р е м а. Пусть и– две непрерывные числовые функции, причем. Тогда существует единственная с точностью до движения в пространстве гладкая кривая, для которойислужат кривизной и кручением.