3.4.5. Спектр комплексной экспоненты

Рассмотрим комплексный сигнал вида s(t) Ee j 0t. Спектр такого сигнала равен

S( j )	Ee j 0te j tdt E e j( 0)tdt 2 E ( 0).

Спектр комплексного сигнала представляет собой одиночную взвешенную-функцию (рис. 3.8,б). Сигнал не является вещественным, поэтому амплитудный спектр теряет свойство четности.

а	б

Рис. 3.8. Амплитудные спектры постоянного во времени сигнала (а) и комплексной экспоненты (б)

Заметим, что модель комплексного сигнала является удобным средством анализа модулированных сигналов, особенно при сложных видах модуляции, предусматривающих одновременное изменение амплитуды и фазы. Такая модель сигнала анализируется в следующем разделе 4.

3.4.6. Спектр гармонического сигнала

Определим спектральную плотность гармонического сигнала

s(t)

E cos( 0t ).

E

S( j )

Ecos( 0t )e j tdt

e j( 0t )

e j( 0t ) e j tdt

2

E

j

j(

)t

E

j

j(

)t

e

e

0

dt

e

e

0

dt.

2

2

Окончательно

S( j ) A e j ( 0) A e j ( 0 ).

Спектральная плотность гармонического сигнала представляет собой пару взвешенных -функций, расположенных на частотах 0. Веса -функций отражают комплексную амплитуду гармонического сигнала.

3.4.7. Спектральная плотность прямоугольного видеоимпульса

Спектральную плотность прямоугольного видеоимпульса (рис. 3.9) определим двумя способами:

1)непосредственным вычислением прямого преобразования Фурье;

2)использованием свойств преобразования Фурье.

Первый способ.

Вычисляем прямое преобразование Фурье, учитывая ограниченную длительность сигнала и постоянство амплитуды в пределах длительности:

и 2

и

2

e

j

и

2

e

j

и

2

S( j )

Ee j tdt

E

e j t

E

,

j

j

и

2

и

2

S( ) E и sin и 2 .

и 2

Рассматривался четный сигнал, поэтому его спектральная плотность содержит только действительную часть (см. рис. 3.9,б).

Амплитудный спектр представляет собой функцию типа sin x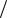x. Он имеет лепестковый характер, причем ширина лепестков равна 2 и , т.е. обратно пропорциональна длительности импульса. Нули спектра определяются из урав-

нения sin ( и	2) 0:				2
	и 2 k ,	k 1, 2, 3, ,	k	k		.
				и
Значение спектральной плотности импульса при 0 равно произведе-
нию E и , т.е.	S(0) равно площади импульса.

При увеличении длительности импульса ширина лепестков спектра уменьшается, при этом увеличивается значение S(0). При уменьшении длительности импульса ширина лепестков увеличивается, значение S(0) уменьша-

ется. При и	0	точки спектра k	k	2	удаляются в бесконечность и бес-
			и

конечно малая спектральная плотность становится равномерной в бесконечной полосе частот. При и точки спектра k приближаются к нулю и бесконечно большая спектральная плотность приобретает вид -функции (с полосой частот, равной нулю).

Фазовый спектр (см. рис. 3.9,б) принимает лишь два значения: 0 и в зависимости от знака функции sin xx. Значения фазы и неразличимы, разные знаки для фазового спектра при 0 и 0 использованы лишь с целью представления его в виде нечетной функции.

аб

Рис. 3.9. Прямоугольный импульс и его производная (а), спектр прямоугольного импульса (б)

При сдвиге импульса по оси времени на величину t t0 спектральная плотность в соответствии со свойствами преобразования Фурье приобретает вид

sin и

2

j t

sin и

2

j t

S( ) E и

e

E и

e

0 .

и

2

и 2

Как видно из этого выражения, амплитудный спектр не изменяется, а фазовый спектр свидетельствует о линейной зависимости фазы от частоты со скачками на в точках k (штриховая линия на рис. 3.9,б).

Второй способ.

Определяем сигнал s1(t), равный производной от рассматриваемого пря-

моугольного видеоимпульса, т.е. s1(t) ds(t). Этот сигнал представляет собой dt

две взвешенные -функции (см. рис.3.9,а). Спектральная плотность сигнала s1(t) будет равна сумме спектральных плотностей -функций, а именно:

S1( j ) E

	и		j t				и		j t
t		e		dt E		t		e		dt
	2						2

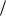E e j и 2 e j и 2 .

Спектральная плотность прямоугольного импульса, являющегося интегралом от сигнала s1(t), получается делением спектра S1( j ) на j (см. свойства преобразования Фурье):

	S ( j )		E e j и	2 e j и	2			sin(	и	2)
S( j )	1						E и				.
	j			j				и	2

Второй способ вычисления спектральной плотности является более простым.

3.4.8. Спектральная плотность произвольного периодического сигнала

Периодический сигнал может быть представлен рядом Фурье в комплексной форме

s(t)	Cke jk 1t ,
	k

где 1 2 – частота первой гармоники, равная частоте сигнала.

T

Учитывая результаты, полученные при вычислении спектра комплексного сигнала, можно сделать вывод, что спектральная плотность произвольного периодического сигнала представляет собой набор -функций, расположенных на частотах гармоник ряда Фурье. Веса -функций равны соответствующим коэффициентам ряда Фурье, умноженным на 2 .

3.4.9. Спектральная плотность сигнала вида sin xx

При рассмотрении вопросов дискретизации непрерывных сигналов возникает необходимость знать спектр сигнала, описываемого функцией sin xx . Вычисление спектра будем производить по формуле прямого преобразования Фурье. Итак, пусть задан сигнал

s(t) Asin mt ,

mt

где m 2 fm 2 , T – период функции sin mt .

T

Нули сигнала определяются так:

mt k при k 1,					2, ;	t	k	.
Тогда						m
sin mt			j t		sin mtcos t
S( j ) A		e		dt 2A					dt
mt					0	mt

A

sin( m)t

A sin( m)t

dt

dt.

m 0

t

m 0

t

Из таблицы определенных интегралов [10]:

при

a 0 ,

sinax

0

2

dx

x

a 0.

при

2

Тогда при

m S( j ) 0, а при

m

S( j ) A m . Таким об-

разом, спектральная плотность сигнала типа sin xx вещественная (сигнал четный), амплитудный спектр имеет форму прямоугольного импульса. Конкретно

для рассматриваемого сигнала s(t) Asin mt амплитудный спектр ограничен

mt

полосой частот 2 m , в пределах которой уровень спектра равномерен и равен

(рис. 3.10)

A A A .

m 2 fm 2fm

Рис. 3.10. Сигнал s(t) Asin mt и его спектр

mt

Аналогичный результат может быть получен из свойства дуальности преобразования Фурье. В соответствии с этим свойством, если четному сигналу s(t) соответствует спектральная плотность S( j ), то сигналу S(t) будет соответствовать спектральная плотность 2 s( j ).

Известно, что прямоугольному импульсу длительностью и и амплитудой

E соответствует спектральная плотность E и sin( и 2). Это значит, что сиг-

( и 2)

налу типа sin xx соответствует амплитудный спектр, имеющий прямоугольную