Емелянов Фундаменталные симметрии 2008

Qi

→U ij

Q j

;

ui

→U ij

u j

;

di

→U ij

d j

;

L

QL

L

R

uR

R

R

dR

R

(3.42)

Li

→U ij

Lj

;

ei

→U ij e j

L

LL

L

R

eR

R

Это симметрия случайная в том смысле, что она изначально не предполагается, но следует из фермионного содержания и калибровочных симметрий стандартной модели. Глобальная [U(3)]5- симметрия нарушается юкавской связью фермионов с хиггсовским полем:

L	= −ΓijQ	i	εφ*u j	−ΓijQ	i	φd j	−Γij	Li	φe j	+ э.с.,	(3.43)
Юкава	u L		R	d L		R	e L		R

где Γu , Γd , Γe – 3×3 комплексные матрицы в пространстве поко-

лений. Только малая подгруппа [U(3)]5 не нарушена, она соответствует барионному числу:

Qi	→ eiθ/3Qi	;	ui	→ eiθ/3ui	;	d i	→ eiθ/3d i	,	(3.44)
L	L		R	R		R	R

а также лептонному числу

LiL → eiφLiL ; eRi → eiφeRi .

(3.45)

Таким образом, барионные и лептонные квантовые числа можно рассматривать как проявление случайных глобальных симметрий стандартной модели. Когда хиггсовское поле φ приобретает вакуумное среднее

	0
< φ >=	υ		,	(3.46)
	2

фермионы (за исключением нейтрино) становятся массивными за счёт юкавских связей с хиггсовским полем в лагранжиане (3.43):

L

Юкава

= −M ij

u

i u j − M ij d

i d j

− M ije i e j

+ э.с.

(3.47)

u

L R

d

L

R

e L R

где

M

ij

= Γ

ij

υ

–

(3.48)

2

фермионная массовая матрица.

= γ0 (ΨC )*

Таким образом,

поля ΨL

и

ΨR

объединяются и

L

придают массы ui ,

d i ,

ei . Нейтринное поле νL

не несёт ненару-

121

шенной калибровочной симметрии, поэтому оно могло бы, в принципе, приобрести майорановскую массу

	−	1	M νij (νiTL CνiL + э.с.) ,	(3.49)
		2

однако это слагаемое в лагранжиане подавлено случайной симметрией лептонного квантового числа. На самом деле, барионные и лептонные числа оказываются аномальными, а их разность – нет. Обычно говорят, что майорановская масса нейтрино подавлена (B-L) симметрией.

Юкавские матрицы Г в лагранжиане (3.43) представляют собой 3×3 комплексные матрицы. Поскольку их три, то это вносит в теорию 3×3×3×2=54 новых параметра. Однако, как будет видно, только некоторые из этих параметров физически значимы.

Для лагранжиана (3.47) можно проводить вычисления физических процессов. Однако удобнее произвести переопределение полей, чтобы наиболее отчётливо проявилось физическое содержание теории. Эти переопределения не изменяют предсказаний теории, они аналогичны замене переменных при интегрировании.

Чтобы получить массы фермионов, проведём унитарное преобразование полей и диагонализируем массовые матрицы в лагран-

жиане (3.47):

ui

= Aij

u ' j

;

ui

= Aij

u ' j

; d i

= Aij

d ' j

;

d i

= Aij

d ' j

;

L

uL

L

R

uR

R

L

dL

L

R

dR

R

(3.50)

ei

= Aij

e' j

;

ei

= Aij e' j

;

νi

= Aij

ν' j .

L

eL

L

R

eR

R

L

νL

L

Каждая матрица A должна быть унитарной, чтобы сохранить форму слагаемого кинетической энергии в лагранжиане (3.41):

L

= iu

L

∂u

L

= iu '

L

A+

∂A

∂u '

L

= iu '

L

∂u '

L

.

(3.51)

кинет

uL

uL

При диагонализации массовых матриц возникают массы фермионов. Эти преобразования диагонализуют также юкавские матрицы Г, поскольку они пропорциональны массовым матрицам (3.48).

Нужно, однако, рассмотреть, как переопределение полей влияет на оставшуюся часть лагранжиана. Переопределение не влияет на калибровочную или хиггсовскую часть лагранжиана, так как они не

122

зависят от фермионных полей. Однако это переопределение могло бы влиять на Lматерия . Но набор переопределённых полей имеет глобальную [U(3)]5-симметрию, поэтому не изменяет Lматерия . Определим, сколько физически значимых параметров остаётся после переопределения полей. Начнём с кваркового сектора. Число параметров, содержавшихся в комплексных матрицах Γu , Γd :

2×3×3×2=36. Унитарные симметрии UQL , UuR , UdR входят в пе-

реопределение кварковых полей. Как уже говорилось, они не оказывают влияния на Lматерия . Эти симметрии дают 3×3×3 степеней

свободы (унитарные N×N матрицы содержат N свободных параметров). Таким образом, полное число степеней свободы, остающихся в полном лагранжиане после переопределения полей:

2 3 3 2 – (3 ×3 ×3 – 1) = 10,

(3.52)

где вычтено барионное квантовое число. Барионное число связано с симметрией юкавской части лагранжиана (3.43), поэтому его нельзя использовать для диагонализации массовых матриц. Десять оставшихся параметров соответствуют шести кварковым массам и четырём параметрам матрицы Кабиббо-Кабаяши-Маскава (три угла смешивания и одна CP-нарушающая фаза).

До сих пор мы считали нейтрино безмассовыми. Однако нейтрино имеют массу. Почему бы не расширить стандартную модель, включить поле NR и добавить юкавское взаимодействие:

LЮкава = −Γijγ

LiLεφ*NRj + э.с.

(3.53)

Покажем, что поле NR стерильно, т.е. не несёт калибровочных квантовых чисел, но несёт лептонное квантовое число +1. Действительно, поля LL и φ имеют равные, но противоположные по знаку гиперзаряды, т.е. NR должно иметь нулевой гиперзаряд, чтобы

LЮкава был калибровочно-инвариантным. Поскольку LL и εφ* преобразуются как SU(2)L-дублеты, то LЮкава будет калибровочноинвариантным, если NR -синглет по отношению к SU(2)L. Чтобы

LЮкава сохранял лептонное число, мы должны приписать полю NR

123

лептонное число +1. Тогда, если хиггсовское поле приобретает вакуумное среднее, то нейтрино, подобно другим фермионам, получает дираковскую массу.

К сожалению, при таком подходе возникают следующие трудности:

а) почему нейтрино гораздо легче других фермионов?

б) поскольку NR стерильно, калибровочные симметрии допускают майорановский массовый член

	L = −	1	M Rij NRiT CNRj	+ э.с.	(3.54)
		2

С таким массовым слагаемым поля νL и NR при формировании

дираковского фермиона не объединяются. При этом возникает два майорановских нейтрино на каждое поколение. Это больше, чем необходимо для описания природы.

Очевидно, что майорановский массовый член (3.54) подавлен, если симметрия, связанная с лептонным числом, – точная симметрия. В этом случае нейтрино могло бы приобрести дираковскую массу за счёт юкавского взаимодействия. Напомним, что симметрия, связанная с лептонным числом – случайная симметрия стандартной модели, и нет причин ожидать, что она является точной симметрией расширенной стандартной модели. Даже если бы этот сценарий был реализован в природе, то мы должны рассматривать его как проявление физики вне стандартной модели, поскольку он требует введения двух новых предположений: поля NR и проявле-

ния лептонного числа как следствия не случайной, а точной симметрии.

Прежде чем вводить поле NR , рассмотрим стандартную модель

как низкоэнергетическую эффективную полевую теорию с лагранжианом, который является разложением по обратным степеням некоторой массы M:

	L = L	+	1	dim(5) +	1	dim(6) +...	(3.55)
			M		M 2
	СМ

Слагаемые вне стандартной модели представляют собой операторы возрастающей размерности, начиная с размерности пять. Для

124

набора полей на калибровочных симметрий стандартной модели существует только один оператор размерности пять:

L	=	Cij	LiT εφCφT εLj		+ э.с.	(3.56)
5		M	L	L

где Cij – симметричная комплексная матрица.

Покажем, что лагранжиан L5 SU(2)L×U(1)Y –инвариантен и нарушает лептонное число. Очевидно, что комбинация LTLεφ –

SU(2)L×U(1)Y-инвариантна, поэтому L5 – калибровочно-инвариан- тен. Лептонное число нарушается, так как поле LL несёт заряд

L = + 1, а L5 имеет L = + 2.

Когда хиггсовское поле приобретает вакуумное среднее (3.46),

нейтрино получает майорановскую массу
L	= −	Cij		υ2	νiT Cν j	+ э.с.	(3.57)
				M
майор	2				L L

Отметим, что нейтрино получает майорановскую массу, поскольку лептонное число нарушается слагаемым L5 в полном лагранжиане. Таким образом, лептонное число отражает лишь низкоэнергетическую случайную симметрию и, вообще говоря, нарушается операторами высших размерностей.

Из соотношения (3.57) следует, что масса нейтрино ~υ2/M. Поэтому при M~υ масса нейтрино гораздо меньше υ. Это очень привлекательное объяснение, почему нейтрино гораздо легче других фермионов.

Вернёмся к обсуждению стерильного нейтрино NRi и покажем,

что соотношение (3.57) возникает в предположении о том, что стерильное нейтрино очень тяжёлое.

Начнём с лагранжианов (3.53), (3.54):

	L = −		LΓνεφ*NR −	1	NRT M RCNR + э.с.,	(3.58)
		L
				2
	где для простоты опущены некоторые индексы. Если MR					– очень

большая, то поле NR отсутствует при низких энергиях, и по нему можно проинтегрировать. При низких энергиях NR – нединамиче-

125

ское классическое поле, и его можно исключить, решив уравнение движения

∂L	= 0	(3.59)
∂NR

и подставив его значение в лагранжиан (3.58). Тогда из (3.58) имеем

	C	= −	1	(ΓνM R−1ΓTν )+ .	(3.60)
	M		2

Отсюда видно, что масса M в эффективной теории (3.55) пропорциональна массе MR . При этом нарушается описание в рамках эф-

фективной полевой теории, если энергии сравнимы с массой тяжёлого майорановского нейтрино.

Покажем, что соотношение (3.60) действительно выполняется. Для этого найдём

∂L

= −

LΓνεφ* − NRT M RC + э.с.

(3.61)

L

∂NR

Решая уравнение

∂L

= 0 относительно N , получаем

∂NR

R

NR = φ+εCγ0 (ΓνM R−1)L*L .

(3.62)

Подставим NR в лагранжиан

1

+

*

−1

T

+ *

L =

LLεφ CΓ

ν(ΓνM R

)

φ εL

+ э.с.

(3.63)

2

Это выражение есть ни что иное, как лагранжиан (3.56), если идентифицировать первый член в (3.63) с эрмитово сопряжённым слагаемым в L5 . Отсюда получаем

	C +	= −	1	Γν(ΓνM R−1)T	(3.64)
	M		2

которое совпадает с выражением (3.60), если вспомнить, что C – симметричная матрица.

На рис. 3.1 изображён спектр масс нейтрино одного поколения для двух обсужденных нами предельных случаев.

126

Рис. 3.1

Если M R ~ υ, то NR – тяжёлое майорановское нейтрино массы MR и νL – очень лёгкое майорановское нейтрино массы 0(υ2/ MR ) . В другом предельном случае MR = 0 (если лептонное число является проявлением точной симметрии) поля νL и NR объединяются

и дают дираковскую массу нейтрино ~0(υ).

Поэтому дираковское нейтрино можно рассматривать как состояние двух вырожденных майорановских нейтрино. Если тяжёлое нейтрино массы MR придаёт лёгкому нейтрино массу

0(υ2/ MR ) , то говорят о see-saw механизме формирования массы нейтрино.

3.3.3. Симметрии хиггсовского сектора

Обратимся теперь к хиггсовскому сектору нарушения электрослабой симметрии. Обсудим глобальные симметрии этого сектора.

Хиггсовский сектор стандартной модели описывается лагранжианом

L

= (D φ)+ (Dμφ) −V (φ) ,

(3.65)

Хиггс

μ

где хиггсовский потенциал

V (φ) = −μ2φ+φ+ λ(φ+φ)2

(3.66)

и ковариантная производная

D

φ =

∂

μ

+ i

g

σW

+ i

g '

B

φ

(3.67)

μ

2

μ

2

μ

Хиггсовский сектор обладает SU(2)L×U(1)Y симметрией, а также приближённой (случайной) глобальной симметрией. Для того, что-

127

бы это увидеть, перепишем хиггсовский лагранжиан следующим образом. Обозначим компоненты хиггсовского дублета

	φ+		(3.68)
φ =	φ0

Тогда εφ* – тоже SU(2)L-дублет, имеющий компоненты

	φ0*		,	(3.69)
εφ* =
−φ−

где φ− = φ+*.

Определим хиггсовскую матрицу (или бидублет полей):

1

(εφ*,φ) =

1

φ0*

φ+

Φ =

−φ−

.

(3.70)

2

2

φ0

В терминах этой матрицы хиггсовский лагранжиан имеет вид

L

= tr(D Φ)+ Dμ

Φ −V (Φ) ,

(3.71)

Хиггс

μ

где потенциал

V (Φ) = −μ2trΦ+Φ + λ(trΦ+Φ)2 ,

(3.72)

а ковариантная производная

D

Φ =

∂

Φ + i

g

σW

Φ + i

g '

B

Φσ

.

(3.73)

μ

3

μ

2

μ

2

μ

Отметим появление матрицы Паули σ3. Она необходима, поскольку φ и εφ* имеют противоположный гиперзаряд.

Покажем, что выражения (3.65) и (3.71) идентичны. Для этого запишем матрицу как внешнее произведение двух векторов

	tr(Φ+Φ) =	1		−φT ε		(εφ*,φ) = φ+φ ,
			tr	φ+			(3.74)
		2

где использовано φT φ* = (φT φ* )T = φ+φ.

Таким образом, потенциалы действительно одинаковые. Для кинетического слагаемого имеем

D φ = (D (εφ* ), D φ) = (ε(D φ)*, D φ),					(3.75)
μ	μ	μ	μ	μ

где на последнем шаге использовано σε = −σεT = −σε*.

128

Преобразования группы симметрии SU(2)L×U(1)Y действуют на матрицу хиггсовских полей следующим образом:

SU(2)L: Φ→LΦ;			(3.76)
U(1)γ: Φ → Φe−	i	σ3θ
	2		,

где снова возникает матрица σ3 из-за противоположности гиперзарядов полей φ и εφ*.

Относительно преобразваний из SU(2)L:

tr(D Φ)+ D Φ → tr(D Φ)+ L+LDμΦ = tr(D Φ)+ DμΦ, (3.77)
μ	μ	μ	μ

т.е. это слагаемое инвариантно.

Чтобы обнаружить приближённую глобальную симметрию, рассмотрим предел, в котором константа связанная с гиперзарядом, g′→0. В этом случае лагранжиан сохраняет форму (3.71), однако ковариантная производная упрощается:

D	Φ =		∂		+ i	g	σW		Φ .	(3.78)
				μ
μ					2		μ

Видно, что в этом пределе лагранжиан обладает глобальной SU(2)R симметрией, т.е.

	SU(2)R: Φ→ΦR+.		(3.79)
Относительно преобразований из группы SU(2)R:
tr(D Φ)+ DμΦ → trR(D Φ)+ DμΦR+ = tr(D Φ)+ DμΦ,			(3.80)
μ	μ	μ

т.е. снова инвариантно.

Итак, в пределе g′→0 хиггсовский сектор стандартной модели

обладает глобальной симметрией SU(2)L×SU(2)R, при этом

Φ→LΦR+.

Когда хиггсовское поле приобретает ненулевое вакуумное среднее, матричное поле имеет вид

		1	υ		0
	< Φ >=			0	υ	.	(3.81)
		2

При этом нарушается как SU(2)L-симметрия, так и SU(2)R- симметрия:

L<Φ>≠<Φ>; <Φ>R+=<Φ>,

(3.82)

129

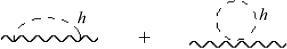
однако остаётся ненарушенной подгруппа SU(2)L+R, соответствующая взаимным SU(2)L и SU(2)R-преобразованиям с L=R, т.е.

L<Φ>L+=<Φ>. (3.83)

Таким образом, хиггсовское вакуумное среднее нарушает глобальную симметрию следующим образом:

SU(2)L×SU(2)R→SU(2)L+R . (3.84)

Иногда симметрию SU(2)L+R называют “custodial symmetry”. Поскольку SU(2) – трёхмерная группа, число нарушенных генераторов 3+3–3=3. В результате механизма Хиггса “уходит” три безмассовых голдстоуновских бозона, но возникают массы у W+, W– и Z-бозонов.

MW2 =

1

g 2υ2 ;

M Z2 =

1

(g 2

+ g'2 )υ2 .

(3.85)

4

4

При этом на древесном уровне

M 2

g 2

M 2

W

=

= cos2

θW или

ρ =

W

−1 , (3.86)

M Z2

g 2 + g

'2

M Z2 cos2

θW

θW – угол Вайнберга.

Таким образом, в пределе g′→0 W+, W– и Z-бозоны образуют триплет ненарушенной глобальной симметрии, поэтому при g′→0

MW = M Z .

Рассматриваемая нами симметрия хиггсовского сектора позволяет понять свойства теории вне рамок древесного приближения. Из-за ненарушенной SU(2)L+R симметрии в пределе g′→0 радиационные поправки к параметру ρ в соотношениях (3.86) должны быть пропорциональны g′2. Например, поправка к параметру ρ за счёт диаграмм с хиггсовскими петлями (рис. 3.2)

Рис. 3.2

130