Емелянов Фундаменталные симметрии 2008

перпартнеры известных частиц имеют гораздо большие массы, чем сами частицы.

Заметим, что механизм спонтанного нарушения симметрии находит свое применение в стандартной модели. Калибровочные бозоны и фермионы получают свои массы за счет ненулевого вакуумного среднего хиггсовского поля.

Обратимся теперь к систематическому рассмотрению простран- ственно-временных и внутренних симметрий. Начнём обсуждение с лоренцевской и конформной симметрий.

31

Глава 1 ЛОРЕНЦЕВСКАЯ И КОНФОРМНАЯ СИММЕТРИИ

1.1. Группа Лоренца

Это группа неоднородных преобразований Лоренца, т.е. группа преобразований, сопровождающихся пространственно-временны- ми трансляциями. Группа Пуанкаре является прямым произведением группы Лоренца и группы трансляций. Два оператора Казимира этой группы соответствуют квадрату массы и квадрату спина частицы. Действительно, масса частицы и ее спин – лоренцинвариантные величины.

Как построить представления группы Лоренца, имеющие физическое значение? Еще в 1939 г. Вигнер рассматривал подгруппы группы Лоренца, которые не изменяли 4-импульс свободной частицы. Максимальная подгруппа группы Лоренца, оставляющая 4-импульс, инвариантным была названа Вигнером малой группой. Поскольку малая группа не меняет 4-импульс частицы, то эта группа определяет внутренние пространственно-временные симметрии релятивистских частиц. Вигнер показал, что внутренние пространственно-временные симметрии массивных и безмассовых частиц определяются, соответственно, O (3) - и E (2) -подобными

малыми группами. O (3) -подобная малая группа локально изоморфна группе трехмерных вращений. Например, группа, описывающая спин электрона, является O (3) -подобной малой группой. Группа E (2) – евклидова группа двумерного пространства, вклю-

чающая трансляции и вращения плоского пространства. Группа лоренцевских преобразований состоит из трех сдвигов и трех вращений. Таким образом, вращения образуют подгруппу группы Лоренца. Если массивная частица находится в покое относительно некоторой системы отсчета, ее 4-импульс инвариантен относительно вращений. Поэтому малая группа массивной покоящейся частицы – группа трехмерных вращений. На что действует преобразование вращения? Очевидно, что вращение, вообще говоря, изменяет направление спина.

32

Если частица движется в z-направлении, она имеет ненулевую компоненту импульса в этом направлении. Сдвиг не изменяет алгебру Ли группы вращений, т. е. при этом «сдвинутая» малая группа будет сохранять 4-импульс. Если считать, что 4-импульс покоящейся частицы (0, 0, 0, m) , то трехмерная группа вращений остав-

ляет инвариантным 4-импульс, и ее генераторы

		0		0	0	0				0		0	i	0				0		−i 0		0
J			0	0	−i	0		, J			0	0	0	0		, J		i		0 0		0
	1	=	0	i	0	0			2	=	−i	0	0	0			3	=	0	0	0	0
			0	0	0	0					0	0	0	0					0	0	0	0

Генераторы удовлетворяют коммутационным соотношениям:

J	i	, J		= iε	ijk	J	k	.
			j

(1.1)

(1.2)

Для безмассовой частицы нельзя выбрать систему отсчета, в которой бы она покоилась. Вигнер показал, что малая группа безмассовой частицы, движущейся вдоль оси z, состоит из генератора вра-

щения вокруг оси z ( J3 в (1.1)) и двух других генераторов, имеющих вид

		0 0		−i	i					0		0 0		0
N		0 0		0	0		,	N			0	0	−i	i		(1.3)
	1	=	0 0		0				2	=	0	i	0	0	.
		i
			0 0		0						0	i	0	0
		i

Если обозначить через Ki генератор сдвига вдоль i-ой оси, то матрицы (1.3) можно представить в виде:

где		N1 = K1 − J2 ,						N2 = K2 + J1 ,								(1.4)
	0		0	0	i					0		0	0	0
		0	0	0	0		,	K			0	0	0	i		(1.5)
K =		0	0	0	0				2	=	0	0	0	0	.
1
			0	0	0						0	i	0	0
	i

Генераторы J3 , N1 и N2 удовлетворяют следующим коммутационным соотношениям:

33

[N , N	2	] = 0 ,	J	3	, N	1	= iN	2	,	J	3	, N		= −iN .	(1.6)
1													2	1

Ниже мы будем подробно обсуждать генераторы E (2) -группы. Здесь же отметим, что они включают J3 , связанный с вращением вокруг оси z, а также P1 и P2 , генерирующие трансляции вдоль осей x и y. Если заменить N1 и N2 в соотношении (1.6) на P1 и P2 , то это будут коммутационные соотношения для группы E (2) . По этой причине малой группой для безмассовых частиц является E (2) . Очевидно, что N1 и N2 генерируют лоренцевские преобра-

зования.

Нетрудно ассоциировать генератор вращений J3 со спирально-

стью безмассовой частицы. Какая физическая величина связана с N1 - или N2 -генераторами? Вигнер обнаружил существование этих

генераторов, но не дал физической интерпретации этим трансляционным генераторам. В течение многих лет рассматривались представления только с нулевыми собственными значениями операторов N. И только в 1971 г. Janner и Janssen связали преобразования, генерируемые этими операторами, с калибровочными преобразованиями.

1.1.1. Трансляции и калибровочные преобразования

Чтобы продемонстрировать идею Janner и Jansen, найдем мат-

рицу преобразования		exp (−i (uN1 + vN2 )) ,												(1.7)
генерируемую N1 и N2 . Это 4×4 матрица вида
1	0			−u					u
0	1			−v					v
	v			1			(u2 + v2 )				2			(1.8)
u													.
		−(u				)	2 1+ (u				)
			2	+ v	2			2	+ v	2		2
u 0
Если подействовать этой матрицей на 4-вектор
			p = (0, 0, ω, ω)											(1.9)
							34

безмассовой частицы, то 4-импульс остается неизменным. Таким образом, матрица (1.8) принадлежит малой группе. Если подействовать этой матрицей на электромагнитный 4-потенциал

A = ( A1, A2, A3, A0 )exp (i (kz − ωt )) ,

(1.10)

используя лоренцевское условие A3 = A0 , то в результате придем к

калибровочному преобразованию. Именно это обнаружили Janner и Janssen. N1 и N2 генерируют калибровочные преобразования.

1.1.2. Сжатие O(3) до E(2)

Покажем, как группа E(2) получается из группы трехмерных вращений в приближении плоской (цилиндрической) поверхности. При этой процедуре сжатия E(2)-симметрия безмассовых частиц возникает из O(3)-симметрии массивных частиц в пределе бесконечного импульса.

E(2)-преобразования включают вращение и две трансляции плоского пространства. Начнем с матрицы вращений, действующей на вектор-столбец ( x, y,1) :

cos θ		−sin θ	0
R (θ) = sin θ		cos θ	0	.
	0	0	1

Выберем матрицу трансляций в виде

1		0	a
T (a, b) =	0 1 b			.
	0	0	1
Произведение T (a, b) R (θ) :
		cos θ			−sin θ
E (a, b, θ) =T (a, b) R (θ) = sin θ					cos θ
			0		0

(1.11)

(1.12)

a

b . (1.13) 1

Это матрица евклидова преобразования в двумерной xy-плоскости. Матрицы R (θ) и T (a, b) относятся к подгруппам вращений и трансляций. Выражение (1.13) не является прямым произведением,

35

поскольку R (θ) и T (a, b) не коммутируют. Трансляции образуют

абелеву инвариантную подгруппу, поскольку различные матрицы T коммутируют друг с другом. Кроме того,

R (θ)T (a, b) R	−1	′ ′	(1.14)
		(θ) =T (a , b ) .

Подгруппа же вращений – неинвариантная, поскольку сопряжение

T (a, b) R (θ)T −1 (a, b)

(1.15)

не сводится к вращению.

Попытаемся записать трансформационную матрицу (1.13) в терминах генераторов. Вращения определяются генератором

	0	−i	0
J = i		0	0	.	(1.16)
3
	0	0	0

Трансляции связаны с генераторами

	0	0	i				0	0	0
P = 0		0	0		,	P = 0		0	i	.	(1.17)
1						2
	0	0	0				0	0	0

Эти генераторы удовлетворяют коммутационным соотношениям:

[P , P	] = 0 ,	J	3	, P		= iP ,	J	3	, P		= −iP .	(1.18)
1 2				1		2			2		1

Как получить E (2) малую группу из O (3) малой группы? Чтобы ответить на этот вопрос, запишем генераторы O (3) . Матрицы Ji задаются соотношениями (1.1). Евклидова группа E (2) определяется генераторами J3 , P1 , P2 , и их алгебра Ли обсуждалась выше.

Рассмотрим транспонированную алгебру Ли группы E (2) . Тогда P1 и P2 преобразуются в Q1 и Q2 :

	0	0	0				0		0	0
Q = 0		0	0		,	Q =		0	0	0	.	(1.19)
1		0	0			2		0	i	0
	i

Совместно с J3 эти генераторы удовлетворяют коммутационным

соотношениям:	] = 0 ,
[Q , Q		J	3	, Q		= iQ ,	J	3	, Q		= −iQ .	(1.20)
1 2				1		2			2		1
						36

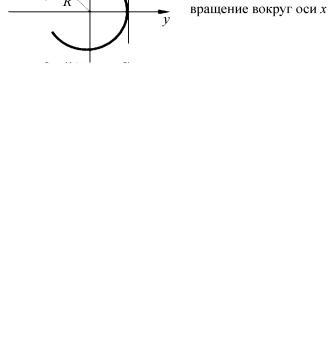
Эти матрицы генерируют преобразование точки на цилиндре. Вращения вокруг оси цилиндра генерируются J3 , матрицы же Q1 и

Q2 генерируют трансляции вдоль оси z цилиндра. Группа, вклю-

чающая эти матрицы, называется цилиндрической группой. Сжатия на евклидову и цилиндрическую группы можно достичь в пределе очень большого радиуса цилиндра:

	P =	1		B−1J				B ,		P = −		1			B−1J B ,	(1.21)
		R										R
	1					2				2					1
	Q = −			1	BJ	2	B−1		,	Q	=		1		BJ B−1 ,	(1.22)
	1			R						2			R		1
								1		0	0
где				B (R) =					0	1	0 .					(1.23)
									0	0	R
Векторные	пространства, на которые												действуют			генераторы, –
( x, y, z R)	и ( x, y, Rz)			соответственно для евклидовой и цилиндри-

ческой групп. Их можно рассматривать как приближение северного полюса и экваториальное приближение для сферической поверхности. На рис 1.1 показано, как происходит евклидово и цилиндрическое сжатие.

Рис. 1.1

37

Приближение «северного полюса» ведет к сжатию O (3) до

E (2) . Приближение «экваториальное» – к сжатию O (3)	до ци-
линдрической группы.
Поскольку P1 (P2 ) коммутируют с Q2 (Q1 ) , запишем следую-
щую комбинацию генераторов:
F1 = P1 +Q1 , F2 = P2 + Q2 .	(1.24)

Новые операторы удовлетворяют коммутационным соотношениям:

[F , F	] = 0 ,	J	3	, F		= iF ,	J	3	, F		= −iF .	(1.25)
1 2				1		2			2		1

Однако мы не можем, используя 3×3 матрицы Pi и Qi , построить 3×3 матрицы F1 и F2 , поскольку векторные пространства для Pi и Qi представлений различны. Однако это различие можно учесть,

добавив две различные z-координаты: одну для сжатых z, другую – для расширенных z: ( x, y, Rz, z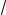R) .

Тогда генераторы имеют вид:

	0		0	0	i
P		0	0	0	0		,
	=	0	0	0	0
1
		0	0	0	0

		0		0	0	0
и	Q		0	0	0	0		,
		=		0	0	0
	1	i
			0	0	0	0

	0		0	0	0
P		0	0	0	i
	=	0	0	0	0
1
		0	0	0	0
	0		0	0	0
Q		0	0	0	0
	=	0	i	0	0	.
2
		0	0	0	0

(1.26)

(1.27)

Операторы F1 и F2 :

	0 0			0	i				0 0 0 0
F		0	0	0	0		,	F		0	0	0	i		(1.28)
	=		0	0	0				=	0	i	0	0	.
1	i							1
		0	0	0	0					0	0	0	0

Генератор вращения J3 выберем в виде (1.1). Тогда 4×4 матрицы

удовлетворяют E (2) -подобным коммутационным соотношениям (1.25). Матрицу B из (1.23) можно представить в виде:

38

1		0	0	0
	0	1	0	0
B (R) =	0	0	R	0	.	(1.29)
	0	0	0	1 R

Эта матрица включает как сжатую, так и расширенную координату светового конуса, показанные на рис. 1.2.

Рис. 1.2

Когда система испытывает Лоренц-сдвиг, одна из осей расширяется, а другая – сжимается. Как расширение, так и сжатие необходимы для сжатия O (3) -подобной малой группы до

E (2) -подобной малой группы.

Если произвести преобразование подобия матрицы (1.29), используя матрицу

1		0		0	0
	0	1		0	0			,	(1.30)
	0	0	1	2	−1	2
	0	0	1	2	1	2

что соответствует вращениям на 45° третьей и четвертой координат, то матрица (1.29) принимает вид:

39

1		0	0	0
	0	1	0	0		,	(1.31)
	0	0	cos η
				sin η
	0	0	sin η
				cos η

где R = eη. Это матрица лоренцевских сдвигов вдоль оси z. Если мы стартуем с набора расширенных генераторов вращений J3 в

соотношении (1.1) и приходим к соотношениям (1.21), то

N =

1

B−1J

B ,

N

= −

1

B−1J

B ,

(1.32)

1

R

2

2

R

2

причем N1 и N2

задаются соотношением (1.3). Генераторы N1 и

N2 – это сжатые генераторы

J2 и J1 , соответственно, в пределе

бесконечного импульса (или в безмассовом пределе).

Как отмечалось выше, N1 и N2 генерируют калибровочные

преобразования безмассовых частиц. Таким образом, сжатие поперечных вращений приводит к калибровочным преобразованиям.

Итак, мы показали, что для безмассовых частиц O (3) -подобная малая группа может быть сжата до E (2) -подобной малой группы. Был рассмотрен случай спина 1, но рассматриваемый механизм применим и для других спинов. Для частиц со спином 1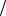2 сущест-

вуют калибровочные преобразования, и поляризация нейтрино является следствием калибровочной инвариантности.

1.2. Представления группы Лоренца

1.2.1. Преобразования Лоренца. Нормальные параметры

В релятивистской теории переход от одной инерциальной системы отсчета к другой, движущейся со скоростью v , задается лоренцевским преобразованием. Если скорость v параллельна оси OZ, эти преобразования выглядят следующим образом:

x → x; y → y; z →	1		(z + vt); t →
	1−	v2
		c2
			40

1			v
		t +		z	,	(1.33)
	v2		c2
1−
	c2