Емелянов Фундаменталные симметрии 2008

лика, то майорон будет, главным образом, связан с правыми нейтрино.

Рассмотрим более детально, как это происходит. В результате спонтанного нарушения как лептонного числа, так и SU(2)×U(1) симметрии, нейтринные поля приобретают как дираковский (фер- мион-антифермионный), так и майорановский массовый член

L

= −

1

(M

R

)

ij

[νT

ν

Rj

] − (M

D

)

ij

[ν

Li

ν

Rj

] + э.с.

(5.118)

масс

2

Ri

с дираковской массовой матрицей, пропорциональной дублетному хиггсовскому вакуумному среднему. Если собственные значения MR гораздо больше MD, тогда нейтринная массовая матрица

	0	M D	(5.119)
M =
M D		M R

содержит набор больших собственных значений, соответствующих собственным значениям MR , и набор чрезвычайно малых собствен-

ных значений, ассоциированных с матрицей M D2 / M R . В этом со-

стоит знаменитый “see-saw” механизм (Yanagida et.al.,1979). В ре-

зультате получается спектр нейтрино, содержащий как сверхтяжелые, так и чрезвычайно легкие состояния:

L

≈ −

1

M D2

η η

−

1

[M

] η

η

.

(5.120)

R

2i

2 j

масс

2

1i 1 j

2

ij

M R

ij

Легкие нейтрино η1i , главным образом, – левые, а тяжелые нейтрино η2i – правые. Хотя поле χ, в основном, связано с тяжелыми полями η2i , существует слабая связь χ с полями η1i . Таким обра-

зом, майорон, как результат смешивания масс нейтрино, имеет слабую связь с обычными левыми нейтрино

	взаим	hij	hM D2
	Lмайор = −		η2iiγ5η2 jχ −			η1iiγ5η2 jχ .	(5.121)
		2
			M R2				mν
	Майороновская связь с легкими нейтрино					~ M D2 / M R2 ~		, где
							M R

mν – масса легкого нейтрино. Майорон имеет еще более слабую

201

связь с обычной материей из-за смешивания χ с Z 0 на однопетлевом уровне

	Lэф	= i	m f			γ		f χ ,	(5.122)
					f		5
	материя		Vχ

где масштаб Vχ ≈ (GF mν )−1 >>ТэВ. Очевидно, что майорон в этой

модели легко удовлетворяет ограничению на диполь-дипольные взаимодействия в среде. Если майорон существует, то оказывается возможным распад наиболее тяжелого из легких нейтрино на другие нейтрино с испусканием майорона. Если процесс νi → ν j χ был

бы достаточно быстрым, то он мог бы открыть область нейтринных масс, подавленных космологией. Для стабильных нейтрино известно, что их массы в интервале от нескольких электронвольт до нескольких гига электронвольт исключены космологическими данными. Однако это рассмотрение не применимо для нестабильных нейтрино. Если время жизни по отношению к распаду νi → ν j χ

гораздо меньше времени жизни Вселенной T0 , то можно ожидать

красного смещения энергии νi за массу mνi							. Следовательно, вклад
таких нейтрино в плотность энергии Вселенной
ρ	νi	~ m		τ	1/2 T 3 ,		(5.123)
			νi T			ν
			0

где Tν – современная нейтринная температура Tν ~ Tγ ~ 3 K .

5.8. Глобальные симметрии и гравитация

Выше обсуждались различные глобальные симметрии взаимодействий в стандартной модели, однако необходимо рассмотреть роль гравитационных взаимодействий. По-видимому, наиболее простой способ убедиться в том, что гравитационные взаимодействия способны привести к серьезным проблемам – это обратиться к “no-hair” теореме для черных дыр. Эта теорема (Banks, 1990) утверждает, что черные дыры могут характеризоваться только несколькими фундаментальными величинами (массой, спином), но не

202

обладают другими квантовыми числами. Поскольку черные дыры способны поглощать частицы, несущие глобальный заряд, не неся при этом глобального заряда, то очевидно, что эти процессы сопровождаются нарушением симметрии, ассоциированной с этими глобальным зарядом.

Можно параметризовать эффект нарушения глобальных симметрий гравитационными взаимодействиями, добавив к низкоэнергетическому лагранжиану неперенормируемые члены, содержащие

обратные степени планковской массы M P1 ~ 1019 ГэВ. Эти члены

должны быть построены так, чтобы точно нарушать рассматриваемые симметрии. Итак, полный лагранжиан теории, помимо вклада стандартной модели, будет включать эффективные неперенормируемые взаимодействия, содержащие операторы Οn , нарушающие

глобальные симметрии стандартной модели

Lэфграв.взаим = ∑	Οn	.	(5.124)
	n
n	M Pl
В этом лагранжиане размерность операторов Οn			равна n + 4.

Поскольку M P1 ~ 1019 ГэВ >> ( 2GF )−1/2 ~ 250 ГэВ, то наивно

можно было бы ожидать, что взаимодействие (5.124) важно только на сверхтяжелых масштабах. Это утверждение оказывается правильным для взаимодействий самих по себе, но неверным при рассмотрении влияния взаимодействия (5.124) на намбуголдстоуновский сектор. Чтобы продемонстрировать первое утверждение, рассмотрим пример (B+L) нарушения. Доминирующее d = 6 (B+L)нарушающее взаимодействие, индуцируемое гравитацией, схематически имеет следующую форму

L	~	1	ucd		ucef		.	(5.125)
		(M Pl )2
(B+L)−наруш			i	j	k	ijk

Такой лагранжиан приводит ко времени жизни протона в процессе p → e+π0 :

τ( p → e+π0 ) ~ (M p )4 ~ 1046 лет.

(5.126)

Это значение гораздо больше современного экспериментального ограничения на время жизни протона. Таким образом, нарушение

203

(B+L) вследствие гравитационных эффектов действительно несущественно.

Другая ситуация, однако, при рассмотрении намбу-голд- стоуновского сектора. Обратимся снова к примеру спонтанного нарушения лептонного числа, сопровождаемого майороном. К сохраняющему лептонное число потенциалу, в котором SU(2)×U(1) синглетное поле σ приобретает VEV, нужно добавить неперенормируемые, нарушающие лептонное число члены, индуцируемые гравитационными взаимодействиями. Простейший из таких членов содержит оператор размерности 5:

V

σ+σ −

V 2

2

λ′

(

σ+σ

)

2

σ + σ+ .

(5.127)

= λ

−

полн

2

M Pl

Первый член в этом потенциале инвариантен относительно преобразования лептонного числа σ → e−2iaσ . Однако это не так для второго члена, который ~ M Pl−1 . Записывая, как и раньше

	V		χ
σ ≈		exp i			,	(5.128)
	2
			V

обнаруживаем, что эффект включения гравитационных поправок сводится к появлению массы намбу-голдстоуновского поля χ. Масса майорона

2		λ′		2		V
mχ	=		V				.	(5.129)
		2 2
						M

Заметим, что величина массы майорона зависит от V – масштаба спонтанного нарушения лептонного числа. Например, если взять

		V	1/2
V ~ ТэВа, то	mχ ~ V		≈10 КэВ. Если V принимает большое
		M p
значение, то масса майорона растет
		m	~ 10		V	3/2	кэВ.	(5.130)
		χ
					ТэВ

Очевидно, если майорон массивный, то некоторые его свойства значительно изменяются. Например, может оказаться, что распад νi → ν j χ будет кинематически подавленным. Конечно, такое воз-

204

можно только в предположении о нарушении симметрии лептонного числа оператором размерности 5. Если нарушение происходит за счет оператора размерности d, то масса майорона

			d −4
	V		2
mχ ~ V			,
	M p

т.е. с ростом d масса становится меньше. Эти рассмотрения вносят трудности в

(5.131)

U (1)PQ решение пробле-

мы сильного СР-нарушения. Гравитационные эффекты не только дают вклад в массу аксиона, но и способны изменить КXД потен-

циал так, что θ не будет стремиться к нулю! Можно пояснить, что происходит с эффективным аксионным потенциалом как в отсутствии, так и в присутствии U (1)PQ нарушающих гравитационных

взаимодействий.

В отсутствие гравитации, физический эффективный гравитационный потенциал можно записать в виде

V	= −Λ4	cos		aфиз	.	(5.132)
аксион	KXД			f

	Этот потенциал обладает условием периодичности по	aфиз			,
			f

имеет минимум при 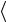aфиз = θэф = 0 и приводит к массе аксиона

ma = Λ2KXД / f .

Включение гравитационных взаимодействий состоит в добавлении к этому потенциалу операторов различных размерностей

Vакс. = −Λ4KXД cos	aфиз		Сf d	aфиз
		−				− δ .	(5.133)
	f		d −4		f
			M Pl

В этом выражении С – безразмерная константа, δ-СР – нарушающая фаза, которая входит посредством гравитационных взаимодействий. Потенциал (5.149) изменяет формулу для массы аксиона

ma2	≈	ΛKX4		Д	+	cf d −2	.	(5.134)
		f	2			M Pld −4
			205

Для величины f в области значений, рассматриваемых в моделях невидимого аксиона, второе слагаемое в выражении (5.133) доминирует над КХД массой аксиона, если не окажется чрезвычайно малой, и (или) размерность d довольно большой.

Проблема в том, что Vакс не имеет минимума при 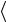aфиз = 0 . Минимум у Vакс оказывается при

		aфиз	≈ csin δ	f d
θэф =						.	(5.135)
		f		M Pld −4ΛKX4
					Д

Таким образом, гравитационные эффекты (при условии, что СР- нарушающая фаза связана с ними), индуцируют ненулевые θ даже в присутствии U (1)PQ симметрии!

Чтобы удовлетворить ограничению θ ≤10−10 , необходимо, чтобы d было большим и (или) константа чрезвычайно малой.

Следует заметить, что ясного разрешения этой проблемы нет, и это в значительной степени осложняет киральной решение сильной СР-проблемы, Однако какое-либо понимание свойств квантовой гравитации отсутствует, и это оставляет надежду, что квантовой гравитации эти проблемы будут преодолены.

Некоторые обнадеживающие результаты в этом направлении получены в теории струн.

Если гравитационные эффекты индуцируют значения θ <10−10 , то сильная СР-проблема решается с помощью U (1)PQ симметрии, а масса аксиона приближенно задается КХД.

206

Глава 6 ДИСКРЕТНЫЕ СИММЕТРИИ

6.1. Введение

Напомним (глава 1), что лоренц-преобразования

xμ → x′μ ≡ Λμν xν

(6.1)

сохраняют инвариантность пространственно-временного интервала

x	xμ = r 2 − c2t2 = r′2 − c2t′2 = x′ x′μ .	(6.2)
μ	μ

Это условие приводит к ограничению вида матриц Λμν

η	= Λλ	η	λk	Λk	,	(6.3)
μν	μ			ν

где матричный тензор ημν представляет собой диагональную матрицу

−1
	1		(6.4)
ημν =	1	.
		1
Псевдоортогональность матриц (6.3)
η = ΛT ηΛ ,			(6.5)

позволяет классифицировать Лоренц преобразования в зависимости от знака детерминанта и Λ00

		det Λ ={−+11;		3
			Λ00 = ± 1+ ∑(Λi0 )2 ={≤≥ −+1.1;					(6.6)
				i=1
В результате группа Лоренца разбивается на четыре части
L↑	:	det Λ = +1,	Λ0 ≥1;	L↑ :	det Λ = −1,	Λ0	≥1;
+			0	−		0		(6.7)
L↓ :		det Λ = +1,	Λ0 ≤ −1;	L↓ :	det Λ = −1,	Λ0	≤1.
+			0	−		0

Матрицы преобразований Λ, принадлежащие Λ↑+ образуют под-

группу группы Лоренца. Ее называют собственной ортохронной группой Лоренца. Все другие преобразования в группе Лоренца

207

можно получить из Λ L↑+ , используя два дискретных преобразования Р и Т, характеризуемые матрицами

+1

−1

Pμ =

−1

−1

;

T μ =

+1

+1

,

(6.8)

ν

ν

−1

+1

которые соответствуют пространственной инверсии (Р-четности) и

обращению времени. Очевидно, что если	Λ L↑	, то	PΛ L↑	,
	+		−

PT Λ L↓+ , и T Λ L↓− . Замечательно, что природа инвариантна

только относительно собственных ортохронных преобразований Лоренца. Четность нарушается в слабых взаимодействиях. Это было теоретически показано в 1956 г. Ли и Янгом и вскоре под-

тверждено в опытах Ву и др. Детектирование распада KL0 на π-

мезоны показало, что, по-видимому, обращение времени не является симметрией природы. Это оказалось возможным понять на основе стандартной модели электрослабых и сильных взаимодействий, а также СРТ теоремы, установленной Паули и др. в 1955 г. Чтобы описать эти экспериментальные данные, надо прежде всего понять, как дискретные пространственно-временные преобразования Р и Т действуют на квантовые поля. Кроме того, надо рассмотреть действие преобразования зарядового сопряжения, изменяющего знаки частиц. Начнем обсуждение с четности.

6.2. Пространственная четность

Свойства преобразований четности электромагнитных полей следуют из классических рассмотрений. Сила Лоренца

	F =	dp	= q(E + υ× B) ,	(6.9)
		dt

очевидно меняет знак при преобразованиях четности, поскольку при этом p → −p . Следовательно, поле E – нечетно, а B – четно относительно пространственной инверсии

208

P	P	(6.10)
E(x,t) →−E(−x,t);	B(x,t) →B(−x,t).

Формально это преобразование осуществляется унитарным оператором U(1). Этот оператор преобразует векторный потенциал

Aμ (x,t) в потенциал Aμ (−x,t) . Исходя из соотношения (6.10), легко понять, что

U (P)Aμ (x,t)U (P)−1 = ε(μ)Aμ (−x,t) ,

(6.11)

где символ ε(μ) означает следующее

−1	μ ≠ 0;
ε(μ) ={+1	μ = 0.	(6.12)

Скалярные поля со спином ноль S(x,t) и псевдоскалярные поля P(x,t) относительно преобразований четности являются, соответственно, четными и нечетными

U (P)S(x,t)U (P)−1 = S(−x,t);

(6.13)

U (P)P(x,t)U (P)−1 = −P(−x,t).

Поведение дираковских полей со спином ½ Ψ(x,t) относительно

преобразования Р несколько более сложное. Однако это поведение определяется предположением о том, что уравнение Дирака инвариантно по отношению к этой операции

U (P)Ψ(x,t)U (P)−1 = ηP γ0Ψ(−x,t) .

(6.14)

В этом выражении ηP – фазовый фактор единичной величины ( ηP 2 =1) . Поскольку во все выражения, характеризующие динамику, входят билинейные комбинации полей, то ηP не имеет физического значения, т.е. можно считать ηP =1.

Исходя из соотношения (6.14), можно вывести свойства четности для фермион – антифермионных билинейных комбинаций.

Поскольку

γ0γ0γ0 = γ0 ; γ0γi γ0 = −γi ; γ0γ5γ0 = −γ5 ,

(6.15)

получаем

209

U (P)Ψ(x,t)Ψ(x,t)U (P)−1 = Ψ(−x,t)Ψ(−x,t) −(скаляр)

U (P)Ψ(x,t)iγ5U (P)−1 = −Ψ(−x,t)iγ5Ψ(−x,t) −(псевдоскаляр)

U (P)Ψ(x,t)γμΨ(x,t)U (P)−1 =

(6.16)

= η(μ) Ψ(−x,t)γμΨ(−x,t) −(вектор)

U(P)Ψ(x,t)γμγ5Ψ(x,t)U (P)−1 =

=−η(μ) Ψ(−x,t)γμγ5Ψ(−x,t) − (псевдовектор).

Исходя из этих свойств, сразу получаем, что электромагнитные взаимодействия инвариантны относительно преобразований четности

Wвзаимэлектр = ∫d 4 xAμ (x)Ψ(x)γμΨ(x) P→Wвзаимэлектр . (6.17)

Если вспомнить определение киральности полей ΨL = 12(1−γ5)Ψ(x) ;

ΨR = 12 (1+ γ5 )Ψ(x) , то преобразование четности Р переводит со-

стояние с одной киральностью в другое состояние:

ΨL (x,t) P→γ0ΨR (−x,t); ΨR (x,t) P→γ0ΨL (−x,t) . (6.18)

Очевидно, что кирально ассиметричные слабые взаимодействия будут нарушать четность. Таким образом, в этом секторе стандартной модели пространственная четность нарушена. Сильные же взаимодействия инвариантны относительно преобразований четности. Эти взаимодействия описываются квантовой хромодинамикой, в которой левые и правые кварки являются триплетами по отношению к калибровочной SU(3) группе

qL ~ 3 ; qR ~ 3 ,

(6.19)

и кварки различаются лишь слабыми взаимодействиями. Относительно слабой SU(2) группы электрослабой SU(2)×U(1) теории левые поля ΨL кварков и лептонов образуют дублеты, а правые

компоненты ΨR – синглеты
ΨL ~2; ΨR ~1.	(6.20)

В этом и состоит причина нарушения четности в слабых взаимодействиях.

210