Емелянов Фундаменталные симметрии 2008

gCkij Aiμ ( x) Aνj ( x) → gCkij Ai′μ ( x) A′jν ( x) =

Aμ

( x) + δa

l

( x)C Aμ

( x) +

i

mli m

= gCkij

+

1

∂μδa

( x)

×

g

i

Aν

( x) + δa

( x)C

Aν

( x)

+

×

j

l

mlj

m

≈ gC

kij

Aμ ( x) Aν

( x) +

+

1

∂νδa

j

( x)

i

j

g

+C

(∂μ

δai ( x)) Aνj ( x) +

+

( x))

kij

+(∂νδa j

Aiμ ( x)

μ

ν

μ

ν

+δal ( x) gCkijCmli Am Aj

+ gCkijCmlj Ai

Am .

С учетом антисимметрии структурных констант, имеем

Ckij (∂μδai ) Aνj = Ckji (∂μδa j ) Aiν = −Cijk (∂μδa j ) Aiν ,

Ckij (∂νδa j ) Aiμ = Cijk (∂νδa j ) Aiμ.

(4.120)

(4.121)

При этом последнее слагаемое в (4.118) сокращает второе слагаемое в (4.120). Если учесть соотношение (4.116), то последнее слагаемое в (4.120) можно записать в более удобной форме

последнее слагаемое (4.120) =

gC

kij

C

Aμ Aν

+

−C

jki

C

mil

+

= δal ( x)

mli

m

j

Amμ Aνj =

+gC

C

= gδal ( x)

+CmkiC jil

kmi

jli

Aμ Aν

(4.122)

i

m

= gδa

( x) g

j

, g

m

Aμ Aν

= igδa

( x)C

g

Aμ Aν

=

l

kl

m j

l

jmρ

ρ kl

m j

= gδa

( x)C

jmρ

C

Aμ Aν

= gδa ( x)C

gC

imj

Aμ , Aν .

l

ρkl

m

j

l

ilk

m

j

Окончательно получаем, что при локальных преобразованиях напряженности Fkμν изменяются следующим образом

μν	δa( x)	μν	μν	( x) + δa jCijk Fi	μν	( x).	(4.123)
Fk	( x) →Fk′		( x) = Fk

161

Lloc = L(Dμχα ,χα ) − 14 FkμνFk μν

При этих преобразованиях полевые напряженности изменяются как квантовые поля, относящиеся к присоединенному представлению группы. С помощью выражения (4.123) легко показать, что

FkμνFk μν – G-инвариант. Действительно

FkμνFk μν → Fk′μνFk′μν = (Fkμν ( x) + δa jCijk Fiμν ( x))×

×(Fk μν ( x) + δa jCijk Fiμν ( x)) = FkμνFk μν +

(4.124)

+δa j (Cijk Fiμν ( x) Fk μν ( x) + Cijk FkμνFiμν ( x)) = FkμνFk μν ,

второе слагаемое обращается в ноль из-за антисимметрии структурных констант: Cijk = −C jik .

Суммируем полученные результаты. Плотность лагранжиана L(∂μχα ,χα ) , обладающая глобальной инвариантностью относи-

тельно преобразований группы G, может быть локальноинвариантной, если ввести в теорию калибровочные поля Aiμ , содержащиеся в ковариантных производных Dμχα и полевых напряженностях Fkμν . Локально-инвариантная плотность лагранжиана:

(4.125)

полностью определяется глобально инвариантным лагранжианом L.

Как и в абелевом случае, массовый член полей Aiμ в лагранжиа-

не недопустим в силу локальной инвариантности (4.113). Чисто калибровочная часть лагранжиана

L = −	1	F μνF	,	(4.126)
	4 k k μν

содержащая кинетический член калибровочных полей Akμ , является нелинейной теорией поля, поскольку содержит квадратичные члены по полям Aiμ . Для абелева случая, когда структурные константы обращаются в ноль, нелинейные члены отсутствуют.

162

Так как калибровочные поля преобразуются нетривиально относительно группы G, то «симметрийные» токи теории (4.125) содержат вклад от калибровочных полей

J μ =

∂L 1

( g

)

χ

+

∂L 1

( g

)

A

.

(4.127)

∂∂μχα i

∂∂μ Aνj i

i

i

αβ

β

i

jk

νk

4.5. Механизм Хиггса

Как уже обсуждалось выше, глобальные симметрии могут быть реализованы вигнер-вейлевским или намбу-голдстоуновским способом, в зависимости от того, изменяется или нет вакуумное состояние при этих преобразованиях. Что происходит, если глобальная симметрия локализуется, и появляются калибровочные поля?

Ввигнер-вейлевском случае ничего не происходит. Помимо вырожденных мультиплетов глобальной симметрии имеется вырожденный безмассовый мультиплет возбуждений калибровочных полей.

Внамбу-голдстоуновском случае происходит замечательная вещь! Когда глобальная симметрия локализуется, голдстоуновские бозоны, ассоциированные с нарушенными генераторами, исчезают, а соответствующие калибровочные поля приобретают массу. Это знаменитый механизм Хиггса.

Чтобы понять суть этого явления, полезно вновь вернуться к U(1) модели. Напомним, что плотность лагранжиана в этой модели

	+		μ			+		1		2
L = −∂μϕ		∂		ϕ− λ	ϕ		ϕ −		f	,	(4.128)
								2

знак величины f определяет вигнер-вейлевскую (f < 0) или намбуголдстоуновскую (f > 0) реализацию симметрии. Чтобы лагранжиан (4.128) стал локально U(1) инвариантным, достаточно заменить ∂μϕ ковариантной производной Dμϕ, содержащей калибровочное

поле Aμ , и включить кинетический член этого поля.

При локальных U(1) преобразованиях

ϕ( x) → ϕ′( x) = eiα(x)ϕ( x);

	Aμ ( x) → Aμ′ ( x) = Aμ ( x) +	1	(4.129)
			∂μα( x).
		g
	163

Ковариантная производная
Dμϕ = (∂μ −igAμ )ϕ.
Следовательно, лагранжиан имеет вид
L = −(Dμϕ+ )(Dμϕ) − λ ϕ+ϕ−					1		f 2	−	1	F μνFμν
					2				4
F μν = ∂	μ	A	− ∂	ν	A		,
		ν			μ

и он, очевидным образом, локально U(1) инвариантен.

(4.130)

(4.131)

Если f < 0 и глобальная симметрия реализована вигнервейлевским образом, то лагранжиан (4.131) описывает взаимодействие вырожденного мультиплета скалярных полей (φ и φ+) между собой, а также взаимодействие с безмассовым калибровочным полем Aμ . Последние взаимодействия содержат как линейный член

по калибровочным полям

L(1)	= gA i	(	∂μϕ+	)	ϕ −iϕ+∂μϕ	= gA J μ,	(4.132)
int	μ					μ
так и взаимодействие типа
	L(1) = −g				2 Aμ A ϕ+ϕ.		(4.133)
					μ

Если же f > 0, т.е. глобальная симметрия реализована намбуголдстоуновским образом, то можно параметризовать теорию в терминах полей с нулевыми вакуумными средними. При такой параметризации оказывается возможным учесть осцилляции вблизи минимума потенциала V(φ). Действительно, заменим

φφ+ = f / 2 + квантовые поля.

(4.134)

Сдвиг за счет этого слагаемого в лагранжиане (4.133) приводит к появлению массового члена поля Aμ

L	= −g 2	f	Aμ A	≡ −	1	m2	Aμ A .	(4.135)
mass	2		μ		2 A		μ

Если калибровочное поле приобретает массу, оно не может быть поперечным (как фотон), у него появляется продольная поляризационная компонента. Эту дополнительную степень свободы надо откуда-то «взять». Нетрудно увидеть, что эта степень свободы возникает за счет намбу-голдстоуновского возбуждения, появляющегося при спонтанном нарушении глобальной U(1) симметрии.

164

Чтобы проверить это утверждение, удобнее всего в случае f > 0 ввести новую параметризацию поля φ

		1				ξ( x)
	ϕ( x) =			f + ρ( x) exp i		f		,	(4.136)
		2

где ρ(х) и ξ(х) – вещественные поля, причем ξ(х) – фазовое поле, связанное с голдстоуновским бозоном. Поле ξ(х) не входит в потенциал, поскольку

		+		f	2		ρ2			2
V = λ	ϕϕ		−			= λ		+	f ρ	,	(4.137)
				2			2
а ρ-поле имеет массу

m2	= 2λf .	(4.138)
ρ

Легко видеть, что фазовое поле ξ входит в ковариантную производную тривиальным образом, т.е. его можно исключить из кинетического члена путем выбора калибровки. Таким образом, намбуголдстоуновский бозон не играет роли в локальной теории. Он «поглощается» и формирует массу калибровочных полей. Действительно, найдем ковариантную производную Dμϕ в параметризации

(4.136) поля ϕ

		1		ξ
	Dμϕ = (∂μ −igAμ )ϕ = (∂μ −igAμ ) ×		( f + ρ)exp i			=
		2		f

ξ

∂μρ −ig(

f

+ ρ) ×

(4.139)

exp i

f

=

∂μξ

.

2

× Aμ −

g

f

Очевидно,

что

фактор

перед

[….]

в

(4.139), включающий

ξ

, не возникает в лагранжиане (4.131), так как в этот ла-

exp i

f

(D ϕ)+ Dμϕ. Кроме того, ξ – зависимость выра-

гранжиан входит

μ

жения в {…..} скобках также иллюзорна, поскольку ее можно исключить путем калибровочного преобразования поля Aμ

165

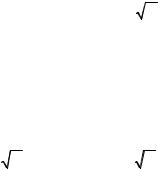
Aμ → Bμ = Aμ −	1		∂μξ	.	(4.140)
	g		f

Если U(1) глобальная симметрия спонтанно нарушена (f > 0), то лагранжиан (4.131) можно переписать в терминах массивного век-

торного поля B′μ и массивного вещественного скалярного поля ρ. Результирующий лагранжиан

L = −

1

∂

μ

ρ∂μρ −

1

m2ρ2

−

1

F μνF −

1

m2 BμB −

2

2

2

ρ

4

μν

A

μ

−g 2

ρ2 BμB

− λ

f ρ3

+ ρ4

(4.141)

f ρ +

,

2

μ

4

где

m2

= 2λf ;

m2

= g 2 f .

(4.142)

ρ

A

Выше показано поглощение голдстоуновского бозона и возникновение массивного калибровочного поля в абелевом случае, однако то же явление происходит и в неабелевом случае.

4.6. Голдстоуновский бозон и лоренц-инвариантность

Знаменитая теорема Голдстоуна подразумевает присутствие возбуждения с нулевой энергией при спонтанном нарушении непрерывной симметрии. В контексте квантовой теории поля этому возбуждению соответствует безмассовая голдстоуновская частица. В случае внутренних симметрий их спонтанное нарушение порождает безмассовые, бесспиновые голдстоуновские бозоны. Спонтанное же нарушение суперсимметрии связано с возникновением безмассовых фермионов со спином ½ – голдстино. Чтобы получить голдстоуновский бозон со спином 1, нужно потребовать нарушения лоренцовской симметрии. Обсудим связь между векторным голдстоуновским бозоном и лоренц-инвариантностью. Оказывается, что в теориях с дополнительными измерениями возможно возникновение векторного голдстоуновского бозона без нарушения 4-мерной лоренцевской симметрии.

166

4.6.1. Голдстоуновские частицы со спином 0 и ½

Предположим, что плотность лагранжиана теории инвариантна относительно непрерывных преобразований, приводящих к сохраняющемуся току,

∂μJμ(x) = 0 .

(4.143)

Это означает, что сохраняющийся заряд является генератором преобразований симметрии

	Q = ∫ J0 (x)d 3x,	dQ	= 0	(4.144)
		dt

Предположим, что имеются два локальных оператора А и В, связанные генератором преобразований симметрии Q соотношением

[Q, A] = B .

(4.145)

Если по некоторым динамическим причинам оператор В имеет ненулевые вакуумные средние (VEV)

0		B		0 >≠ 0 ,	(4.146)

то в этом случае говорят о спонтанном нарушении симметрии. Из (4.145) следует, что

Q		0 ≠ 0 ,	(4.147)

т.е. вакуум уже неинвариантен относительно преобразований сим-

метрии. Теорема Голдстоуна утверждает, что существует состояние

g ( pG

, для которого

Eg ( p) → 0

при

K

(4.148)

p → 0 .

В этих выражениях

p –

импульс частицы. Согласно релятивист-

скому соотношению,

E =

G

2

+ m

2

,

это означает существование

p

безмассовой частицы. Заметим,

что

голдстоуновское

состояние

G

связано с операторами А и Jμ

g ( p

K

K

< 0

Jμ

g( p) >≠ 0;

< 0

A

g( p) >≠ 0 .

(4.149)

Это означает, что голдстоуновское состояние g ( p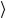 является кван-

том локального оператора А.

Простой пример голдстоуновского бозона со спином 0 – спонтанное нарушение киральной симметрии в низкоэнергетической

167

физике адронов. В этом случае киральный заряд пионные поля πb в скалярном σ поле

Qaπb		= δ	ab	σ .
5

Q5a преобразует

(4.150)

Предположим, что эффективное взаимодействие между π и σ имеет вид

Vэф =

μ

K

2

+ σ

2

) +

λ

(

K2

+ σ

2

)

2

.

(4.151)

2

(π

4

π

Взаимодействие

инвариантно

относительно

киральных

SU (2)L ×SU (2)R

преобразований.

Минимизация Vэф

приводит к

ненулевому VEV поля σ

0

σ

0

=

μ2

.

(4.152)

λ

В этом случае пионные поля π , являющимися партнерами σ при киральном преобразовании (4.150), оказываются безмассовыми голдстоуновскими бозонами. С точки зрения KXД, поле σ представляет собой билинейную комбинацию qq , и соотношение

(4.152) эквивалентно
0 qq 0 ≠ 0 ,	(4.153)

а голдстоуновские бозоны оказываются связанными состояниями

πaqγ5τaq .

(4.154)

При спонтанном нарушении суперсимметрии (см. главу 7) существуют две возможности, одна из них связана с киральным суперполем и антикоммутационным соотношением

{Qξ,Ψ} = 2F ,

(4.155)

где Qξ – суперзаряд, который преобразует фермионы в бозоны и

т.д., Ψ – фермионная компонента, F – скалярная аксиальная компонента кирального суперполя. Если F имеет ненулевое VEV

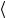0 F 0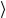 , (4.156)

то фермион ψ становится голдстоуновской частицей (голдстино) и партнером массивного физического скалярного поля. В случае спонтанного нарушения, за счет векторного суперполя, антикоммутационные соотношения

168

{Qξ,λ} = 2D ,

(4.157)

где λ – фермионная компонента, D – аксиальная скалярная компонента векторного суперполя. Если D имеет ненулевое VEV

0		D		0 ≠ 0 ,	(4.158)

то λ становится голдстоуновским фермионом и партнером массивной физической векторной частицы.

4.6.2. Векторный голдстоуновский бозон

Во всех случаях, рассмотренных выше, поля с ненулевыми VEV имеют спин 0, и голдстоуновские частицы являются партнерами этих полей при преобразованиях симметрии.

В 4-мерной теории поля векторное поле не связано с каким-либо скалярным полем. Единственный способ получить векторный голдстоуновский бозон состоит в спонтанном нарушении лоренцевской инвариантности.

По аналогии с соотношением (4.144) предположим, что существуют два векторных поля, связанные некоторым преобразованием симметрии

Q, Aμ		= Bμ .	(4.159)

Если Bμ имеет ненулевые VEV

0		Bμ		0 ≠ 0 ,	(4.160)

то квант поля Aμ будет безмассовой голдстоуновской частицей со спином 1. Очевидно, что условие нарушения симметрии (4.159) нарушает и лоренцовскую инвариантность. Несмотря на то, что существуют строгие экспериментальные ограничения на возможное нарушение Лоренц-симметрии (см. главу 9), весьма интересно рассмотреть эту возможность. В теориях с дополнительными измерениями, однако, оказывается возможным получить векторный голдстоуновский бозон без нарушения лоренцевской симметрии в 4-х измерениях.

169

Рассмотрим векторное поле в 5-мерной теории ϕA , А = 0, 1, 2, 3,

4. По аналогии с (4.150) запишем эффективный потенциал взаимодействия

V (ϕ) =	μ2		(ϕAϕA ) +			λ	(ϕAϕA )2	(4.161)
	2					4
При μ2 > 0
< 0			ϕu		0 >=	μ2		(4.162)
						λ

минимизирует потенциал V (ϕ) . При этом нарушается 5-мерная лоренц-симметрия SO(4,1) до 4-мерной SO(3,1). В результате 4-мерное векторное поле ϕμ , μ=0, 1, 2, 3 оказывается безмассовым

векторным голдстоуновским бозоном. Условие (4.161) можно записать в терминах фермионного конденсата

0				=V δA4 .	(4.163)
		ΨγAΨ

В этом случае векторный голдстоуновский бозон представляет собой составное поле Ψγ AΨ , μ=0,1,2,3.

4.6.3. Голдстоуновский фотон

Еще 40 лет назад Бьеркен обсуждал безмассовость фотона не как следствие калибровочной инвариантности, а как результат спонтанного нарушения симметрии. Эта идея оказалась, в силу успехов калибровочных теорий, не столь притягательной, однако феноменологически она вполне приемлема. Как было отмечено выше, в 4-х измерениях рассмотрение фотона как векторного голдстоуновского бозона требует нарушения лоренц-инвариантности.

Рассмотрим для простоты самовзаимодействующую фермионную полевую теорию с лагранжианом

∞
L = ψ(iγμ∂μ − m) ψ + ∑λ2n (ψγμψ) 2n ,	(4.164)

n=1

170