Емелянов Фундаменталные симметрии 2008

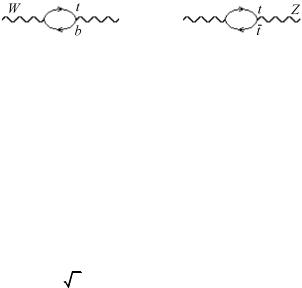
		11G	F	M 2 sin2		θ	W		m2
ρˆ	1−				Z			ln	h	.	(3.87)
					2π2
			24						M Z2

Эта поправка в пределе g′→0 исчезает (так как sin2θW→0). Как видно из соотношения (3.87), лидирующая поправка пропорциональна lnmh , и это даёт возможность получить ограничение на массу хиггсовского бозона из прецизионных электрослабых измерений. Симметрия хиггсовского сектора позволяет понять, какой вклад в параметр ρ вносят массивные фермионы (рис. 3.3)

Рис. 3.3

Лидирующая поправка к величине ρ за счёт петель t и b-кварков

3G

F

2

2

m2m2

m2

ρˆ ≈1+

t

b

t

mt

+ mb

− 2

ln

(3.88)

8 2π2

m2

+ m2

m2

t

b

b

позволила получить оценку массы t-кварка до его экспериментального открытия.

Попытаемся развить эффективную полевую теорию нарушения электрослабой симметрии, в которой проявилась бы симметрия хиггсовского сектора. Для этого заменим матричное поле Φ другим матричным полем Σ, содержащим голдстоуновские бозоны πi (которые “съедаются” слабыми векторными бозонами), но не содержит физического хиггсовского бозона:

		υ		iσπ
	Φ →		Σ ; Σ = e	υ	.	(3.89)
		2

Лагранжиан нарушения электрослабой симметрии аналогичен

(3.71):

L =	υ2	tr(D Σ)+ DμΣ .	(3.90)
	4	μ

При этом матрица полей голдстоуновских бозонов преобразуется следующим образом:

131

SU(2)L: Σ→LΣ

SU(2)R: Σ→ΣR+ (3.91)

SU(2)L+R: Σ→LΣL+

Поскольку SU(2)L×SU(2)R-симметрия реализована нелинейно, эта модель называется нелинейной сигма-моделью. Это означает, что симметрия нарушена. В унитарной калибровке Σ=1, и лагранжиан (3.90) приводит к правильным значениям масс вектроных бозонов

(3.86).

3.4.Калибровочная симметрия и массы частиц стандартной модели

Механизм нарушения электрослабой симметрии неизвестен, поэтому, не обсуждая существование хиггсовского бозона, рассмотрим минимальную модель с одним хиггсовским бозоном. Именно такую модель называют стандартной. Как обсуждалось выше, стандартную модель можно рассматривать как лидирующий член в лагранжиане (3.55) при разложении по обратным степеням большого масштаба M. Имеются, по крайней мере, три причины, чтобы масштаб M был гораздо больше электрослабого масштаба υ:

1) масса майорановского нейтрино ~ υ2 , т.е. M~1014÷1016 ГэВ;

M

2) модели большого объединения указывают на то, что калиб-

ровочные константы должны объединиться на масштабах

~1016 ГэВ.

3) эффекты квантовой гравитации становятся существенными на масштабе планковской массы M Pl ~ GN−1/2 ~ 1019 ГэВ. Возникает

вопрос: если фундаментальный физический масштаб столь велик, почему стандартная модель “действует” при обычных энергиях, а не на масштабах M? В рамках стандартной модели можно найти ответ на этот вопрос, хотя он не является полным.

Начнём с фермионов. Как известно, фермионы преобразуются по комплексному представлению калибровочной группы симметрии. Нет фермионов, которые были бы калибровочными синглета-

132

ми или преобразовались бы по вещественному представлению. По- этому-то майорановские массы оказываются подавленными. Поскольку нет пар фермионов, которые бы преобразовывались как комплексно-сопряжённые представления калибровочной группы симметрии, то и дираковские массы подавлены. Таким образом, фермионы остаются безмассовыми до тех пор, пока не нарушена SU(2)L U(1)Y-симметрия. В этом случае массы фермионов ~0(ν). Хотя это рассмотрение и объясняет, почему фермионы гораздо легче по сравнению с масштабом M, оно недостаточно. В самом деле, только масса t-кварка ~0(ν), все другие заряженные фермионы гораздо легче. В стандартной модели это происходит потому, что юкавские константы связи очень малы. И это весьма загадочно. Например, для электрона юкавская константа связи ~10–5! Малость этих констант означает приближённую симметрию по ароматам. Выше уже отмечалось, что в лидирующем порядке эффективной теории масса нейтрино равна нулю из-за случайной симметрии лептонного числа. Эта симметрия нарушается оператором размерности 5 в соотношении (3.56), при этом нейтрино приобретает ма-

лую массу		υ2		. Кроме фермионных масс, сектор ароматов
	~	M

включает матрицы смешивания СКМ. Углы смешивания в кварковом и нейтрином секторах содержится в табл. 3.2.

		Таблица 3.2
Угол	Кварк	Лептон
θ12	13°	34°
θ23	2,3°	45°
θ13	0,23°	≤12°
δ	60°	неизвестен

Стандартная модель не объясняет иерархии масс и смешивания. Считается, что за эти эффекты “ответственна” физика вне стандартной модели.

Обратимся теперь к калибровочным бозонам. Калибровочные бозоны связаны с локальной (калибровочной) симметрией, обеспечивающей их безмассовость. При калибровочных преобразованиях поля калибровочных бозонов изменяются следующим образом:

133

	TA	→UTA U −1	+	i	(∂	U )U + ,	(3.92)
				g
	μ	μ			μ

где T A – генераторы группы. Второе слагаемое в этом преобразовании подавляет массовый член в лагранжиане

L =	1	M 2 A Aμ = M 2tr(TA TAμ ) ,		(3.93)
	2	μ	μ

причём tr(T AT B ) = 12 δAB .

Калибровочные бозоны связаны с локальной симметрией, однако пока нельзя однозначно ответить на вопрос: они безмассовые вследствие локальной симметрии или локальная симметрия имеет место из-за их безмассовости?

Из-за важности этого вопроса обсудим более подробно связь между безмассовостью калибровочных бозонов и калибровочной симметрией. Для простоты рассмотрим случай квантовой электродинамики, хотя результаты в неабелевых калибровочных теориях вполне аналогичны. Калибровочная симметрия подразумевает вы-

полненеие тождества Уорда для собственной энергии фотона Πμν:

	(3.94)
Тождество Уорда имеет вид
qμΠμν = 0 ,	(3.95)

где q – 4-импульс фотона.

Это условие означает, что собственная энергия должна иметь следующую форму:

Πμν = (q2 gμν − qμqν)Π(q2 ) .

(3.96)

Можно вычислить влияние собственной энергии фотона на фотонный пропагатор, суммируя вклад диаграмм:

Обычно это делается в калибровке Ландау:

134

i

μν

qμqν

i

μρ

q

μqρ

−

g

−

−

g

−

i ×

q2

q2

q2

q2

×(q2 gρσ − qρqσ )Π

(−i)

q

σ

q

ν

gσν −

+... =

q2

q2

= −

i

g

μν

−

qμq

ν

1+ Π +...

=

(−i)

g

μν

−

qμqν

2

2

2

2

q

[

]

[

q

q

]

q

1− Π

Таким образом, пропагатор приобретает фактор [1–П]–1. Найдём вклад в П от фермионной петли:

iΠ

μν

= i(q2 g

μν

− q q

ν

)Π = (−ieQ)2 i2

(−1) ×

μ

d

N

K

ˆ

ˆ

+ qˆ + m)

×∫

trγμ(k

+ m)γν(k

,

(2π)

N

(k

2

− m

2

)((k + q)

2

− m

2

)

(3.97)

.

(3.98)

где Q-фермионный электрический заряд и фактор (-1) возникает изза фермионной петли. Вычислим интеграл в N измерениях и выде-

лим ультрафиолетовые расходимости. Сворачивая обе части (3.98) с gμν, получим

i(q2 N −q2 )Π = −e2Q2 ×

d

N

K

ˆ

ˆ

+ m)

(3.99)

×∫

trγμ(k

+ m)γν(k + qˆ

.

(2π)

N

(k

2

−m

2

)((k + q)

2

−m

2

)

При этом мы воспользовались соотношением gμνgμν=N.

Вычисление следа даёт:

ˆ

μ

ˆ

=

trγμ (k + m)γ

(k + qˆ + m)

(3.100)

= 4

−2(1− ε)(k 2 + kq) + (4 − 2ε)m2

,

где использованы соотношения

γμγμ = N ≡ 4 − 2ε;

γμqˆγμ = −2(1− ε)qˆ.

(3.101)

Перепишем теперь числитель в интеграле через факторы, появляющиеся в знаменателе:

	k 2 + kq =	1	× (k +1)2	− m2 + (k 2	− m2 ) − q2	+ 2m2 .	(3.102)
		2
				135

Это позволяет представить интеграл в виде:

i(3 − 2ε)q2Π = −4e2Q2 = ∫

d N K

×

N

(2π)

(3.103)

1

1

(1− ε)q2 + 2m2

× (ε −1)

+

+

.

k 2

− m2

(k + q)2 − m2

(k 2

− m2 )((k + q)2 − m2 )

Предположим, что мы работаем в N = 4 измерениях (ε = 0), тогда первые два интеграла в (3.103) квадратично расходятся. Введём для них обрезание по импульсу, тогда первый интеграл в (3.103):

∫

d 4 K

1

= i∫

d 4 KE

1

−

i

M

2

,

(3.104)

(2π)

4

k

2

− m

2

(2π)

4

2

2

)

16π

2

(−KE − m

где проведён

виковский

поворот к

евклидову

пространству

(K 0 → iKE0 )

и d 4 KE = π2 KE2 dKE2

(после интегрирования по углам)

и сделано обрезание при KE2 = M 2 . Второй интеграл в (3.102) даёт

тот же самый результат, если произвести сдвиг K→K–q.

Таким образом

e2

M 2

Π

~

Q2

.

(3.105)

6π2

q2

Подставляя это значение в соотношение (3.97), видим, что фотон приобретает (тахионную) массу ~0(M):

−i			≈				i		.	(3.106)
q2 1− Π	]					e	2
[				q2	+			Q2M 2
						6π2

Где же допущена ошибка? Оказывается, что обрезание нарушает тождество Уорда:

Πμν ~ M 2 gμν → qμΠμν ≠ 0 .

(3.107)

Таким образом, действительно тождество Уорда, которое следует из калибровочной симметрии, обеспечивает безмассовость фотона.

Вместо того, чтобы вводить обрезание, вычислим собственную энергию фотона в N измерениях при соблюдении тождеств Уорда. Квадратично расходятся интегралы

136

∫

d N K

1

=

(2π)

N

k

2

−m

2

(3.108)

d N K

1

i

= ∫

= −

Γ(ε−1)(m2 )1−ε.

(2π)

N

(K +q)

2

−m

2

(4π)

N /2

Полюс при ε=1 (N=2) свидетельствует о квадратичной расходимости, однако эти интегралы умножаются на фактор (ε–1) в выражении (3.103). Поскольку (ε–1)Γ(ε–1)=Γ(ε), то полюс возникает при ε=1, и квадратичная расходимость – всего лишь иллюзия, это артефакт схемы регуляризации, нарушающей тождество Уорда.

Окончательно вычисление собственной энергии даёт:

	8e	2	2	1			x(1− x)
Π = −			Q	Γ(ε)×∫dx							.	(3.109)
			N /2		m	2	− x(1− x)q	2
	(4π)			0						ε

Полюс при ε=0 (N=4) означает наличие логарифмической расходимости. Поставляя П в соотношение (3.97), видим, что фотонный пропагатор, благодаря тождеству Уорда, имеет полюс при q2=0, т.е. фотон остаётся безмассовым. Таким образом, стандартная модель успешно объясняет, почему фермионы и бозоны гораздо легче, чем гипотетический фундаментальный масштаб M. Обратимся теперь к скалярам. В этом случае стандартная модель не столь успешна. Массовый член в лагранжиане для скаляров имеет вид:

L = −m2φ+φ

(3.110)

и не связан с калибровочной симметрией, т.е. нет причин ожидать, чтобы скаляры были гораздо легче по сравнению с M. В стандартной модели это бы означало, что хиггсовское поле имеет массу ~O(M), и при низких энергиях было бы неспособным нарушать электрослабую симметрию. Есть по крайней мере, несколько путей, чтобы избежать этого заключения.

Один путь – ввести скалярные голдстоуновские бозоны некоторой нарушенной симметрии. В другом случае – создать безмассовые скаляры, используя идеи суперсимметрии (см. главу 7).

В стандартной модели электрослабый масштаб, как КХД масштаб Λ, а также массы кварков и лептонов гораздо меньше планковского масштаба, т.е. их можно считать равными нулю. Если это

137

так, то квантовая теория поля, содержащая безмассовые поля, будет конформной теорией. Это предположение означает, что калибровочные бозоны, кварки и лептоны, совместно с неизвестными степенями свободы, способны составить квантовую теорию поля с нетривиальной реализацией конформной инвариантности. В этом сценарии отсутствие значительных массовых поправок есть следствие конформной инвариантности. Можно предположить, что теория описывается действием

S = S0 + ∫d 4 xLiOi ,

(3.111)

где S0 – лагранжиан рассматриваемой теории поля, Oi – операторы размерности, меньше 4, нарушающие конформную инвариантность. Величины Li представляют собой «массовые» параметры.

Пусть М – массовый масштаб, определяемый параметрами Li. Это масштаб нарушения конформной инвариантности. Другими словами, для энергий Е>> М константы связи теории перестают изменяться, а при Е< M такое изменение происходит. Оказывается, если считать М ~ ТэВ’а, то в предположении конформной инвариантности разрешается проблема иерархий (см. главу 7).

138

χα (x) a→χ′α (x) = Rαβ (a)χβ (x) .

Глава 4 ТОЧНЫЕ И НАРУШЕННЫЕ СИММЕТРИИ

В ФИЗИКЕ ЧАСТИЦ

4.1. Введение

Физику частиц можно рассматривать как квантовую теорию поля, в которой фундаментальному возбуждению приписывается соответствующее квантовое поле. Симметрии учитываются при построении плотности лагранжиана, включающего квантовые поля. Действие

S = ∫d 4 xL	(4.1)
при этом инвариантно относительно преобразований симметрии
S →S′=S.	(4.2)

Будем пока рассматривать только непрерывные преобразования симметрии, основанные на группе Ли G. Пусть квантовое поле обо-

значено через χα (x) , где х – пространственно-временная переменная, α – «внутренний» индекс, соответствующий возможным компонентам поля χ. Например, для кварков χα (x) = qα (x) и α=1,2,3. Если а – один из операторов группы G и если квантовые поля χα (x) – члены неприводимого мультиплета, то действие оператора

а

(4.3)

Таким образом, при таком преобразовании поле χ переходит в новое поле χ′, чьи компоненты являются линейной комбинацией «старых» компонент.

Поскольку, по предположению, квантовые поля χ′α – члены

мультиплета группы G, то матрицы R(a) реализуют матричное представление группы G и обладают определенными свойствами.

Если произвести последовательные преобразования

χα (x) a→χ′α (x) a→χ′′α (x) (4.4)

и сравнить с «прямым» преобразованием

139

a′′	(4.5)
χα (x) →χ′′α (x) ,
то получим
Rαβ (a′)Rβγ (a) = Rαγ (a′′) .	(4.6)

В гильбертовом пространстве квантового поля χα преобразование (4.3) осуществляется унитарным оператором U(a). При этом

U −1 (a)χα (x)U (a) = χ′α (x) = Rαβ (a)χβ (x).

(4.7)

Очевидно, что свойство (4.6) для унитарных операторов выглядит так:

U (a)U (a′) =U (a′′) .

(4.8)

Поскольку, мы рассматриваем непрерывные преобразования симметрии, то достаточно ограничиться инфинитезимальными преобразованиями δа. Конечные преобразования строятся с помощью соотношения (4.8). Группа Ли характеризуется набором параметров, ассоциированных с этими инфинитезимальными преобразованиями, или алгеброй операторов, связанной с этими преобразованиями. Запишем инфинитезимальное преобразование в виде:

U (δa) =1+ iδaiGi ,

(4.9)

где индекс i соответствует всем независимым параметрам группы Ли G (для группы вращений О(3) δаi описывают независимые вращения вокруг осей x, y, z). Операторы Gi называются генераторами группы, причем свойство (4.8) подразумевает определенную алгебру этих генераторов. Если считать параметры δаi вещественными, то генераторы Gi будут эрмитовыми. Они образуют алгебру Ли

G ,G		= C	ijk	G	k	.	(4.10)
i	j

Структурные константы Cijk группы можно выбрать полностью антисимметричными по индексам i, j, k. Как U(δa) можно разложить в

терминах генераторов Gi, так и матрицы представления Rαβ(δa) можно подвергнуть этой процедуре. Для инфинитезимальных преобразований

Rαβ (δa) = δαβ + iδai (gi )αβ .

(4.11)

Очевидно, что матрицы gi являются представлениями генераторов Gi, поэтому они тоже удовлетворяют соотношению (4.10). Чтобы

140