Емелянов Фундаменталные симметрии 2008

нальное к v , содержит v . Если u N, запишем u = ∑αav(a) . Так

как Γu N , то	a
Γu = ∑Γabαbv(a) .	(1.85)
ab

Таким образом, матричные элементы Гab определяют Г и наоборот.

Условия Γu Γu′ = u u′ и Γ v = v			подразумевают, что
	cos θ		sin θ	0
Γab	=	−sin θ	cos θ	0	(1.86)
		Γ31	Γ32
				1

с произвольными значениями Г31, Г32. Этот набор матриц имеет структуру, подобную евклидовой группе плоскости: SOz(2)×T2, где

SOz(2) – вращение вокруг оси OZ:				0
cos θ			sin θ
−sin θ			cos θ	0		(1.87)
	0		0	1
и трансляции		1	0	0
T	=	0	1	0	.	(1.88)
2
		Γ31	Γ32	1

В заключение этого раздела сформулируем несколько определений. Световым конусом называется набор векторов для которых v2=0. Если, кроме того, v0 > 0 (v0 < 0), то говорят о переднем положительном (заднем, отрицательном) световом конусе, обозначаемом

V+ (V–). Набор векторов U c u2 = m2 > 0 обозначается Ω±(m), (±) соответствует знаку u0 и называется передним положительным (задним, отрицательным массовым гиперболоидом для u0 > 0 (u0 < 0)). Набор векторов ω, таких, что ω ω = –μ2, μ2 > 0 называется гиперболоидом мнимых масс Ω(iμ).

Нетрудно проверить, что наборы V+, V–, Ω+(m), Ω–(m), Ω(iμ) инвариантны относительно L↑+ , и каждый вектор из одного из этих

наборов получается соответствующим преобразованием любого другого элемента из того же набора.

51

1.2.4. Соответствие L→SL(2, C)

Каждому вектору v с компонентами vμ сопоставим 2×2-компо- нентную матрицу

GG	= ∑gμνσ	v0 + v3	v1 −iv2
v = v0 + σv		μvμ = v +iv	v −v		;
	μν	1 2	0 3

σ0 = σ0 =1; σi = −σi.

Тогда имеем

σμ = ∑gμνσν; trσμσν = 2gμν

ν
det v = v v;	v	=	1 trσ		v; v+ = v,
	μ		2	μ

причем соотношение выполняется, если vμ – вещественны. Для каждого преобразования Лоренца

Λ: v → Λv ≡ vΛ .

(1.89)

(1.90)

(1.91)

имеется соответствующая матрица A SL(2, C). Определим А следующим образом:

AvA	+ = v	= σΛv .	(1.92)
	Λ

На самом деле, обе матрицы ±А соответствуют одному Λ. Точная формула для рассматриваемого соответствия может быть уста-

новлена так: выберем вектора v(α) с vμ(α) = δαμ . Применяя формулу (1.92) к ним, получаем

Λ	βα	=	1	trσ Aσ	a	A+ .	(1.93)
			2	β

Формулу для инверсии получить несколько сложнее. Будем рассматривать отдельно ускорения L(v):

L(v)nt = vi , nt	μ	= δμ0	(1.94)

и вращения R. Для ускорений с учетом n~t =1 и соотношения (1.92) получаем

A(L(v)) A+ (L(v)) = v .

(1.95)

Это уравнение имеет решение

52

A(L(v)) = +v1/2 .

(1.96)

Заметим, что v = L(v)nt – положительно определен. Выберем

знак (+) для корня квадратного в силу непрерывности. Для сдвигов A(L(v))+ = A(L(v)). Для вращений R имеем Rnt = nt, и соотношение

(1.92) дает

A(R)A(R)+ = 1,

(1.97)

т.е. матрица А – унитарна. Пусть θ – набор параметров вращения

R. Для инфинитезимальных

θ и v0 = 0

G

G

G

G

(1.98)

v ≡ σ v

→ σ v + ∑σ jθk vlε jkl .

Если представить

G

GG

(1.99)

A(R) = exp(iθλ)−1+ iθλ ,

то с помощью (1.92) получим

GG

G

)

GG

GG

+

∑

σ

θ

v ε

,

(1.100)

1+ iθλ

σv

1−iθλ

−σv

j

jkl

(

(

)

k l

для которых

λ

j

,σ

= −

∑

ε

jkl

σ

l

,

(1.101)

G

σ

k

и

следовательно, λ = −

2

G

i

GG

A(R(θ)) = exp −

θσ .

(1.102)

2

Если 4-вектор v удовлетворяет условию v2 = 1, v0 > 0, определим ξ следующим образом:

Тогда

и поэтому

cosh ξ = v0; sinh ξ =

vG

,

ξG

=

vGG

.

ξ

v

1/2

ξ

1 G G

ξ

1 G G

v

= cosh

+

ξ σsinh

= exp

ξ σ

2

ξ

2

2

1 GG

A(L(v)) = exp

ξσ .

2

(1.103)

(1.104)

(1.105)

Найдем далее изображения малых групп в SL(2,C). Для времениподобного случая выберем вектор nt c ntμ = δμ0 . Тогда nt = 1,

изображение U вращения R удовлетворяет условию UU+ = 1, т.е.

53

изображением подгруппы SO(3) группы L является подгруппа

SU(2) группы SL(2,C).

Для светоподобных векторов выберем n = nt + n(3), причем nt

выберем, как и раньше, а n(3) = δ	μ3	. Тогда
μ
n =1+ σ3	=	2	0		(1.106)
			0	.
		0

Если N – изображение в SL(2,C) – малой группы преобразования Г: Гu=n, то оно должно удовлетворять условиям:

2

0

+

2

0

det N =1.

N

N

=

0

,

0

0

0

Отсюда следует, что N можно представить в виде

eiθ/2

e−iθ/2

(a + ib)

N =

0

e−iθ/2

.

Введем обозначения

≡ (A−1+ (Λ))

Dαβ(1/2) (Λ) ≡ Aαβ (Λ),

D(1/2

) (Λ)

,

αβ

− σ vG = σ v,

αβ

а также

vˆ = v

v

≡ σΛv.

0

Λ

Легко проверить, что

A−1+vAˆ −1 = vˆ

,

Λ

(1.107)

(1.108)

(1.109)

(1.110)

(1.111)

Эта формула является дополнительной к (1.92), и она определяет другое представление группы L в SL(2,C), неэквивалентное (1.92). Свяжем это представление со стандартным дираковским формализмом. Для этого заметим, что в вейлевской реализации гаммаматриц

				0		σμ		,	σ0 =1			(1.112)
				γμ =	σμ	0
								v
имеем						0						(1.113)
				γ v =				0	.
Далее определим						vˆ
								Aαβ(Λ)
D	Λ =		(1/2)	(Λ)	0						0
			D				=			−1+		. (1.114)
(	)			(	)				0		(Λ))
										(A
			0	D	1/2	(Λ)						αβ
						54

В качестве приложения докажем трансформационные свойства дираковских γ-матриц. В вейлевской реализации для произвольного 4-вектора v:

D

−1

A−1

0 0 v

A 0

=

(Λ)γ vD(Λ) =

0

A

+

−1+

vˆ 0

0 A

0

A−1vAˆ

−1+

0

σΛ−1v

=

(1.115)

=

0

=

σΛ−1v

0

AvAˆ +

0

(Λσ)v

=

(σΛ)v

0

= (Λγ) σ,

где использованы соотношения (1.92) и (1.111).

В силу произвольности v, получаем

D−1 (Λ)γμD(Λ) = ∑Λμνγν .

(1.116)

1.2.5. Конечномерные представления SL(2,C)

Обозначим через М2 алгебру Ли SL(2,C) – она состоит из 2×2 комплексных матриц с нулевыми следами. Если А1 – алгебра под-

группы SU(2) группы SL(2,C), то A1C = M2 . Поэтому представления

группы Лоренца можно получить с помощью представлений группы вращений. В частности, коэффициенты Клебша-Гордона для SU(2) и SL(2,C) – одинаковые. Таким образом, с помощью простого тензорного произведения

Aα β	Aα β	...Aα	Bj	(1.117)
1 1	2	2	j

можно построить представление SL(2,C), которое при ограничении на группу вращений соответствует спину j/2.

1.2.6. Общее описание релятивистских состояний

Во многих приложениях удобно ввести абстрактные характеристики релятивистских состояний. Будем считать, что этим состояниям соответствует импульс p и другие величины, обозначаемые

через ξ (это может быть компонента спина). Задача будет состоять

55

в построении состояний pG, ξ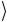 и изучении их трансформационных

свойств при релятивистских преобразованиях. Инвариантной группой в теории относительности является группа Пуанкаре, иногда называемая неоднородной группой Лоренца. Её элементы – пары (a, Λ), где а – 4-мерные трансляции, состоящие из пространственных трансляций на вектор a и временных трансляций на a0 /c , а

также собственного (ортохронного) Лоренц-преобразования Λ. Генераторы группы Пуанкаре включают генераторы вращений, сдвигов и трансляций. Для любого представления U(a,Λ) группы Пуанкаре инфинитезимальные преобразования имеют вид

	G		i	GG	G		i	G G		i
	U (0, R(θ))−	1−		θL,	U (0, L(ξ)) −	1−		ξN, U (a,1) −	1−		a P. (1.118)
		=				=			=

Коммутационные соотношения между генераторами можно определить в любом представлении. Выберем для этих целей регулярное представление, в котором U действует на скалярные функции a, Λ. Тогда

Lj =i=∑εjkl xk∂l ; N j =i=(x0∂ j − xj∂0 ); Pj =i=∂ j ; P0 =i=∂0. (1.119)

Используя эти соотношения, найдем соответствующие коммутаторы:

L , L

= i=

∑

ε

L ;

L , N

= i=

∑

ε

jkl

N

;

k

j

jkl l

k

j

l

=

i=∑

ε

jkl Pl ;

[Lk , P0 ]

=

0;

=

0;

(1.120)

Lk , Pj

Pμ, Pν

[Nk , P0 ] = −i=Pk .

Nk , N j = i=∑ε jkl Ll ;

Nk

, Pj = −i=δkj P0;

Эти соотношения можно записать в ковариантной форме

U (Λ) −1−

i

ωμνMμν .

(1.121)

=

С помощью простого вычисления, используя то факт, что

∂

μ

, x = g

μν

,

(1.122)

ν

получаем для коммутационных соотношений

56

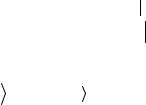
M

μν

,P =i=

g P − g P

;

α

(

να μ

μα

ν)

αμ)

M

μν

,M

=i=

g

M

βν

+ g

M

να

+ g

M

μβ

+ g

νβ

M

;

(1.123)

αβ

(

μα

μβ

να

P ,P

=0.

μ ν

Рассмотрим теперь квантовую систему чье состояние ψ . Пу- анкаре-преобразование g переводит его в новое состояние ψg . В

духе квантовой механики, считаем, что этому переходу соответствует линейный унитарный оператор

U (g) =U (a,Λ),		ψg =U (a,Λ)		ψ .	(1.124)

При этом считаем, что U – представление группы Пуанкаре. На самом деле, представление определяется с точностью до фазы

′ ′	) = e	iϕ	′ ′	) .	(1.125)
U (a,Λ)U (a ,Λ		U (a + Λa ,ΛΛ

Ниже будет построено точное представление для ϕ = 0 . Рас-

сматриваться будут унитарные представления группы Пуанкаре. Поскольку приводимое представление разлагается на ортогональные неприводимые представления, достаточно рассмотреть только неприводимые, они описывают элементарные системы, которые будем называть частицами. Заметим, что здесь термин «элементарность» используется в нединамическом смысле. Он означает лишь, что соответствующая изолированная система не может быть описана как две и более систем, тоже изолированные.

1.2.7.Релятивистские одночастичные состояния. Общее описание

Обозначим через G гильбертово пространство свободных одночастичных состояний. Построим базис G, работая в гейзенберговском подходе. Рассмотрим операторы трансляций U(a,1) ≡ U(a). Если их записать в экспоненциальной форме

U (a) = exp(ia P) ,

(1.126)

то унитарность U подразумевает эрмитовость Рμ. Будем идентифицировать Р0 с оператором энергии (гамильтонианом) и P – с оператором импульса; Рμ образует оператор 4-импульса.

57

Из коммутационных соотношений следует, что оператор Р2 = Р Р коммутирует со всеми генераторами группы Пуанкаре, следовательно, со всеми U (a,Λ) . По лемме Шура, это означает,

что Р2 = const, которую будем идентифицировать с квадратом массы (она может быть равной нулю)

m2 = P P .

(1.127)

Отсюда следует, что для свободной частицы оператор Р0 является
функцией PG
P0 = +(m2 + PG2 )1/2 ,	(1.128)

где выбран положительный знак, чтобы обеспечить положитель-

ность энергии. Если p –	собственные значения оператора	P , то
р0 – собственные значения Р0, и тогда
p	= + m2 + pG2 ,	(1.129)
0

как можно было ожидать для релятивистской частицы.

Как известно, компоненты Рμ коммутируют друг с другом. Их можно диагонализовать и рассматривать как соответствующие собственные векторы в базисе пространства G, который будем обозна-

чать через p;ξ , где ξ – набор квантовых чисел, определяющий состояния. Как будет видно, ξ включает спиновую компоненту.

Поскольку

p;ξ – собственные состояния Рμ, то

Рμ

p;ξ = рμ

p;ξ .

(1.130)

Экспоненциируя и записывая U(a) вместо U(a,1), получим

U (a)

p;ξ = eia P

p;ξ = eia p

p;ξ .

(1.131)

Выберем определенный импульс

p , причем p p = m2 , p

> 0 . Это

0

означает, что выбрана определенная система отсчета. Любой допустимый 4-вектор частицы можно записать в виде

p = Λ( p) p ,

(1.132)

где Λ( p) – преобразование Лоренца (это представление не единственное). Если выбрать для каждого р семейство Λ( p) таких преобразований Лоренца, то базис будет зависеть от выбранного се-

58

мейства Λ( p) . Определим базис Λ( p),ξ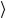 с помощью соотношения

Λ( p),ξ ≡U (Λ( p))		p,ξ .	(1.133)

Покажем, что состояние Λ( p),ξ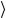 соответствует 4-импульсу Р.

Чтобы это обнаружить, запишем
U (a)				Λ( p),ξ =U (a)U (Λ( p))		p,ξ .			(1.134)
Используя тождество
U (a,Λ( p)) =U (a, Λ( p)) =U (Λ( p)) U (Λ−1 ( p)a), (1.135)
получим
U (a)		Λ( p),ξ =U (Λ( p))U (Λ( p)−1 a)						p,ξ .	(1.136)

Учитывая, что (Λ( p)−1 a) p = aΛ( p) p = a p ,

имеем

U (Λ( p))U (Λ( p)−1 a) p,ξ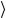 =U (Λ( p))ei(Λ( p)−1ap)

= eip aU (Λ( p)) p,ξ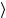 = eip a Λ( p),ξ.

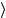Таким образом, показано, что

U (a) Λ( p),ξ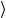 = eia p Λ( p),ξ ,

т.е. Λ( p),ξ – состояние с импульсом р

Pμ Λ( p),ξ = pμ Λ( p),ξ .

(1.137)

p,ξ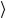 = (1.138)

(1.139)

(1.140)

Это соотношение определяет, как трансляции действуют на базисные вектора Λ( p),ξ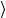 . Выведем теперь соответствующие формулы для лоренцевских преобразований. Начнем с рассмотрения преобразований, которые обозначим через Γ, Γ′,... , содержащиеся в малой группе W ( p) вектора p . Поскольку Г оставляет инвариантным p , то собственный вектор U (Γ) p,ξ 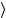, будет соответствовать импульсу p , т.е. он должен быть линейной комбинацией векторов p,ξ′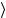

U (Γ)		p,ξ = ∑Dξξ′ (Γ)		′
				p,ξ ,	(1.141)

ξ′

59

где Dξξ′ – определенные коэффициенты. Итак, в случае массивной

частицы со спином ½, параметр ξ будет являться третьей компонентой спина, т.е. ξ = ±1/2 . Легко проверить, что условия

U (Γ)U (Γ′) =U (ΓΓ′), U (Γ−1) =U −1 (Γ),	U + (Γ) =U −1 (Γ)	(1.142)
подразумевают
D(Γ) D(Γ′) = D(ΓΓ′), D(Γ−1) = D(Γ)−1 ,	D+ (Γ) = D(Γ)−1 .	(1.143)

Это означает, что матрицы D реализуют унитарное представление малой группы W ( p) . Конкретная форма матрицы D будет обсуждаться ниже. Здесь же будем считать, что такое представление существует и известны коэффициенты Dξξ′ (Γ) . С их помощью мож-

но разрешить проблему: как действует произвольное преобразование Лоренца? Действительно,

	U (Λ)		Λ( p),ξ =U (Λ)U (Λ( p))			p,ξ =
	=U (Λ(Λ		p))U (Λ(Λp)−1U (ΛΛ−1 ( p)))						p,ξ =	(1.144)
	=U (Λ(Λp))U (Λ(Λp)−1 ΛΛ( p))						p,ξ ,
где Λ(Λp)p = Λp и введен член U (Λ(Λp)) U (Λ(Λp))−1 =1.
Тогда	(Λ(Λp))−1 ΛΛ( p) p = (Λ(Λp))−1 Λp = p ,									(1.145)

т.е. преобразование (Λ(Λp))−1 ΛΛ( p) , которое мы обозначили че-

рез Γ( p,Λ) действительно принадлежит W ( p) , т.к.								оставляет p
инвариантным.
Таким образом, находим
U (Γ( p,Λ))			p,ξ = ∑Dξξ′ (Γ( p,Λ))			′
						p,ξ .		(1.146)
			ξ′
Иначе говоря,
	Λ( p),ξ = ∑Dξξ′ (Γ( p,Λ))					′
U (Λ)				Λ(Λp),ξ			;
			ξ′					(1.147)

Γ( p,Λ) ≡ (Λ(Λp))−1 ΛΛ( p).

60