Емелянов Фундаменталные симметрии 2008

величина с – скорость света в вакууме. В кратких обозначениях преобразования (1.33) можно представить в виде:

G

rG → L(vt )rG,

t → L(vz )t.

(1.34)

ориентирован произвольно, обычно используют та-

Если вектор v

кой трюк. Пусть R(z → v)

–

вращение, переводящее ось OZ в на-

G

правление v . Например, можно выбрать

v

G

G

G

G

R(z ® v) = R(α),

R(α) z =

G

(1.35)

с zG – единичным вектором в направлении OZ

v

и

v3

G

α

G

G

cos α =

,

α =

(sin α)[z

×v

] .

(1.36)

v

v

Обозначив через L( v ) лоренц-сдвиг со скоростью v , определим

L (vG) = R ( zG → vG) L (vGz ) R−1 ( zG → vG) ,

(1.37)

где vGz – вектор длины v вдоль OZ. Используя точные формулы для

L(vz ) и R, находим

vG rG

G

G G

G

G

v2 −1/2

1 G

G

G

r → L

(v ) r

= r

−

v2

v

+

1−

v

r +t

v,

c2

v2

v2 −1/2

1

(1.38)

G

G

G

G

t → L (v ) t

=

1

−

v

r

+ t

v.

Параметры vG

c2

c2

не являются «нормальными»: произведение сдвигов

vG и vG' не дает сдвига v + vG

'

(он не существует, если

v + vG'

≥ c ).

G

G

Удобнее использовать другие параметры ξ, η . Если ξ, η парал-

лельны, то

G

G

G

(1.39)

G

L (ξ) L (η) = L (ξ+ η) .

Выберем ξ вдоль OZ. Если записать

L (ξ)

z = A(ξ) z + B (ξ) ct,

(1.40)

L (ξG)

t =

1

C (ξ) z + D (ξ)t,

c

41

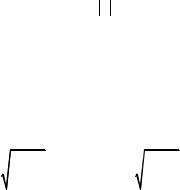
где А, В, С, D – функции, которые необходимо определить и которые удовлетворяют условиям

AB = CD, A2 −C 2 = D2 − B2 =1.
Введем функцию ϕ(ξ)	с помощью соотношений
A = D = cosh ϕ(ξ), B = C = sinh ϕ(ξG).
Эти соотношения подразумевают, что		G	G
	G
cosh (φ(ξ) + φ(η)) = cosh (φ(ξ))cosh (φ(η)) +
	G	G
+sinh (φ(ξ))sinh		(φ(η));
G	G	G	G
sinh (φ(ξ) + φ(η)) = cosh (φ(ξ))sinh (φ			(η)) +
	G	G
+sinh (φ(ξ))cosh (φ(η)),

поэтому можно выбрать ϕ(ξ) = ξ = ξ . Окончательно x → x; y → y′;

(1.41)

(1.42)

(1.43)

z → (cosh ξ) z + (sinh ξ) ct;

(1.44)

t →

1

(sinh

ξ) z + (cosh ξ)t;

ξG|| OZ.

c

Соотношение между ξ и v определяют выражения

1

vG

1

G

G

cosh ξ =

; sinh ξ =

, ξ

|| v .

(1.45)

1− v

2

c

− v

2

1

c2

c

2

Величину ξ обычно называют быстротой. Для произвольного сдви-

G

га ξ находим

G

G

G

G

G

G

G

1

ξ r

rG

→ L (ξ) rG = rG −

ξ 2r

ξ +

(cosh ξ)

ξ + c (sinh ξ)tξ ;

ξ

ξ

ξ

(1.46)

G

1 sin ξ G

G

t → L (

ξ)

t = (cosh ξ)t +

ξ r.

c

ξ

G

G

<< c

v

Для

v

ξ = c

,

(1.47)

поэтому лоренцевский сдвиг совпадает с галилеевым сдвигом.

42

Преобразования Λ набора (r, t ) – вращения и сдвиги
Λ = LR,	(1.48)

называются преобразованиями Лоренца. Как будет видно ниже, они образуют группу, называемую группой Лоренца или ортохронной собственной группой Лоренца. Если включить возможные произведения пространственных и временных отражений

Is : r → −rG, t → t;	It : rG → rG, t → −t,	(1.49)
получим полную группу Лоренца. Её элементы имеют вид
LR, IsLR,	It LR, IsIt LR .	(1.50)

1.2.2.Пространство Минковского. Полная группа Лоренца

Как было показано выше, лоренцевские сдвиги смешивают пространство и время. Единое трактование релятивистских преобразований требует, чтобы мы работали с набором величин, содержащих как пространственные, так и временные характеристики. Такую возможность дает пространство Минковского. Его элементы (или точки), обозначаются буквами x, у,... называются 4-векторами и

определяются четырьмя координатами xμ (μ = 0, 1, 2, 3)

x0
x		,	(1.51)
x ~ 1
x2
x
3			j = 1, 2, 3 – про-
где x0 = ct – временная координата, а x j = rj ,

странственные координаты.

Обычно координаты пространства Минковского обозначают греческими индексами μ, ν = 0,…, 3; латинские индексы i, j изменяются от 1 до 3. Иногда обозначают через r пространственную часть x

ct		(1.52)
x ~	G .
	r

43

Лоренцевские сдвиги можно представить посредством 4×4 матриц L, x → Lx с элементами Lμν . При этом

3

(Lx)μ = ∑ Lμνxν .

В явном виде

ν=0

3

(Lx)0 = (cosh ξ) x0

+

sinh ξ

∑ξ j x j

ξ

j=1

(Lx)

1

3

1

3

i

= x

−

ξ

j

x

ξ

i

+

cosh ξ

ξ

j

x

+ x

0

sinh ξ

ξ

.

2

i

ξ

∑

j

ξ

∑

j

i

j=1

j=1

(1.53)

(1.54)

Вращения, определяющие преобразования пространства Минковского: x → Rx

(Rx)μ = ∑Rμνxν;

(Rx)0 = x0

ν

(1.55)

(Rx)

=(cos θ) x

1−cos θ

∑

sin θ

∑

+

θ

x

θ +

ε

θ

x .

i

2

j

ikl

k

i

θ

j

i

θ

l

j

k,l

Впоследнее соотношение входит εikl – символ Леви-Чевита. Преобразования L, R оставляют инвариантной квадратичную

форму х у, определенную следующим образом

3
x y = x0 y0 − ∑ x j y j .	(1.56)

j=1

Эта форма известна как (псевдо) скалярное произведение в пространстве Минковского и может быть записана в терминах псевдо-

метрического тензора G с компонентами gμν :

	gμν = 0, μ ≠ ν; gμν =1,
μ = ν = 0, gμν = −1, μ = ν ≠ 0		(1.57)
x y = ∑ gμνxμ yν = ∑ gμνxμ yμ = xT Gy.
μν	ν

В последнем соотношении x, y – матрицы. Если Λ = LR для любых L, R то для каждой пары x, y

44

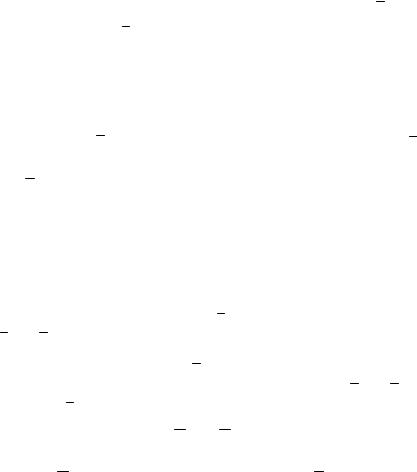
		(Λх)(Λу) = х у.							(1.58)
В терминах метрического тензора
						T GΛ = G .			(1.59)
				Λ
Очевидно, что		образуют группу: легко проверить, что
	Λ
					G			T = G .	(1.60)
			Λ				Λ

Вычислив определители в выражении (1.59), получим, (det Λ)2 =1, следовательно (det Λ) = ±1 .

Рассмотрим обращение пространственных координат в про-

странстве Минковского: (Is x)0 = x0 , (Is x)i = –xi . Очевидно,									что Is
входит в	Λ	и det Is = –1. Если det			Λ		= –1, то можно записать
				= Is (Is				).	(1.61)
			Λ				Λ

При это det (IsΛ) = +1. Если обозначить, через L+ подгруппу L , состоящую из матрицы с единичным определителем, то окажется, что L состоит либо из матриц L+, либо из произведений Is и матриц

L+.

Выберем единичный 4-вектор nt вдоль временной оси с компо-

нентами ntμ = δμ0.

Для заданного

из

мы можем иметь или

Λ

L

(

nt )0 > 0 или

(

nt )0 < 0 .

Невозможно иметь

(

nt )0 = 0 . Более

Λ

Λ

Λ

того, если (

n

)

> 0 и (

′n

)

> 0 , то (

−1n )

> 0 и (

′n )

> 0 .

Λ

0

Λ

0

Λ

ΛΛ

0

t

t

t

0

t

Таким образом, подмножество из L , состоящее из преобразований Λ с (Λnt )0 > 0 , образует группу, называемую ортохронной груп-

пой Лоренца и обозначаемой L↑. Соответствующие ей преобразо-
вания сохраняют направление времени. Если матрица Λ из L та-
кова, что (Λnt )0 < 0 , то можно записать
Λ = I (IΛ),	(1.62)

где I – полное обращение I = It Is: Ix = –x. Очевидно, что в этом случае (IΛnt )0 положительно. Любой элемент L является либо

элементом L↑, либо произведением IΛ c Λ L↑.

45

Наконец, собственная ортохронная группа L↑+ (которую обычно

называют просто группой Лоренца) – это группа матриц Λ, таких, что

ΛT GΛ = G, det Λ =1, Λ	00	> 0 .	(1.63)

Как было показано выше, любой элемент Λ из L имеет одну из форм

Is Λ, It Λ, IsIt Λ, Λ,

(1.64)

где Λ L↑+ .

Преобразования Is, It, I иногда называют несобственными

преобразованиями. Покажем, что если R L и Rnt = nt , то R – вращение.

Условие Rnt = nt подразумевает, что R имеет вид

1		0	0	0
	0		ˆ		(1.65)
R =	0			,
			R
	0

ˆ

R

T

GR = G дает

ˆT ˆ

где R – матрица 3×3. Условие

R R =1 , а условие

ˆ

ˆ

SO(3), т.е. являет-

det R = +1 означает, что det R = +1. Поэтому R

ся 3-мерным вращением. Пусть Λ произвольное вращение из L и

пусть u ≡ Λut . Тогда u0 > 0 и u u =1. Выберем вектор

ξ , такой,

G

G

что u0 = cosh

ξ

,

u

= sinh

ξ

. Это возможно, поскольку

1 = u u = (u0 )2 −

uG

2 = cosh2 ξ −sinh2 ξ.

(1.66)

G

Пусть ξ ориентирован вдоль n

nG

ξ

G

=

G

,

(1.67)

ξ

n

так что

u0 = cosh ξ,

ui

=

1 (sinh ξ) ξi .

(1.68)

2

46

Используя точные выражения для L (ξG) , получаем, L (ξ) nt = u .

Таким образом, преобразование L−1 (ξ)Λ , обладающее свойством

L−1 (ξ)Λnt = nt

(1.69)

должно быть вращением, характеризуемым некоторым θ.

Иначе говоря, любое ортохронное лоренцевское преобразование

Λ можно представить в виде	G
		(1.70)
Λ = L (ξ)R (θ),

где R – вращение, L – лоренцевский сдвиг (однако такое разложение – не единственное).

ГруппаG ЛоренцаG является 6-мерной группой Ли (три параметра

от θ и три от ξ ). Она очевидным образом некомпактна (параметры

G

ξ могут принимать произвольно большие значения), является про-

стой и дважды связанной группой. Ниже мы найдем её накрывающую группу, котораяG совпадает с SL(2,C). Заметим, что лоренцев-

ский сдвиг L (ξ) может быть записан в виде

R′L (ξz ) R′′,	(1.71)
где R′, R′′ = R′−1 – вращения и L (ξz )	– ускорение вдоль оси ОZ.

Таким образом, общие лоренцевские преобразования сводятся к вращениям и ускорениям, которые можно считать происходящими

вдоль оси OZ.
Вместо		G	параметризации		лоренцевского преобразования
	G			ξ и	θ часто используют ковариант-
Λ = L (ξ)R		(θ) параметрами
ную параметризацию. Определим набор параметров ωμν								в терми-
G	G
нах ξ	и θ:
			∑ε jklωjk = θl,	ωj0	=	1	ξ j, ωαβ = −ωβα .	(1.72)
			j,k		2

Тогда бесконечно малое преобразование Лоренца записывается в виде

47

Λ =1− ∑ωαβX (αβ) + O (ω2 ).	(1.73)
Матрицы X (αβ) имеют компоненты
X (αβ) = −(δμαgνβ − δμβgνα ) .	(1.74)

Чтобы доказать это утверждение, заметим, что с одной стороны, из определения Х, имеем

(Λ(ω) x)μ = xμ − ∑∑ωαβXμν(αβ)xν .						(1.75)
		α,β	ν
С другой стороны, с учетом точных формул для R, L:
(R (θ) x)		G			= xi − ∑2ωik xk ;
		= x0 ; (R (θ) x)		i		(1.76)
G		0			G
(L (ξ) x)0	= x0 + ∑2ωj 0 xj ;		(L (ξ) x)i = xi + 2ωi 0 x0			;

Поэтому, полагая Λ = LR, получим

(Λx)0 ≈ x0 −∑2ω0 j x j; (Λx)i ≈ xi + 2ω0ix0 −∑2ωik xk. . (1.77)

Откуда и следует ожидаемый результат (1.73), (1.74).

Помимо L↑+ , группа симметрии теории относительности вклю-

чает пространственные трансляции
r → rG + aG ,	(1.78)
и временные трансляции
ct → ct + a0.	(1.79)
В 4-векторных обозначениях
xμ → xμ + aμ.	(1.80)

Группа, получающаяся при объединении L и трансляций, называется группой Пуанкаре или неоднородной группой Лоренца, и обозначается обычно через L. Её элементы – пары (а, Λ) 4-векторов а и Λ L. Они действуют на произвольный вектор х следующим образом

(а, Λ)x = a + Λx

(1.81)

и удовлетворяют условиям

	(a, Λ)(a , Λ ) = (a + Λa , ΛΛ ),
	′	′	′ ′	(1.82)
	(a, Λ)−1	= (−Λ−1a, Λ−1 ).

Единичный элемент группы Пуанкаре – преобразование (0,1).

48

1.2.3. Геометрия пространства Минковского

Векторы v пространства Минковского можно релятивистки инвариантным образом разделить на следующие классы: времениподобные, светоподобные и пространственноподобные вектора. Времениподобные – это такие вектора, для которых v v > 0. Если v0 > 0, то о таких векторах говорят как о положительных времениподобных векторах; если v0 < 0 – отрицательных времениподобных

векторах (v0 = 0 – невозможно). Для светоподобных векторов v v = 0. Вектора называют положительными светоподобными, если v0 > 0 и отрицательными, если v0 < 0. Случай v0 = 0 возможен только для нулевого вектора v = 0. Наконец v – пространственноподобен, если v v < 0; знак в этом случае не является инвариантом. Если v – положительный (отрицательный) времениподобный вектор, то существует вектор v(0) и Лоренц преобразование Λ такое,

что v = Λv(0) и v0(0) = ±m, vG0 = 0, m > 0.

Если v – положительный (отрицательный) светоподобный вектор, то существует вектор v и преобразование Λ, для которых v = Λv и v0 = ±1, v1 = v2 = 0, v3 =1.

Если v – пространственноподобный вектор, то существует век-

тор	v(3)		и	преобразование Λ, для которых v = Λv(3) , причем
v(3) = δ			v(3), v(3) > 0 . Эти утверждения означают, что в некоторой
μ		μ3 3		3

системе отсчета положительный светоподобный вектор может быть выбран в виде

v = (1 0 0 1) . (1.83)

Отличие между евклидовым пространством и пространством Минковского проявляется в двух приведенных ниже утверждениях.

1. Если v и v′ светоподобны и ортогональны, т.е. v v′= 0, то они они параллельны: v′ = αv .

2. Если v v′≥ 0 и v u = 0, то либо v и u пропорциональны, либо u – пространственноподобный вектор.

49

Единственными инвариантными тензорами в пространстве Минковского являются комбинации метрического gμν и символа Леви-Чевита ε:

εμνρσ = 1, если μνρσ – четная перестановка 1230 εμνρσ = –1, если μνρσ – нечетная перестановка 1230 (1.84)

εμνρσ = 0, – если два индекса одинаковы.

Для заданного вектора v пространства Минковского набор лоренцевских преобразований Г, которые оставляют вектор неизменным, называется, как уже отмечалось, малой группой (или стабилизатором) W(v). Малая группа вектора v зависит только от знака v v в том смысле, что если v v > 0 и u u > 0, то малые группы W(v) и W(u) изоморфны. Чтобы доказать это утверждение, заметим, что W(v) и W(Λv) изоморфны для любого Λ. Действительно, если Гv = v, то ГvГ–1 принадлежит W(Λv) и наоборот. Более того, W(v) идентична с W(αv) для любого числа α ≠ 0. Таким образом, оказываются существенными только три малые группы. Точнее, если

v v > 0, малая группа изоморфна W(nt), если же v v = 0,			малая
группа изоморфна W (v ), v0 = v3,	v1 = v2 = 0 ; если v v < 0,		малая
группа изоморфна W(n(3)), n(3) = δ	μ3	. Это обстоятельство упрощает
μ
изучение малых групп.
Малая группа W(nt) = SO(3)	– группа 3-мерных вращений.
W (v) = SO(2) T2 , SO(2) – группа вращений вокруг оси OZ, а Т2
будет определена ниже.

W (n(3)) = Z+↑ (3) , где Z+↑ (3) – «лоренцеподобная» группа в 3-х

измерениях, действующая только на время и на плоскости XOY и оставляющая OZ неизменной. Первое из утверждений нам уже известно. Обратимся ко второму (светоподобному) случаю. Пусть Г – элемент W (v ) и N – подпространство пространства Минковского,

ортогональное к v , т.е. если u N, то u v = 0 . Очевидно,				что под-
пространство N инвариантно относительно Г. Базис N образуют три
вектора v(a),	a = 1, 2, 3 c v(1) = n(1), v(2) = n(2), n(a) = δ	aμ	и	v(3) = v .
	μ
Поскольку v	– светоподобный вектор, подпространство,			ортого-
	50