Емелянов Фундаменталные симметрии 2008

это увидеть, следует воспользоваться соотношениями (4.11), (4.9)

и (4.7) (1−δaiGi )χα (x)(1+ δaiGi ) = χα (x) +iδai (gi )αβ χβ.

(4.12)

Отсюда следует

α

(

x

)

= −

(

g

i )αβ

χ

β (

x

)

.

(4.13)

i

G ,χ

Это выражение определяет, как квантовые поля χα преобразуются относительно группы G. Подставив (4.13) в тождество Якоби

G , G	,χ		+ χ	G	,G	+ G ,	χ	α	,G	= 0, (4.14)
i j		α		α, i	j	j [			i ]

получим, что матрицы gi удовлетворяет соотношению (4.10). Обсудим более подробно свойства теории, включающей кванто-

вые поля χα , инвариантные относительно преобразований группы

G. Как будет видно, инвариантность относительно преобразований группы G подразумевает существование сохраняющихся токов. Поскольку плотность лагранжиана, вообще говоря, зависит от χα

и их пространственно-временных производных ∂μχα , то инвари-

антность действия (4.2) означает, что
∫d 4 xL (χα ,∂μχα ) = ∫d 4 xL(χ′α ,∂μχ′α ).	(4.15)

Для χ′α , которые получаются при инфинитезимальном преобразовании χα , условие стационарности действия дает

			∂L		∂L
	0	= δS = ∫d 4 x		δχα +		δ∂μχα	=
			∂χα		∂∂μχα

			4				∂L			∂L
	∫			∂L
=		d		x		− ∂μ			δχα + ∂μ		δχα
					∂χα		∂∂μχα			∂∂μχα

(4.16)

.

Первый член в фигурных скобках обращается в ноль вследствие уравнений движения Эйлера-Лагранжа. Второй член можно пере-

	писать в терминах матрицы gi. Поскольку
		δχα = χ′α − χα = −iδai (gi )αβ χβ ,									(4.17)
			∂L 1				(gi	)αβ
	то	0 = δS = −∫d 4 xδai∂μ							χα .		(4.18)
			∂∂μχα i

141

Так как параметры δаi – независимые, то ток
	Jiμ (x) =	∂L		1	(gi )	αβ χβ	(4.19)
		∂∂μχα i
сохраняется	∂μJiμ (x) = 0 .						(4.20)

Поскольку предполагается, что поля χα достаточно быстро

уменьшаются при стремлении к пространственной бесконечности, существует набор постоянных величин (обобщенных зарядов), задаваемых интегралами

	Qi = ∫d 3 xJi0 ;	d	Qi = 0.	(4.21)
		dt

Легко проверить, что операторы Qi совпадают с генераторами Gi. Они удовлетворяют соотношениям (4.10) и (4.13). Действительно, если Н – гамильтониан системы, то гейзенберговское уравнение движения подразумевает

	[H ,Gi ] = 0 .					(4.22)
	Проверим, что действительно
		∂L 1		(gi )αβ
	Gi ≡ Qi = ∫d 3xJi0 = ∫d 3x				χβ	(4.23)
		∂∂0χα i

действует как генератор. Для этого заметим, что канонический импульс, сопряженный с χα

	πα (x) =		∂L		.	(4.24)
		∂∂0	χα	(x)

Для бозонных полей канонические импульсы удовлетворяют одновременным коммутационным соотношениям

π

α (

x

)

,χ

β (

x

0

0

=

1

∂3

(

xG

− yG

)

δ

αβ

;

)

x

=y

i

(4.25)

πα (x),πβ (x)

= χα (x),χβ

(x)

= 0

x0 =y0

x0

=y0

Тогда

Gi

≡ ∫d

3

πα (x)

1

(gi )αβ

.

(4.26)

x

i

χβ

142

Так как Gi не зависят от времени, то при вычислении коммутатора

Gi с χγ ( y)

можно положить в выражении (4.26)

x0 = y0 . С помо-

щью (4.25) имеем

1

(gi )αβ

G ,χ

γ (

∫

3 x

πα (x)

×

(

i )

β (

)

. (4.27)

y

=

d

i

= −

g

γβ

χ

y

i

)

×χβ (x),χγ ( y)

0

0

При этом

x

=y

πα

(x)

1

(gi )αβ χβ (x),

3

3

i

= ∫ d xd y

=

Gi ,G j

1

πγ ( y)

(g j )γδ χδ ( y)

0

0

i

x

=y

d 3 xπ

x

1

g

, g

χ

x

=

(4.28)

∫

α

(

)

β

(

)

i

j

i

αβ

= iCijk ∫ d 3xπα (x)(gk )αβ χβ (x) = iCijk Gk ,

что и требовалось показать.

До сих пор при обсуждении симметрий мы фокусировались на трансформационных свойствах квантовых полей χα (x) . Соответствие между квантовыми полями и частицами предполагает, что квантовые состояния, ассоциированные с полями χα (x) , будут преобразовываться аналогичным образом. Обозначим одночастичное состояние, связанное с полем χα , через p;α , где pμ – 4-х им-

пульс этого состояния, причем p2 = mα2 . Тогда из (4.7) следует

U −1(a)		p;α = R (a)		p;β .	(4.29)
		αβ

Это соотношение можно использовать для нахождения всех со-

стояний мультиплета		p;α , имеющих ту же массу. Пусть						p;α rest
обозначает состояние с 4-х импульсом pμ = (0,mα ). Тогда, по оп-
ределению, действие гамильтониана на это состояние дает
H				p;α rest = mα		p;α rest .	(4.30)
143

Однако, если теория инвариантна относительно группы G, т.е. Н коммутирует со всеми ее генераторами, то

H ,U −1(a)

= 0 .

(4.31)

Применяя это соотношение к «rest» состоянию, получаем

0

= H ,U

−1 (a)

p;α

= HU −1

(a) −U −1 (a)H

p;α

=

rest

rest

(4.32)

= Rαβ (a)(mβ − mα )

p;β rest .

Поскольку

Rαβ (a) – произвольна, то действительно получаем для

мультиплета mα = mβ .

Говорят, что симметрия реализована Вигнер-Вейлевским образом, если инвариантность действия относительно группы G приводит к появлению в природе мультиплетов частиц одинаковой массы. Хорошо известный пример (приближенной) вигнервейлевской симметрии – сильный изоспин. Приближенная глобальная SU(2) симметрия сильных взаимодействий приводит к вы-

рожденности нуклонного дублета (mp = mn ) и пионного триплета

(mπ+ ≈ mπ− ≈ mπ0 ) . Однако вигнер-вейлевский способ – не единственный способ реализации симметрии.

4.2. Намбу – голдстоуновская реализация симметрии

Оказывается, возможен случай, когда действие инвариантно относительно группы симметрии G, а физические состояния теории не обладают этой симметрией. Этот происходит в случае, когда

H ,U −1	(a)	= 0 ,	(4.33)

однако вакуумное состояние не инвариантно относительно группы G. Такие симметрии называются спонтанно нарушенными или реализованными намбу-голдстоуновским образом. Соотношение

(4.29), из которого следует, что все состояния мультиплета p;α

вырождены по массе, получено из трансформационных свойств квантовых полей χα в предположении о том, что вакуумное состояние инвариантно относительно группы G

144

U (a)		0 = 0 .	(4.34)

Одночастичные состояния p;α могут быть построены действием (асимптотических) операторов рождения на поле χα . Для скалярного поля

χα (x) = ∫

d 3 p

eipxaα ( p,t)

+

(

.

(4.35)

(2π)

3

2 p

α

p,t

)

0 +e−ipxa+

Тогда

1

p,α = lim

a+

(

p,t

)

0

=

lim

d 3 peipx

∂

χ

(

x

)

0 ,

(4.36)

x→±∞

α

x→±∞ ∫

i

0

α

←→

где

A

∂

0 B = A∂0 B −(∂0 A)B .

(4.37)

Рассмотрим, как и в соотношении (4.29),

действие U −1 (a)

на со-

стояние

p;α

U −1 (a)

p;α =

lim aα+ ( p,t)

0

=

x0

→±∞

(4.38)

= lim

∫

d 3 peipx

1

∂ U −1

(

a

)

χ

α (

x

)

0 .

x→±∞

i

0

Если условие (4.34) выполнено, то можно записать

U −1 (a)χα (x)

0 =U −1 (a)χα (x)U (a)

0 =

(4.39)

= Rαβ (a)χβ (x)

0 ,

откуда следует выражение (4.29). Однако, если вакуум неинвариантен по отношению к преобразованиям группы G, т.е. если вакуумное состояние вырождено или неединственное, то, несмотря на то, что поля χα преобразуются по неприводимому представлению

группы G, вырожденные мультиплеты в спектре отсутствуют. Если симметрия реализована намбу-голдстоуновским образом,

то вместо мультиплетов частиц одинаковых масс в теории возникают безмассовые возбуждения – бозоны Намбу-Голдстоуна. Чтобы это увидеть, найдем вакуумное среднее от (4.13)

	i	α (		)		(		i )αβ			β (		)
0	G ,χ		x		0 = −		g		0	χ		x		0 .	(4.40)
					145

Если вакуум инвариантен относительно преобразований группы G, то

Gi		0 = 0 .	(4.41)

Из соотношения (4.40) следует, что вакуумные средние полей χα равны нулю. Если же соотношение (4.41) не выполняется и χα – скалярные поля, то ничто не противоречит предположению

0		χα (x)		0 ≠ 0 .	(4.42)

Если χα описывают поля со спином, отличным от нуля, то ана-

лог соотношения (4.40), наряду с инвариантностью вакуума относительно этих преобразований, приводит к нулевым значениям вакуумных средних этих полей.

Симметрия реализуется намбу-годстоуновским образом, если существует некоторое скалярное поле (не обязательно элементарное) с ненулевым вакуумным средним. Предположим, что это имеет место для соотношения (4.40). Тогда, используя определение (4.23) генераторов Gi , получим

0 ≠ −(gi )αβ 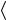0 χβ (x) 0 = (4.43)

= ∫d 3 y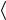0 Ji0χα (x) − χα (x) Ji0 ( y) 0.

Это соотношение можно записать по другому, вставляя полный набор состояний n и используя трансляционную инвариантность токов

Ji0 ( y) = e−ipy Ji0 (0)eipy .

(4.44)

Тогда правая часть (4.43) запишется в виде

∑ ∫ d3 y{

0

e−ipy Ji0eipy

n n

χα (x)

0 − 0

χα (x)

n n

e−ipy Ji0eipy

0 } =

n

= ∑ ∫ −d3 yeipn y 0

Ji0 (0)

χα (x)

n n

0 −

(4.45)

n

−∑ ∫ d3 ye−ipn y 0

χα (x)

n n

Ji0 (0)

0 = ∑ (2π)3 δ3 ( pGn )×

n

n

×{e−ipn0 y0 0

Ji0 (0)

n n

χα (x)

0 −eipn y 0

χα (x)

n n

Ji0 (0)

0

}.

146

По предположению, это выражение не обращается в ноль. Более того, поскольку левая часть (4.43) не зависит от y0 , то и (4.45) не зависит от y0. Очевидно, что это возможно, если в теории существуют некоторые безмассовые одночастичные состояния n , имен-

но они вносят вклад в сумму (4.45). Эти безмассовые состояния называются голдстоуновскими бозонами.

Нетрудно убедиться, что каждый генератор Gi , который не аннигилирует вакуум, связан с годстоуновским бозоном (при действии Gi на вакуум возникает некоторое состояние, и это сотояние ассоциируется с годстоуновским бозоном). Представим состояние голдстоуновского бозона как p; j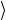 , причем p2 = 0 . Тогда матрич-

ные элементы токов, связанных с нарушенными генераторами, отличны от нуля

0		Jiμ (0)		p; j = if jδij pμ ,	(4.46)

где f j – некоторые отличные от нуля константы, зависящие от ва-

куумных средних полей χα . Действительно, если вспомнить, что для одночастичного состояния

∑ ≡

d 3 pn

,

(4.47)

∫ (2π)3

2 pn0

n

то из соотношений (4.43) и (4.45) имеем

i(gi )

χβ (0)

1

fi

p;i

χα (0)

0 +

0

0 =

lim

.

(4.48)

αβ

p

μ

→0

2

+ fi

*

0

χα (0)

p;i

Проиллюстрируем намбу-голдстоуновскую реализацию простым примером. Рассмотрим случай комплексного скалярного поля ϕ с плотностью лагранжиана

	+			+		1		2
L = −∂μφ		∂μφ − λ	φ		φ −		f	.	(4.49)
						2

Очевидно, что теория инвариантна относительно U(1) преобразований

147

φ(x) → φ′(x) = eiαφ(x)

(4.50)

φ+ (x) → φ′+ (x) = e−iαφ+ (x).

Сохраняющиеся токи, связанные с этой симметрией, строятся с помощью соотношения (4.18)

∂L 1

∂L

1

J μ =

φ +

(−1)φ+ = i((∂μφ)φ −(∂μφ)φ+ ).

(4.51)

∂∂μφ

i

∂∂μφ+

i

Соответствующий генератор

(∂0φ+ )φ −

G = ∫d 3xJ 0

= i∫d 3x

−(∂

0

φ)φ

+

(4.52)

удовлетворяет коммутационным соотношениям

[G,φ( x)] = −φ( x)

(4.53)

G,φ+ ( x) = φ+ ( x).

В классическом смысле, второй член в лагранжиане (4.49) соответствует потенциалу полей ϕ и ϕ+

	V (φ,φ+ ) = λ	φ+φ −	1	f	2 .	(4.54)
			2
	Чтобы гарантировать положительность			теории, следует		считать

λ > 0. Физика теории зависит от знака f. Если f < 0, то мы имеем единственный минимум при ϕ = ϕ+ = 0, и симметрия теории реализована Вигнер-Вейлевским способом, приводящим к вырожденному мультиплету массивных состояний. Если же f > 0, то потенциал имеет бесконечное число минимумов, определяемых условием

φφ+ = f 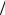2 . В этом случае симметрия реализована намбу-

голдстоуновским образом, и в теории имеются как массивные, так и безмассовые состояния. Если f < 0, разложим потенциал вблизи минимума

V (φ,φ

+

) = λ

+

1

2

1

2

+

φ + λ(φ

+

φ)

2

.

(4.55)

φ

φ −

f

=

λf

− λf φ

2

4

Квадратичный член

−λ f φ+φ

при f < 0 массовый член полей

ϕ и ϕ+:

148

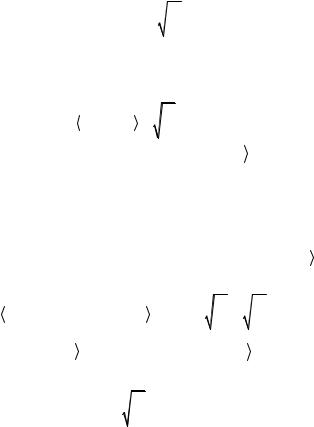
mφ2 = mφ2+ = −λf > 0 .

(4.56)

В этом случае имеется вырожденный мультиплет из двух зарядовосопряженных частиц, взаимодействующих посредством λ(φ+φ)2

члена.

Если же f > 0, то разложение вблизи ϕ = 0 теряет смысл, поскольку потенциал имеет локальный максимум. Разумно разложить

	потенциал вблизи минимума φmin =	f	eiθ . Так как f > 0, то квад-
		2

ратичный член φ+φ уже не определяет массу.

С точки зрения квантовой механики, ненулевое значение ϕmin подразумевает, что ϕ имеет ненулевое вакуумное среднее

0		φ( x)		0 =	f	eiθ .	(4.57)
					2
Фаза θ, характеризующая вакуумное состояние								θ , на самом деле,

несущественна, и её можно вращением исключить. Это следствие неединственности вакуума теории. Так как при U(1) преобразованиях

U −1 (α)φ( x)U (α) = eiαφ( x) ,

(4.58)

то очевидно, что среднее ϕ(х) между состояниями U (−θ)

θ

– ве-

щественно. Действительно,

θ

U −1 (θ)φ( x)U (−θ)

θ = e−iθeiθ

f

=

f

.

(4.59)

Очевидно, что U (−θ)

2

2

θ такой же вакуум, как и

θ .

Положим θ = 0 и разложим ϕ в виде

φ =

f

+ χ ,

(4.60)

2

где квантовое поле χ, по предположению, имеет нулевое вакуумное среднее. Потенциал в терминах поля χ запишется в виде

149

+

+

1

2

+

f

+

2

V (φ,φ

) = λ

φ

φ −

f

= λ

χ

χ +

(χ + χ

)

=

2

2

(4.61)

= λ2f (χ + χ+ )2 + 2 f χ+χ(χ + χ+ ) + λ2 (χ+χ)2 .

Очевидно, что линейная комбинация полей χ и χ+ имеет массу, а ортогональная комбинация к ней – безмассовая. Обозначим

χ+	=	1	(χ + χ+ );	χ− =	i		(χ+	− χ) .	(4.62)
		2
				2
Тогда			m+2 = 2λf ;	m−2 = 0 .					(4.63)
Несмотря на то,	что лагранжиан (4.49)					U(1)		– симметричен, эта

симметрия отсутствует в спектре! Идентификация χ− как голдсто-

уновского бозона следует из коммутаторов (4.53). Так как f вещественна, то

χ− =

i

(χ+ − χ)

=

i

(φ+ − φ) .

(4.64)

2

2

Следовательно,

i

(φ+ + φ) = i( f + χ+ ) .

[G,χ− ] =

(4.65)

2

Найдем вакуумное среднее

0

[G,χ− ]

0

= i

f .

(4.66)

Из этого соотношения следует, что χ−

– голдстоуновский бозон.

Если p – состояние голдстоуновского бозона, то, пренебрегая

нелинейностью, можно ожидать, что
0				χ− (0)				p	=1 .	(4.67)
Тогда из (4.66) имеем
0		J μ (0)				p = i			f pμ .	(4.68)
Константа распада fi в (4.46) здесь представляет собой										f и свя-

зана с вакуумным средним поля ϕ соотношением (4.48). Есть и другой способ индентификации этих констант, если исходить из

150