Емелянов Фундаменталные симметрии 2008

конечных факторизованных VEV с nμi = nμ f i . Для этих целей обобщим выражение (1.229) на конечное преобразование

aμα = exp[(ωα)]aμαexp[−(ωα)] .

(1.241)

Таким образом, калибровочно-инвариантные абелевы и неабелевы теории могут быть получены, исходя из требования физической ненаблюдаемости СНЛС.

1.4. Конформная симметрия

Среди общих координатных преобразований 4-мерного пространства Минковского, сохраняющих интервал ds2 = = gμν (x)dxμdxν , имеются такие преобразования, которые изменяют только масштаб метрики:

′ ′	) = gw(x) gμν (x)	(1.242)
gμν (x

и, следовательно, оставляют углы на световом конусе инвариантными. Такого типа преобразования относятся к конформной группе. Очевидно, что конформные преобразования соответствуют обобщенной группе Пуанкаре, поскольку метрика Минковского не меняется при трансляциях и лоренцевских вращениях. Примерами конформных преобразований могут служить дилатации (глобальные преобразования метрики) и инверсия:

xμ → x′μ = λxμ; xμ = x′μ =	xμ	(1.243)
	x2

с вещественными λ. Другой важный пример – специальное конформное преобразование

xμ → x′μ =	xμ + aμx2
	1+ 2a x + q2 x2 ,	(1.244)

которое соответствует инверсии, трансляции на произвольный постоянный вектор аμ и еще одной инверсии относительно того же центра.

Конформная алгебра в 4-х измерениях содержит 15 генераторов

81

	Pμ	(4 трансляции)
	Mμν	(6 лоренцевских вращений)	(1.245)
	D	(дилатация)
	Kμ	(4 специальных конформных преобразования)

и обобщение известной 10-параметрической алгебры Ли группы Пуанкаре, генерируемой Pμ и Mμν :

i P , P

= 0,

i M

aβ

, P

= g

P − g

P ;

(1.246)

μ ν

μ

αμ β

βμ α

i M

αβ

, M

= g

αμ

M

βν

− g

βμ

M

αν

−

μν

(1.247)

−gανMβμ + gβνMαμ.

Оставшиеся коммутационные соотношения, определяющие конформную алгебру

i D, P

= P ,i D, K

= K

μ

;

μ

μ

μ

i P , K

= −2g

μν

+ 2M

μν

;

μ

ν

i M	αβ	,

i D, M

K

= g

αμ

K

β

− g

βμ

K

α

;

μ

(1.248)

= i K

, K

= 0.

μ

μν

ν

Генераторы действуют на фундаментальное поле Φ(x) вольного спина следующим образом

δμΦ(x) ≡ i

Pμ,Φ(x) = ∂μΦ(x);

M

P

(

)

xμ∂ν − xν∂μ −Σμν

δμνΦ(x) ≡ i M μν,Φ(x)

=

Φ(x);

K

δDΦ(x) ≡ i[D,Φ(x)] = (x ∂ +l)Φ(x);

ν

)

(

δμ

Φ(x) ≡ i Kμ,Φ(x)

==

2xμx ∂ − x2∂μ + 2lxμ − 2x

Σμν

Φ(x).

произ-

(1.249)

Например, если рассматриваются бесконечно малые трансляции xμ → xμ′ = xμ + εμ , то поле Ф преобразуется следующим образом

′		μ			(1.250)
Φ	(x) = 1	+ εμδP Φ(x)
Σμν – генератор спиновых вращений поля					Φ(x). Для скаляров,
дираковских спиноров (кварков) и векторных (глюонных) полей
Σμνϕ(x) = 0, Σμνψ =			i	σμνψ;
		2			(1.251)

Σμν Aα = gνα Aμ − gμα Aν,

82

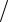
где	σμν = i γμ,γν		2 .

Параметр l называется масштабной размерностью, этот параметр определяет изменение поля при дилатациях. В свободной теории (на классическом уровне) масштабная размерность совпадает с

канонической размерностью (lcan ) , которая фиксируется требова-

нием безразмерности действия. В квантовой теории l ≠ lcan , и их размерность называется аномальной размерностью. Для ультрарелятивистской частицы (кварка или глюона), распространяющейся вблизи поверхности светового конуса, оказывается существенным разделение продольных и поперечных координат. Удобно ввести следующие обозначения для проекций на два независимых светоподобных вектора. Для произвольного 4-вектора Aμ определим

величины

A	≡ A nμ,	A	≡ A nμ, n2	= n 2 = 0, n n =1	(1.252)
+	μ	−	μ

и метрический тензор в направлениях, ортогональных к световому конусу

g	= g	μν	− n n	− n n .	(1.253)
μν			μ ν	ν μ

Будем использовать также обозначение A для поперечной проек-

ции и Aμ для вектора, имеющего только поперечные компоненты. Например,

xμ = x	−	nμ + x nμ + xμ		;	xμ	≡ gμνx .	(1.254)
		+				ν

При этом x2 = 2x+x− − x2 .

Рассмотрим случай конформных преобразований (1.244), для которых aμ – светоподобный вектор aμ = anμ . Тогда

x	→ x′	=			x−	.	(1.255)
			1
−	−				+ 2ax
					−

Эти преобразования отображают световой луч в х-направлении на самого себя. Совместно с трансляциями и дилатациями в этом направлении x− → x− + c и x− → λx− , эти преобразования составляют

коллинеарную подгруппу полной конформной группы. Эта под-

83

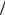
группа – SL(2,R), и именно она играет центральную роль в последующем анализе.

В партонной модели адронные состояния заменяются пучком коллинеарных партонов, движущихся в том же направлении, скажем, nμ . Вне зависимости от конкретной модели, необходимо

лишь считать, что кантовые поля «живут» на световом луче
Φ(x) → Φ(αn) ,	(1.256)

где α – вещественное число.

Для упрощения обозначений часто считают, что Φ(x) ≡ Φ(αn) . Предположим, что поле Ф является собственным состоянием оператора спина Σ+− и имеет фиксированную проекцию s на (+) на-

правление:
Σ+−Φ(α) = sΦ(α) .	(1.257)

В общем случае для разделения различных спиновых компонент необходимо использовать соответствующие проекционные операторы. Примеры будут обсуждаться ниже.

С учетом этих определений и обозначений, 4-мерные конформные преобразования сводятся к коллинеарной подгруппе, генерирующей проективные преобразования на линии

	α → α′ =	aα +b	, ad −bc =1,
		cα + d						(1.258)
					aα +b
	Φ(α) → Φ′(α) = (cα + d )			−2 j
					Φ			,
					cα + d

где a, b, c, d – вещественные числа, причем

j = (l + s) 2 .

(1.259)

Эти преобразования осуществляются четырьмя генераторами Р+, М+–, D и K, образующими коллинеарную подалгебру конформной алгебры (1.247, 1.248). Величина j называется конформным спином. Чтобы привести коммутационные соотношения к стандартному виду, удобно построить следующие линейные комбинации:

L = L +iL = −iP ;

L = L −iL =

i

K

−

;

+

1

2

+

−

1

2

2

(1.260)

i

(D + M

);

i

(D − M

).

L =

+−

E =

+−

0

2

2

84

Тогда	[L0 , L±] = ±L±;[L−, L+] = −2L0 ,	(1.261)
это алгебра группы SL(2,R), изоморфная O(2,1).

Действие генераторов (1.260) на квантовые поля можно вывести из соотношений (1.247):

		[L+,Φ(α)] = −∂αΦα ≡ L+Φ(α);
		[L−,Φ(α)] = (α2∂α + 2 jα)Φα ≡ L−Φ(α);	(1.262)
	d	[L0 ,Φ(α)] = (α∂α + j)Φα ≡ L0Φ(α),
где ∂α =		.
	dα

Генератор Е характеризует твист t = 12 (l − s) поля Ф:

	[E,Φ(α)] =	1	(l − s)Φ(α) .	(1.263)
		2

Генератор Е коммутирует со всеми Li . Определение (1.263) соот-

ветствует так называемому коллинеарному твисту (размерность минус проекция спина на плюс-направление). Его следует отличать от геометрического твиста (размерность минус спин), который относится к полной конформной группе.

Локальный полевой оператор Ф(α), определяющий проекцию спина (1.257), является собственным состоянием квадратичного оператора Казимира

	∑ [Li ,[Li ,Φ(α)]]j ( j −1)Φ(α) = L2Φ(α) ,							(1.264)
	i=0,1,2
где	L2 = L2	+ L2	+ L2	;	L2	, L	= 0	(1.265)
	0	1	2			i

и операторы Li удовлетворяют SL(2,R) коммутационным соотношениям

L , L		= L ;	L , L	= −2L .	(1.266)
0	±		− +	0

Из соотношений (1.258) и (1.264) следует, что поле Ф(α) реализует представление группы SL(2,R), определяемое параметром j, которое, как уже отмечалось, называется конформным спином поля.

85

Как видно из соотношения (1.259), величина j положительна, причем j принимает (полу)целые значения.

Помимо коллинеарной подгруппы, можно рассмотреть другую подгруппу, соответствующую преобразованиям двумерной попе-

речной плоскости xμ = (0, x1, x2 ,0) , определенным соотношениями

(1.254). Эта «поперечная» подгруппа содержит шесть генераторов Pμ , M μν , D и K μν и изоморфна SL(2,C).

Введём комплексные координаты

z = x	+ix ,	z = x −ix	2	= z* ,	(1.267)
1	2	1

в терминах в которых групповые преобразования выглядят следующим образом

z →	az + b	, z →		a	z +	b		,	(1.268)
	cz + d
			cz + d

где a, b, c, d – комплексные числа и ad −bc =1. Для фундаментальных полей, «живущих» в поперечной плоскости Φ = Φ(z, z ) , закон

преобразования

Φ(z, z ) → Φ′(z, z ) =

(1.269)

az + b

az +

b

= (cz + d )−2h (

c

z + d )−2h Φ

,

,

cz + d

c

z + d

где h = (l + λ)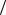2 , h = (l −λ)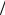2 и λ – спиральность поля, определяе-

мая как Σzz Φ = λΦ . Заметим, что коллинеарная и поперечная подгруппы имеют общий генератор дилатаций D, следовательно, они не являются независимыми.

Продолжим обсуждение конформной симметрии с простейшего примера – скалярного поля, описываемого действием

S [φ] =

∫

D

1

μ

2

2

d

x

∂

φ∂μφ− m

φ

−V (φ) .

(1.270)

2

В естественных единицах (h = c =1)

действие S [φ]

– безразмерно.

Тогда масса m должна иметь, как и производные ∂μ , размерность

(длина)−1 . Действие (1.270) инвариантно относительно преобразований группы Пуанкаре, т.е. относительно пространственных

86

трансляций, вращений и лоренцевских сдвигов. Симметрия относительно этих преобразований приводит к важным следствиям.

Рассмотрим влияние трансляционной инвариантности на функции Грина:

G(x1, x2 ,..., xn ) =	1	∫	Dφφ(x1)...φn (x)eiS[φ],
	Z
φ(xμ ) = φ′(xμ + aμ ), S [φ] = S [φ′].				(1.271)

Мера в выражении (1.271) тоже инвариантна относительно трансляций:

Πxdφ(x) = Πx−adφ(x − a) = Πx−adφ′ = Πxdφ′(x).

(1.272)

Следовательно,

G(x1,..., xn ) =

= Z1 ∫Dφ′φ′(x1 + a)...φ′(xn + a)eiS[φ′] = G(x1 + a,..., xn + a). (1.273)

Таким образом, функции Грина трансляционно-инвариантны, т.е. они могут зависеть лишь от разности их аргументов. Аналогичным образом, из лоренцевской (вращательной) инвариантности следует, что функции Грина могут зависеть от величин типа

(x1 − x2 )μ (x1 − x2 )μ ; (x1 − x2 )μ (x1 − x3 )μ и т. д.

Если в действии (1.270) положить m = 0 , то, в зависимости от конкретного выбора потенциала V (φ) , могут возникать «специаль-

ные» симметрии.

Обратимся снова к размерностям различных членов в действии. Пусть поля φ имеют размерности (длина)A . Это означает, что ки-

нетическая часть действия имеет размерность (длина)2 A−2+D . Тогда мы имеем произведение двух полей, дающее размерность (длина)2 A , двух производных с размерностью (длина)−2 и инте-

грал ∫d D x с размерностью (длина)D . Поскольку действие безраз-

	мерно, то следует положить A =	2 − D	. Потенциальный член в
		2
	87

(1.270) тоже должен быть безразмерным. Если считать, что V (φ) = gφP с безразмерной константой связи g, то возникает раз-

мерность (длина)P2 (2−D) . С учетом интегрирования ∫d D x , потен-

циальная часть действия имеет размерность (длина)P2 (2−D)+D . По-

этому следует положить P = (D2−D2) . Для D = 4 получаем

V (φ) = gφ4 , а при D = 3 V (φ) = gφ6 .

«Специальная» симметрия, о которой упоминалось выше, – это симметрия действия относительно масштабных преобразований

x′μ = λxμ . При таких преобразованиях безразмерное действие изменяется следующим образом:

1

2D

S [φ] = ∫d D x

∂μφ∂μφ− gφD−2 (x)

=

2

2D

(1.274)

−D

∫d

D

2 1

μ

x′

x′

x′ D−2

= λ

x′

λ

∂

φ

∂′μφ

− gφ

,

2

λ

λ

λ

где ∂′

=

∂

. Тогда

λ∂xμ

μ

= ∫d

D

1

μ

−(D−2)

x′

−(D−2)

x′

S[φ]

x′

∂′

λ

2 φ

∂′μ λ

2 φ

−

2

λ

λ

−(D−2)

2D

(1.275)

x′ D−2

−g λ

2 φ

.

λ

Если считать, что поля при масштабных преобразованиях изме-

′	(x) = λ	−	(D−2)		x′
			2
няются по закону φ				φ			, то действие окажется инва-
				λ

риантным относительно этих преобразований:

88

S[φ] = ∫dD x 1 ∂μφ(x)∂μφ(x) −gφ(x)							2D		=
							D−2
		2
= S[φ′] = ∫d	D			1		μ			2D		(1.276)
		x				∂ φ′(x)∂μφ′(x)−gφ′(x)D−2 .
				2

Но для масштабных преобразований мера оказывается неинвариантной

				D−2			D−2
∫	Dφ = ∏	∫	dφ(xi ) = ∏λ	2	∫	dφ′(xi′) =	∏λ 2	∫	Dφ′ .	(1.277)
	x		x				x
	i		i				i

Однако в определение функций Грина входит фактор Z1 . При этом

функционал Z приобретает такой же фактор, и эти факторы в числителе и знаменателе (1.271) сокращают друг друга. В результате вид 2-точечной функции Грина оказывается фиксированным:

	G(x1			− x2 ) =		1	∫	D−2	φ′(λx1)φ′(λx2 )eiS[φ′(x′)] =
								Dφλ 2
						Z
		1
	= λD−2			∫	Dφφ′(λx1)φ′(λx2 )eiS[φ′(x′)] = λD−2G(λ(x1 − x2 )). (1.278)
		Z

Из последнего соотношения следует, что 2-точечная функция Грина

G(x1 − x2 ) ~		1
			x − x	2		D−2	.	(1.279)
			1

Этот результат справедлив как для евклидова пространства, так и для пространства Минковского. До сих пор масштабные преобразования и пуанкаре-преобразования рассматривались отдельно. Комбинацию преобразований Пуанкаре и масштабных преобразований называют конформными преобразованиями. Отметим, что конформные преобразования сохраняют углы между векторами в D-мерном пространстве. Если говорить о пространстве Минковского, то надо иметь в виду, что конформные преобразования сохраняют углы в (3 +1) измерениях, а не в 3-х пространственных изме-

89

рениях. Более формально конформные преобразования можно определить как преобразования, которые не меняют отношения

dxα			dy
					α
	dx				dy			(1.280)
							.

Очевидно, что вращения, трансляции, лоренцевские сдвиги удовле-

творяют этому требованию.
При инфинитезимальном					координатном		преобразовании
x → x′ = x + ε(x)		метрический тензор в первом порядке по ε(x)
изменяется следующим образом
′	∂x′α ∂x′β			α	α	β	β
			= gαβ	(δμ	+∂με (x))(δν +∂νε (x)) =
gμν = gαβ		∂xμ ∂xν
								(1.281)
		= gμν + gμβ∂νεβ (x) + gαν∂μεα (x).

Если считать, что gμν → gμν′ = gμν (1+ Λ(x)) , то метрика просто домножается в каждой пространственно-временной точке x на число, т. е. такое преобразование является локально конформным преобразованием. Попытаемся найти функцию ε(x) , которая приводит

к такому преобразованию метрики. Сначала будем считать метрику плоской: gμν = ημν . Мы хотели бы получить

∂νεμ (x) + ∂μεν (x) = Λ(x)ημν .

Свертка этого уравнения дает

2∂μεμ (x) = DΛ(x),

где D – число пространственно-временных измерений. Тогда

∂νεμ (x) + ∂μεν (x) = 2 ∂k εk (x)ημν .

Dμ

Дифференцируя по ∂μ , имеем

	μ	2			∂ν (∂	μ	εμ (x)).
∂		∂μεν (x) =		−1
		D

Аналогично дифференцируя по ∂ν , получаем

90

(1.282)

(1.283)

(1.284)

(1.285)