metritchni_proct

p

≤(x1 − x3)2 + 2 cos ϕ(x1 − x3)(y1 − y3) + (y1 − y3)2 +

p

+ (x3 − x2)2 + 2 cos ϕ(x3 − x2)(y3 − y2) + (y3 − y2)2 =

= d((x1, y1), (x3, y3)) + d((x3, y3), (x2, y2)).

Таким чином, задана функцiя задовольняє всi три аксiоми вiдстанi, тобто надiляє множину R2 метрикою. ♦ Якщо на координатнiй площинi обрати декартову систему координат з кутом ϕ мiж осями координат (афiнний репер складається з одиничних векторiв з кутом ϕ мiж ними) i на нiй

взяти двi точки M1(x1, y1) i M2(x2, y2) (pис. 1),

Рис. 1

то з трикутника AM1M2 за теоремою косинусiв маємо

q

d(M1, M2) = AM12 + AM22 − 2AM1 · AM2 cos(π − ϕ) =

11

p

(x2 − x1)2 + (y2 − y1)2 + 2(x2 − x1)(y2 − y1) cos ϕ.

Такий же результат дiстанемо i при iнших розташуваннях точок M1 i M2 вiдносно осей координат.

Звичайно у множинi R2 можна задати метрику, яка не збiгається з евклiдовою. Наприклад, легко переконатись, що функцiя

d : R2 × R2 −→ R,

де для будь-якого елемента ((x1, y1), (x2, y2)) R2 × R2

d((x1, y1), (x2, y2)) = |x1 − x2| + |y1 − y2|,

надiляє множину R2 метрикою, яка очевидно не збiгається з евклiдовою.

Зауважимо також, що будь-яку непорожню множину можна надiлити так званою тривiальною метрикою

d(x, y) =	1,	якщо	x 6= y.
	0,	якщо	x = y,

Однак теорiя метричних просторiв з такою метрикою (простiр

здискретною метрикою) занадто "убога", щоб бути предметом вивчення.

Як правило, метрика у конкретнiй множинi є ефективним iнструментом дослiдження у тому випадку, коли вона пов’язана

зприродою елементiв цiєї множини та орiєнтується на задачi, якi виникають при такому дослiдженнi.

Крiм числових множин (множини, елементами яких є або дiйснi, або комплекснi числа) в аналiзi об’єктами дослiдження є множини, елементами яких є n-ки чисел або ж функцiї, зокрема послiдовностi. Не можна обминути множин, елементами яких є матрицi. Але перед тим, як перейти до розгляду конкретних метричних просторiв, розглянемо ряд нерiвностей, якi знадобляться у подальшому.

12

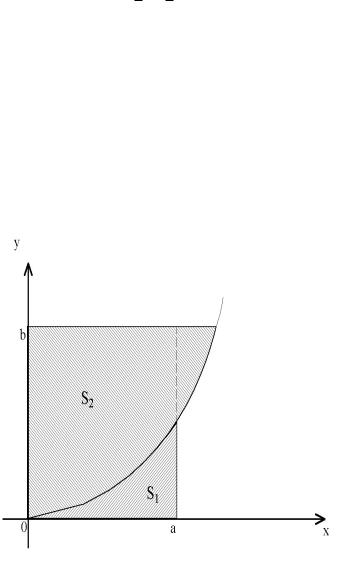
1. Нерiвнiсть Юнга. Якщо a ≥ 0, b ≥ 0, p > 1, q > 1 i

p1 + 1q = 1,

то

ab ≤	ap		bq		(1.2)
		+		.
	p		q

Доведення. Якщо або a = 0, або b = 0, то нерiвнiсть (1.2) очевидна. Оскiльки за умовою p > 1, то функцiя y = xp−1 зростаюча i неперервна на промiжку [0; +∞), а отже,i обернена до неї теж зростаюча i неперервна на промiжку [0; +∞). Вiзьмемо два додатних числа a i b i розглянемо площi криволiнiйних трапецiй (pис. 2):

Pис. 2

13

перша обмежена вiссю Ox, прямою x = a i кривою y = xp−1, а друга – вiссю Oy, прямою y = b i кривою x = yq−1 (q = p −p 1, q−

1

1 = p − 1). Очевидно, що якщо S1 i S2 площi вiдповiдно першої i другої криволiнiйних трапецiй, то

	a			b
ab ≤ S1 + S2 = Z		xp−1dx + Z yq−1dy =			ap		bq
						+		,
					p		q
	0	0
i нерiвнiсть (1.2) доведена.								♦
2. Нерiвнiсть Гельдера. Якщо p > 1, q > 1 i 1/p+ 1/q = 1,
то для будь-яких xi, yi R (i =				) виконується нерiвнiсть
			1, n
n	n			n		(1.3)
i=1 |xiyi| ≤	i=1	|xi|p 1/p i=1 |yi|q 1/q
X	X			X

Доведення. Нерiвнiсть очевидна, якщо або всi xi = 0 (i =

1, n), або всi yi = 0 (i = 1, n). Нехай серед чисел xi (i = 1, n) i серед чисел yi (i = 1, n) є хоч по одному, вiдмiнному вiд нуля, числу, i нехай

ai =	|xi|	1/p	, bi =	|yi|	1/q	.
	n			n
	i=1 |xi|p			i=1 |yi|q
	P			P

Тодi, скориставшись нерiвнiстю Юнга, для i = 1, n, маємо

n

|xi||yi|

1/q

≤

|xi|p

+

|yi|q

.

1/p

n

n

n

i=1 |xi|p

i=1 |yi|q

p i=1 |xi|p

q i=1 |yi|q

P

P

P

P

Просумувавши цi нерiвностi, отримаємо

n

n

n

1/q

+ = 1.

iP1/p

=1 |xiyi|

≤

1 1

i=1 |xi|p i=1 |yi|q

p q

P

P

14

Звiдси безпосередньо випливає нерiвнiсть (1.3). ♦

3. Нерiвнiсть Кошi-Буняковського.Для будь-яких xi, yi

R (i = 1, n) виконується нерiвнiсть

v v

nu n u n

XX X

i=1	|xiyi| ≤ ui=1 xi2ui=1 yi2.	(1.4)
	t t

4. Нерiвнiсть Мiнковського.Якщо p ≥ 1, то для будь-яких

xi, yi R (i = 1, n) виконується нерiвнiсть

n	|xi + yi|p 1/p	≤	n	|xi|p 1/p	+	n	|yi|p 1/p	(1.5)
i=1			i=1			i=1
X			X			X

Доведення. Для p = 1 нерiвнiсть (1.5) очевидна. Нехай p > 1, a q таке, що p1 + 1q = 1, тобто q = p −p 1. Тодi, застосу-

вавши нерiвнiсть Гельдера до кожного доданка правої частини суми

nn

XX

|xi + yi|p ≤	|xi + yi|p−1(|xi| + |yi|) =
i=1	i=1
n	n

XX

= |xi + yi|p−1|xi| + |xi + yi|p−1|yi|,

		i=1			i=1
маємо
n	|xi	+ yi|p ≤	n	|xi|p	n		+
i=1			i=1		1/p i=1 (|xi + yi|p−1)q 1/q
X			X		X
	n		n			=
+ i=1		|yi|p 1/p i=1 (|xi + yi|p−1)q 1/q
	X		X

15

=	n	|xi + yi|p	p−1	n	|xi|p		1/p	n	|yi|p	1/p	.
	i=1		p	i=1			+	i=1
	X			X				X

Роздiливши обидвi частини останньої нерiвностi на

n

p−1

Xi

|xi

+ yi|p

p ,

=1

дiстанемо нерiвнiсть (1.5).

♦

5. Нерiвнiсть Кошi-Буняковського.Для будь-яких xi, yi

R (i =

1, n

) виконується нерiвнiсть

v

v

+ v

n

(xi + yi)2

n

(xi)2

n

(yi)2.

(1.6)

ui=1

≤ ui=1

ui=1

uX

uX

uX

t

t

t

Нехай lp, де p ≥ 1 – множина послiдовностей дiйсних чисел

∞

(xn) таких, що n=1 |xn|p

< +∞.

Якщо p ≥ 1, то для будь-яких

6.

P

Нерiвнiсть Мiнковського.

послiдовностей (xn), (yn) lp виконується нерiвнiсть

∞

1

∞

1

∞

1

(1.7)

n=1

|xn + yn|p p

≤ n=1 |xn|p p +

n=1 |yn|p p

X

X

X

Доведення. Якщо (xn), (yn) lp, то ряди

∞∞

XX

|xn|p, |yn|p

n=1 n=1

збiгаються. Позначимо їх суми вiдповiдно через A i B. Оскiльки цi ряди мають невiд’ємнi члени, то послiдовностi їх часткових сум неспаднi i для кожного n

n

n

XX

|xk|p ≤ A,	|yn|p ≤ B.
k=1	k=1

16

З другого боку, скориставшись нерiвнiстю (1.5), для n-ої час-

ткової суми ряду

∞

X

|xn + yn|p

n=1

матимемо

n		1	1		p
k=1
	|xk + yk|p ≤ Ap		+ B p		.
X
А отже, останнiй ряд збiгається i
∞		1	1		p
n=1	|xn + yn|p ≤ Ap		+ B p		.
X
Звiдси вже безпосередньо випливає нерiвнiсть (1.7).						♦

7.Нерiвнiсть Кошi.Для будь-яких послiдовностей (xn), (yn)

зl2 виконується нерiвнiсть

∞	v			v
	u ∞			u ∞
X	uX			uX
n=1	|xnyn| ≤ tn=1		(xn)2tn=1(yn)2.				(1.8)

Для доведення досить скористатись нерiвнiстю (1.4) i вiдповiдними властивостями збiжних рядiв.

Нехай R[a;b] – множина iнтегровних на вiдрiзку [a; b] функцiй.

8. Нерiвнiсть Гельдера (для iнтегралiв). Якщо p > 1, q > 1 i p1 + 1q = 1, то для будь-яких функцiй f, g R[a;b] виконується нерiвнiсть

Z	b	Z	b	1	Z	b	1
	|f(x)g(x)|dx ≤		|f(x)|pdx			|g(x)|qdx
				p			q	(1.9)
a		a		a

17

Доведення. Нехай f i g двi довiльнi функцiї з R[a;b]. Тодi iнтегровними на вiдрiзку [a; b] будуть функцiї |f|p i |g|q, а отже, у випадку, коли iнтеграли

bb

ZZ

|f(x)|pdx,

|g(x)|qdx

(1.10)

aa

вiдмiннi вiд нуля, функцiї

ab	|f(x)|	1	,	ab	|g(x)|	1
	|f(x)|pdx p				|g(x)|qdx q
R				R

належaть множинi R[a;b]. Скориставшись нерiвнiстю Юнга, матимемо: для всiх x [a; b] виконується нерiвнiсть

	|f(x)|	·		|g(x)|	≤		|f(x)|p	+		|g(x)|q
b	1		b	1		b			b
	p			q						|g(x)|qdx
a	|f(x)|pdx a			|g(x)|qdx		p a	|f(x)|pdx q a
R			R			R			R

Проiнтегрувавши останню нерiвнiсть у межах вiд a до b, дiстанемо

	b
	Ra	|f(x)||g(x)|dx		≤
b		1 b	1
R |f(x)|pdx p R |g(x)|qdx p

aa

	b			b
≤	Ra |f(x)|pdx		+	Ra |g(x)|qdx		=	1	+	1	= 1.
	b			b			p		q
	p Ra	|f(x)|pdx q Ra			|g(x)|qdx

18

Звiдси уже безпосередньо випливає нерiвнiсть (1.9). Якщо ж хоча б один з iнтегралiв (1.10) дорiвнює нулю, то

Za

b

|f(x)||g(x)|dx = 0.

Отже, i у цьому випадку нерiвнiсть (1.9) має мiсце.

9. Нерiвнiсть Кошi (для iнтегралiв). Для будь-яких фун-

кцiй f i g з множини R[a;b] виконується нерiвнiсть

b

f(x)

g(x)

dx

v

v

(1.11)

b

f2(x)dx

b

g2(x)dx

Z

|

||

|

≤ uZ

uZ

a

ua

ua

u

u

t

t

10. Нерiвнiсть

Мiнковського

(для iнтегралiв).

Якщо

p ≥ 1, то для будь-яких функцiй f, g з множини R[a;b]

вико-

нується нерiвнiсть

b

Z |f(x) + g(x)|pdx

1

≤

p

a

Z

b

1

Z

b

1

≤

|f(x)|pdx

|g(x)|pdx

p

+

p

(1.12)

a

a

Доведення. Для p = 1 нерiвнiсть (1.12) очевидна.

Нехай

p > 1, a q таке, що

1

+ 1 = 1, тобто q =

p

. Тодi, застосу-

p

−

1

p

q

вавши нерiвнiсть Гельдера до правої частини нерiвностi

b

b

Za

|f(x) + g(x)|pdx ≤ Za

|f(x) + g(x)|p−1|f(x)|dx +

19

b

Z

+|f(x) + g(x)|p−1|g(x)|dx,

a

матимемо

b			b
Z |f(x) + g(x)|pdx ≤								1
			Z |f(x)|pdx p
a		a
b							b
Z (|f(x) + g(x)|p−1)qdx				1			Z	|g(x)|pdx	1
				q	+				p
a						a
b							b			p−1
Z (|f(x) + g(x)|p−1)qdx				1			Z	|f(x) + g(x)|pdx
				q	=					p
a						a
b		b
Z	1	+ Z |g(x)|pdx						1
	|f(x)|pdx p							p .
a		a
Подiливши обидвi частини останньої нерiвностi на
	b						p−1
	Z |f(x) + g(x)|pdx
							p ,
	a
дiстанемо нерiвнiсть (1.12).
Приклад 3. Нехай p ≥ 1. Довести, що функцiя
	d((x1, x2, . . . , xn)), (y1, y2, . . . , yn)) :=
			=		n			1		(1.13)
				i=1 |xi − yi|p p
					X

надiляє метрикою множину Rn.

Розв’язання. Виконання перших двох аксiом вiдстанi є очевидним. Далi, скориставшись нерiвнiстю Мiнковського (1.5),

20