metritchni_proct

точки прямої x = 2 ?

Рис. 7

Звичайно такими вiзуальними спостереженнями не можна скористатись при побудовi загальної теорiї. Разом з тим якраз вони пiдказали, як означити основнi топологiчнi поняття у довiльному метричному просторi.

Нехай маємо метричний простiр (X, d), i нехай x◦ X, a r — довiльне додатне число.

Означення 3.1. Вiдкритою кулею (або кулею) з центром у точцi x◦ радiуса r називають множину всiх тих точок множини X, вiдстань яких до точки x◦ менша r, i позначають B(x◦, r), тобто

n o

B(x◦, r) := x | x X, d(x◦, x) < r .

Множину

n

o

B(x◦, r) := x | x X, d(x◦, x) ≤ r

61

називають замкненою кулею з центром у точцi x◦ радiуса r, а множину

n

o

S(x◦, r) := x | x X, d(x◦, x) = r

– сферою з центром у точцi x◦ радiуса r.

Наприклад, множини

n o

x | x R, |x − 1| < 2 = (−1; 3),

n o n o

x | x R, |x−1| ≤ 2 = [−1; 3], x | x R, |x−1| = 2 = {−1; 3}

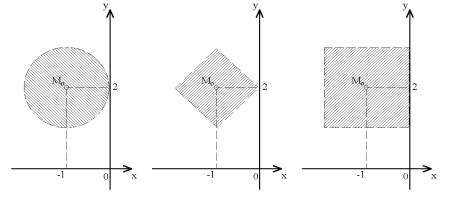
є вiдповiдно вiдкрита, замкнена кулi i сфера з центром у точцi x◦ = 1 i радiусом r = 2 у метричному просторi R з природною метрикою, а множини

n(x, y) | (x, y) R2, p						< 1o,
				(x + 1)2 + (y − 2)2
n(x, y) | (x, y) R2, |x + 1| + |y − 2| < 1o,
n(x, y) | (x, y) R2, max(|x + 1|, |y − 2|) < 1o,
є вiдкритими кулями з	центром			M◦(−1; 2)	у точцi радiуса		r = 1
		2
у метричному просторi R			вiдповiдно з метриками

p

d1((x1, y1), (x2, y2)) = (x1 − x2)2 + (y1 − y2)2, d2((x1, y1), (x2, y2)) = |x1 − x2| + |y1 − y2)|,

d3((x1, y1), (x2, y2)) = max(|x1 − x2|, |y1 − y2|).

Їх зображення на кординатнiй площинi має вигляд (pис.8 – 10).

62

					Рис. 8 – 10
Приклад 1. Нехай множина C[0;1]									надiлена рiвномiрною ме-
трикою. Чи належать точки						f1(x) = x2 − x +						1	,
												2
1			1			1			2					1
f2(x) =		x2 − x +			, f3(x) =			x2 − x +			, f4	(x) = x3 −
	2			2			2			3				2

вiдкритiй кулi B(x2, 1) ?

Розв’язання. У метричному просторi C[0;1] з рiвномiрною метрикою вiдкритою кулею B(x2, 1) є множина всiх тих неперервних на вiдрiзку [0; 1] функцiй f, для яких

max |f(x) − x2| < 1,

x [0;1]

тобто множина неперервних на вiдрiзку [0; 1] функцiй, графiк кожної з яких попадає у смугу

n o

(x, y) | 0 ≤ x ≤ 1, x2 − 1 < f(x) < x2 + 1

(pис.11).

63

Рис. 11

Для першої точки матимемо

d

x2, x2

−

x

+

1

max

|

x

−

1

|

=

1

< 1,

2

2

(

2) = x

[0;1]

тобто f1 B(x2, 1), для другої —

d(x2,

1

x2

−

x

+

1

max

|

1

x2

+ x

−

1

|

=

1,

2

2

2) = x

[0;1]

2

тобто f2 6 B(x2, 1), для третьої —

d(x2,

1

x2

−

x

+

2

max

|

1

x2

+ x

−

2

|

=

5

,

3

6

2

3) = x

[0;1]

2

64

тобто f3 B(x2, 1), для четвертої —

d

x2, x3

−

1

max

|

x3

−

x2

−

1

| =

35

,

2

2

54

(

= x

[0;1]

тобто f4 B(x2, 1).

Приклад 2. Множина R надiлена метрикою: для будь-яких

x, y R

|x − y|

d(x, y) =

.

1 + |x − y|

1

1

Знайти перетин двох вiдкритих куль

B 0, 2

, B 1, 3

.

Розв’язання. За означенням

B 0,

1

= x

x

<

1

, B 1,

1

= x

x − 1|

<

1

.

1 +|

||x|

1 +| |x − 1|

2 n

2o

3

n

3o

Розв’язавши нерiвностi

|x|

<

1

,

|x − 1|

<

1

1|

3

1 + |x|

2 1 + |x −

1

1

1

3

дiстанемо B

0,

= (−1; 1),

B

1,

=

;

.

2

3

2

2

жиною

1

\

1

1

Отже, B 0,

2

B

1,

3

=

2

; 1 .

Врахувавши, що мно-

розв’язкiв нерiвностi

|x − a|

< r

a−

1 + |x − a|

рiвнянь

1

r

r

1 − r

; a+ 1 − r

при r <

є iнтервал

, i розв’язавши систему

a −

r

1

=

,

1 − r

2

a +

r

= 1,

1 − r

65

	3		1		1					1			3		1
дiстанемо a =		, r =		, тобто B	0,		\B		1,		= B			,			.
	4		5			2				5			4		5
Приклад 3. Нехай множина					N надiлена метрикою
			d(m, n) =		|m − n|			,
					mn

i нехай m◦ - фiксоване натуральне число. Довести, що вiдкрита куля B(m◦, r) мiстить всi натуральнi числа за винятком мо-

								1
жливо скiнченного числа їх, якщо r ≥										, i мiстить скiнченне
									m◦
число чисел, якщо r <		1	.
	m◦
Розв’язання. За означенням
B(m	, r) = n n			N		,	|	n − m◦|			< r ,
◦	n							nm◦			o
тобто кулi B(m◦, r) належать					всi тi натуральнi числа, якi є
розв’язками нерiвностi
		|n − m◦| < nm◦r
або системи нерiвностей
	m◦ < n(1 + rm◦),
	n(1 − rm◦) < m◦.
Першу нерiвнiсть	системи задовольняють всi натуральнi числа,
для яких					m◦
		n >						.
				1 + rm◦

Множина розв’язкiв другої системи залежить вiд знаку числа

1 − rm◦. Якщо 1 − rm◦ ≤ 0 або r ≥ 1 , то для будь-якого на- m◦

турального n n(1 − rm◦) < m◦ i множиною розв’язкiв системи

66

є множина			nn n >		m◦
						o = B(m◦, r) ,
					1 + rm◦
							m
тобто B(m		, r) мiстить		всi натуральнi числа, якщо					◦	< 1,
	◦						1 + rm◦
										m◦
i мiститьmвсi натуральнi числа крiм чисел 1, 2, . . . , h											i,
								1 + rm◦
якщо	◦		≥ 1. Якщо ж 1−rm◦ > 0, то розв’язками системи
	1 + rm◦

будуть всi тi натуральнi числа, якi задовольняють нерiвнiсть

		m◦			< n <		m◦	,
Отже,		1 + rm◦				1 − rm◦
	n N,
B(m◦, r) = nn					m◦				m◦
					1 + rm◦ < n <			1 − rm◦ o.
Нехай A – множина			точок метричного простору (X, d) i x◦

X. Домовимось надалi замiсть термiну "вiдкрита куля"вживати термiн "куля".

Означення 3.2. Точка x◦ називається внутрiшньою точкою множини A, якщо iснує куля B(x◦, r), яка є пiдмножиною множини A. Множину всiх внутрiшнiх точок множини A називають внутрiшнiстю множини A i позначають A◦.

Означення 3.3. Точка x◦ називається межовою точкою множини A, якщо кожна куля B(x◦, r) мiстить як точки з множини A, так i точки, якi їй не належать. Множину всiх межових точок множини A називають межею множини A i позначають ∂A.

Означення 3.4. Точка x◦ називається зовнiшньою точкою для множини A, якщо iснує куля B(x◦, r), яка не мiстить жодної точки з множини A. Множину всiх зовнiшнiх точок для множинi A називають зовнiшнiстю множини A i позначають Aз.

67

Означення 3.5. Точка x◦ називається точкою дотикання для множини A, якщо кожна куля B(x◦, r) мiстить принаймнi точку з множини A. Множину всiх точок дотикання для множини A називають замиканням множини A i позначають A.

Означення 3.6. Точка x◦ називається граничною точкою для множини A, якщо кожна куля B(x◦, r) мiстить принаймнi одну точку множини A, вiдмiнну вiд x◦. Множину всiх граничних точок для множини A називають похiдною множиною множини A i позначають A0.

Означення 3.7. Точка x◦ називається iзольованою точкою множини A, якщо iснує куля B(x◦, r), яка крiм точки x◦ не мiстить жодної точки з множини A.

Так, для множини

n o

A = (x, y)| |x| + |y| < 1, або |x −2| = 0, або |x −3|+ |y − 1| = 0

(pис.7) точок метричного простору R2 з евклiдовою метрикою

	точки M1			1	,		1	, M2(1, 0), M3(2, 0)								є вiдповiдно внутрiшною,
			3				3
																	, а точка		– iзо-
		граничною для множини
	межовою i															A2		M4(3, 1)
	льованою точкою цiєї множини.
	Справдi, оскiльки вiдстань вiд точки M1 до прямої x + y = 1
			1					1			1		1
	дорiвнює	3√					, то куля B			,		,				є пiдмножиною множини
									3		3		6
						2

A. Якими б не були кулi B((1, 0), r), B((2, 0), ρ), кожна з них мiстить як точки з множини A, так i точки, що їй не належать, а також кожна з них мiстить принаймнi по однiй точцi, вiдмiннiй вiд (1, 0) для першої i вiд (2, 0) для другої кулi.Отже, точки M2 i M3 є одночасно i межовими i граничними. Нарештi куля

B (3, 1), 12 крiм точки M4 не мiстить жодної точки з множини

68

A. Очевидно, що для множини A

A◦ = n(x, y) |	|x| + |y| < 1o
∂A = n(x, y) |	|x| + |y| = 1, або |x − 2| = 0, |x − 3| + |y − 1| = 0o
A0 = n(x, y) |	|x| + |y| ≤ 1 або |x − 2| < 0o

n o

A = (x, y) | |x|+ |y| ≤ 1, або |x −2| = 0, або |x −3|+ |y −1| = 0

Aз = R2 \ A.

Очевидно, що A◦ A0 A (кожна внутрiшня точка множини A є граничною, а кожна гранична є точкою дотикання), A◦ A ( кожна внутрiшня точка множини A належить множинi A), ∂A A (кожна межова точка є точкою дотикання), A A (кожна точка множини A є її точкою дотикання).

Серед видiлених класiв точок особлива роль за внутрiшнiми i граничними, оскiльки через них означаються два важливих класи множин.

Означення 3.8. Множина G точок метричного простору X називається вiдкритою, якщо кожна її точка внутрiшня. Кожну вiдкриту множину, якiй належить точка x◦, називають околом цiєї точки.

Означення 3.9. Множина F точок метричного простору X називається замкненою, якщо вона мiстить всi свої граничнi точки, а замнену множину без iзольованих точок називають досконалою.

Приклад 4. Довести, що кожна вiдкрита куля є вiдкритою множиною.

69

Розв’язання. Нехай маємо метричний простiр (X, d), i нехай B(x◦, r) куля з центром у точцi x◦ i радiусом r, тобто

B(x◦, r) = nx	x X, d(x◦, x) < ro.

Якщо x0 довiльна, але фiксована точка, яка належить цiй кулi, то d(x◦, x0) < r. Вiзьмемо число r◦, яке задовольняє нерiвнiсть

0 < r◦ < r − d(x◦, x0), i розглянемо кулю B(x0, r◦). Тодi для будь-якого x B(x0, r◦)

d(x◦, x) ≤ d(x◦, x0) + d(x0, x) < d(x◦, x0) + r − d(x◦, x0)

тобто x B(x◦, r), а отже, B(x0, r◦) B(x◦, r). Цим доведено, що кожна точка кулi B(x◦, r) є внутрiшньою, тобто куля B(x◦, r) – вiдкрита множина.

Приклад 5. Довести, що кожна замкнена куля є замкненою множиною.

Розв’язання. Припустимо, що iснує такий метричний простiр (X, d) i у ньому замкнена куля B(x◦, r), яка не є замкненою множиною, тобто iснує точка x0 X, яка є граничною для

множини B(x◦, r), але x0 / B(x◦, r). Якщо x0 / B(x◦, r), то d(x◦, x0) > r, а отже, iснує число r◦ > 0, що r◦ < d(x◦, x0) − r.

Розглянемо кулю B(x0, r◦), i нехай x B(x0, r◦). Тодi для точок x◦, x0, x маємо

d(x◦, x0) ≤ d(x◦, x) + d(x, x0)

або

d(x◦, x) ≥ d(x◦, x0) − d(x, x0).

Врахувавши, що d(x0, x) < r◦ i d(x◦, x0) − r◦ > r, маємо: d(x◦, x) > r. Отже, iснує куля B(x0, r◦), жодна точка якої не належить кулi B(x◦, r). Тодi точка x0 не є граничною для замкне-

ної кулi B(x◦, r), що суперечить нашому припущенню. Одержане протирiччя свiдчить про те, що наше припущення невiрне,

70