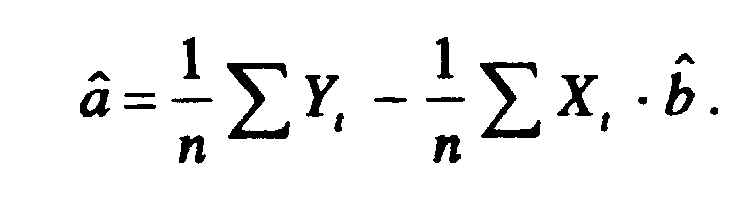Раздел 7_______________________________________

СТАТИСТИЧЕСКИЙ АНАЛИЗ СВЯЗЕЙ

Раздел 7 пособия ознакомит вас с некоторыми положе­ниями регрессионно - корреляционного анализа взаимосвязей процессов и явлений, составляющего важную познавательную задачу статистики.

Эта задача решается статистикой в определенной последовательности, начиная с наличия связи, выявления ее направления и формы, нахождения аналитического выражения и кончая измерением тесноты связи между изучаемыми признаками. Вы найдете здесь необходимую теорию и прак­тические рекомендации по расчету показателей связи между количест­венными и атрибутивными признаками и указания по их проверке на зна­чимость (существенность)

В результате изучения этого раздела вы сможете

1. обосновать основные положения теории регрессионно - корреляцион­ного анализа связей явлений, определить его задачи, последователь­ность этапов проведения, их содержание и методику расчета показа­телей регрессии и корреляции;

2. объяснить специфику проведения такого анализа по количественным и атрибутивным признакам;

3. провести анализ корреляционной связи между признаками в рамках сквозного контрольного задания;

4. обобщить изученные вами по предыдущим разделам и темам мето­ды статистического изучения общественных явлений во всей их взаимосвязи и взаимообусловленности

Тема 24

ОСНОВНЫЕ ПОНЯТИЯРЕГРЕССИОННО-КОРРЕЛЯЦИОННОГО АНАЛИЗА

После изучения этой темы вы сможете:

1. дать сравнительную характеристику всех изученных вами по преды­дущим разделам и темам методов статистического изучения взаимо­связей различных процессов и явлений;

2. раскрыть природу корреляционных связей процессов и явлений и обосновать ос­новные понятия регрессионно - корреляционного анализа.

Как известно все процессы и явления в природе и обществе взаимосвязаны и взаимообусловлены.

Существует множество изученных видов и форм связей между ними, различающихся по своей сущности и характеру, по направлению и тесноте, по аналити­ческому выражению и т.д. Статистика и изучает эти связи, используя различные методы и приемы. Этому служат уже изученные нами группировка и сводка, абсолютные и относительные величины, средние и показатели вариации, динамические ряды и индексы.

В этом разделе объектом нашего исследова­ния выступают особые связи явлений - корреляционные связи, при которой значениям одной переменной соответствуют не значения другой переменной, а разные значения другой переменной. Корреляционные связи позволили рассмотреть связи между процессами и явлениями со всем с другой точки зрения. В каком – то смысле их антиподом является функциональная связь хорошо известная вам, в основном из курса математики, функциональная связь меж­ду признаками, когда каждому возможному значению одного из них соот­ветствует одно, вполне определенное, значение другого. Это строгая и полная связь (зависимость) в отличие от статистической, вероятностной, корреляционной. Именно корреляционные связи присущи подавляющему большинству процессов и явлений. Особая роль в изучении статистических, вероятностных связей при­надлежит регрессионно-корреляционному анализу (РКА).

РКА заключается в построении и анализе экономико-статистической модели в виде уравнения регрессии, характери­зующего зависимость признака от определяющих его факторов.

Первая его составляющая - регрессионный анализ - связана с построением модели - уравнением регрессии,

вторая - корреляционный анализ – в котором главное это оценка тесно­та связи признаков. РКА предполагает следующие этапы: постановка задачи; ее спецификация; сбор информации и ее первичная обработка; построение мо­дели; проверка модели на достоверность; оценка и анализ модели.

На первом этапе формируются основные направления всего анализа, определяется методика оценки результативно­го показателя и перечень наиболее существенных его факторов и выбор формы связи.

Очень важным этапом РКА является построение модели (уравнения регрессии). Выбор формы связи признаков осуществляется на основании исходных эмпирических данных и теоретического обоснования рабочей гипотезы о взаимодействии признаков.

Связи в экономических процессах и явлениях, чаще всего, изучаются по уравнению пря­мой так как эта форма связи наиболее изучена и существуют хорошо отработанные методики расчета. Это линейная зависимость или линейная, связь, которая предполагает равномерное по­вышение результативного признака в зависимости от роста факторного.

Уравнение прямой (равно и любой кривой) в рамках РКА именуется урав­нением связи или регрессии, а геометрическое ее истолкование - линией регрессии.

Уравнение парной линейной регрессии имеет следующий вид:

у_х = а₀ + вх,

где х -факторный признак; а₀ и в - параметры уравнения.

В математическом смысле параметр а является отрезком ординаты при х=0, а параметр в - тангенсом угла наклона прямой.

Экономический же их смысл сле­дующий: а характеризует значение результативного признака вне зави­симости от взятого факторного; а, в показывает, насколько в среднем изменится признак у при изменении признака х на одну единицу его измерения, и называ­ется коэффициентом регрессии. На его основе рассчитывается ряд коэффициентов, таких как коэффициенты детерминации, эластичности и ряд других. Он показывает, на сколько процентов в среднем изменится величина функции у при изменении факторного при­знака х на один процент относительно своей средней. Параметры нахо­дятся из системы двух нормальных уравнений для парной линейной рег­рессии, полученных на основе выравнивания по методу наименьших квадратов МНК:

Первая задача корреляции заключается в выявлении на основе значительного числа наблюдений того, как меняется в среднем результативный признак в связи с изменением одного или нескольких факторов.

Вторая задача состоит в определении степени влияния искажающих факторов.

Первая задача решается определением уравнения регрессии и носит название регрессионного анализа.

Вторая - определением различных показателей тесноты связи и называется собственно и корреляционным анализом.

При изучении влияния одних признаков явлений на другие из цепи признаков, характеризующих данное явление, выделяются факторные и результативные признаки. Выделение признаков ведется логическим анализом.

Например, производительность труда зависит от стажа работы, разряда рабочих. Значит, производительность труда – результативный (функциональный) признак, а стаж, разряд рабочего - факторный признак (аргумент).

Связь между двумя взаимосвязанными признаками легко изобразить графически. Для этого результативный признак (функцию) обозначают y, а факторный (аргумент) - x.

Пару чисел легко представить на плоскости, образуемой системой прямоугольных координат, при этом факторный признак откладывается на оси абсцисс и результативный - на оси ординат.

Если одному значению факторного признака соответствует только одно значение результативного, то такая связь называется функциональной. Функциональные связи легко представить формулами. Например, зависимость силы тока от величины напряжения к сопротивлению в электрической цепи (закон Ома).

Связь между случайными величинами называется стохастической. Эта связь характеризуется тем, что результативный признак не полностью определяется факторным признаком, его влияние проявляется в среднем при достаточно большом числе наблюдений.

Пример

Имеются следующие данные о разряде рабочего и среднемесячной заработной плате.

Таблица 18

Разряд	1	1	2	2	2	2	3	3	3	3
Среднемесячная з/п, р.	100	120	150	160	170	190	180	180	180	190
Разряд	4	4	4	4	4	5	5	6	6	6
Среднемесячная з/п, р.	180	240	250	300	300	280	280	340	360	410

Разряд11	2	2	2	2	3	3	3	3
Среднемесячная з/п, р.100120	150	160	170	190	180	180	180	190
Разряд44	4	4	4	5	5	6	6	6
Среднемесячная з/п, р.180240	250	300	300	280	280	340	360	410

Изобразим эти данные графически.

График 15

Видно, что одному значению аргумента (разряду) соответствует ряд распределения функции (зарплаты). Ряды распределения функции закономерно смещаются - зарплата в среднем увеличивается с повышением разряда. Найдем средние значения аргумента и функции.

Таблица 19

	1	2	3	4	5	6
	110	168	186	254	280	370

и т.п.

Нанесем на график и и соединим ломаной линией.

Эта линия изображает взаимосвязь между средними значениями аргумента и функции и называется эмпирической линией регрессии. Необходимо установить теоретическую линию регрессии, т.е. установить функцию, связывающую результативный и факторный признаки. Полученная ломаная регрессия (рис. 8) может помочь в выборе функции. Увеличение или уменьшение результативного и факторного признаков в арифметической прогрессии означают, что сглаживание нужно производить по прямой . В этом случае эмпирические графики должны быть (рис.):

Если равноускоренное или равнозамедленное изменение функции то сглаживание можно провести по параболе второго порядка или по гиперболе.

.

График 19 График 20

Более сложные зависимости могут быть иллюстрированы параболой третьего порядка, логарифмической или показательной функцией.

Выбрав теоретическую функцию, описывающую корреляционную зависимость между результативным и факторным признаком, нужно рассчитать параметры уравнения регрессии. Расчет чаще всего производится по способу наименьших квадратов при использовании системы нормальных уравнений.

Эти системы различны для разного рода кривых:

1. Прямая линия ;

2. Парабола второго порядка ;

3. Гипербола .

.

В нашем примере, используя в качестве теоретической функции прямую , рассчитаем параметры уравнения.

Для этого определим .

Решив систему нормальных уравнений, найдем a  54, b  50.

Следовательно, уравнение имеет вид .

Значит, для рабочего 2 разряда зарплата по уравнению рассчитывается (р.) - что отличается от эмпирических данных.

Теснота или сила связи между двумя признаками может быть измерена эмпирическим корреляционным отношением ()

.

В случае прямолинейной связи тесноту можно определить с помощью коэффициента корреляции (r).

.

Коэффициент корреляции может изменяться от +1 до -1. Чем ближе значение r по абсолютной величине к единице, тем теснее связь. Если r > 0, то связь между факторным и результативным признаком прямо пропорциональная, если r < 0, то - обратно пропорциональная.

В нашем примере:

Значит, связь прямо пропорциональная, достаточно тесная.

Задание

Приведите пример корреляционных по своей сути связей.

Подумайте какая по форме связь между:

Заработной платой и количеством продукции при;

сдельной формой оплаты труда,

повременной оплатой труда

при фиксированном окладе

Регрессионные методы позволяют выявить связи между переменными, причем особенно эффективно, если эти связи не совершенны или не имеют точного функционального описания между этими переменными. В эконометрическом анализе используются независимые переменные х_i и одна зависимая переменная y. Регрессией в общем виде представляется функцией следующего вида

где - известные коэффициенты регрессии;

x_i - переменная. В эконометрическом анализе переменные представляют собой статистические данные, например стоимость товара, объем продаж, курс валюты. Так как эти данные чаще всего «привязаны» ко времени, то в эконометрических моделях используют и другие обозначения переменных, такие как X_t, где индекс t обозначает, что мы используем временной ряд.

 - неувязка (ошибка, отклонение, возмущение), обусловленная недостаточной пригодностью модели и ошибкой данных. Обычно эти причины являются смешанными.

Обозначения в модели интерпретируются достаточно просто. Например, сумму

можно представить как сумму произведений коэффициента b и переменной х

.

В последующем для упрощения выражений знак суммы мы будем обозначать без индексов, как .

В том случае, если исследуется влияние одной переменной или фактора, то выражение упрощается к виду

Выражение представляет собой линейную однофакторную регрессию. Геометрический смысл уравнения поясним на рис.

Пусть мы имеем четыре измерения переменнойх, которые имеют конкретное значение р_{1 ,}р₂, р₃, р₄. Этим значениям соответствуют определенные значения зависимой переменной y. Тогда уравнение регрессии 2.2 представляет собой прямую линию проведенную определенным образом через точки р_{1 ,}р₂, р₃, р₄. Так как истинное значение переменной нам неизвестно, то мы предполагаем, что оно располагается на этой прямой в точках Q₁, Q₂, Q_3, Q₄. Свободный член а уравнения 2.2 имеет реальный экономический смысл. Это минимальное или максимальное значение зависимой переменной (результативного признака).

Коэффициент b представляет собой постоянную величину, равную отношению

Природа ошибки 

Существует, по крайней мере, две причины появления в модели этой ошибки или как ее еще называют – возмущение.

1. Наша модель является упрощением действительности и на самом деле есть еще и другие параметры, от которых зависит переменная y. Например, расходы на питания в семье зависят от размера заработной платы членов семьи, национальных и религиозных традиций, уровня инфляции и т.д.

2. Скорее всего, наши измерения содержат ошибки наблюдения. Например, данные по расходам семьи на питание составляются на основе а опроса и эти данные не всегда отражают истинное значение параметров. Необходимо отметить, что любые формы наблюдения, включая документальный содержат ошибки.

Таким образом, можно считать, что ошибка  есть случайная величина с некоторой функцией распределения.

Задание

Известно, что спрос связан с предложением, что может составить ошибку  влияющей на спрос.

Для нахождения коэффициентов уравнений и используется метод наименьших квадратов. Сущность метода заключается в том, чтобы минимизировать сумму квадратов отклонений

,

где - значение результата, вычисленное по уравнению (2) в точке x_i ;

y_i - экспериментальное значение результата в этой же точке.

Рассмотрим задачу «наилучшей» аппроксимации набора наблюдений Y_t,, t = 1,..., n, линейной функцией (2.2) минимизацией функционала

Запишем необходимые условия экстремума

Раскроем скобки и получим стандартную форму нормальных уравнений (для краткости опустим индексы суммирования у знака суммы):

а, b – решения системы (2.4) можно легко найти:

Порядок построения регрессионной модели рассмотрим на следующем примере.

В таблице представлены статистические данные о расходах на питание и душевом доходе для девяти групп семей. Требуется проанализировать зависимость величины расходов на питание от величины душевого дохода.

В соответствии с этим первый показатель будет результативным признаком, который обозначим у, а другой будет факторным признакам, или просто фактором, и мы обозначим его соответственно х₁ . Это обозначение не случайно, в последующем примере мы рассмотрим более сложную модель, в которой будет два фактора х₁ и х₂.

Таблица 19

Номер группы	Расход на питание (у)	Душевой доход (х1)
1	433	628
2	616	1577
3	900	2659
4	1113	3701
5	1305	4796
6	1488	5926
7	1646	7281
8	1914	9350
9	2411	18807

ер группыРасход на питание (у)Душевой доход (х₁)

1433628

26161577

39002659

11133701

513054796

614885926

716467281

819149350

9241118807

Рассмотрим однофакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода семей (х₁).

Расчеты проведем в таблице.

Таблица 20

Номер группы	Расход на питание (у)	Душевой доход (х1)	Y Х1	Х1^2
1	433	628	271924	394384
2	616	1577	971432	2486929
3	900	2659	2393100	7070281
4	1113	3701	4119213	13697401
5	1305	4796	6258780	23001616
6	1488	5926	8817888	35117476
7	1646	7281	11984526	53012961
8	1914	9350	17895900	87422500
9	2411	18807	45343677	353703249
	 = 11826	 = 54725	 = 98056440	 = 575906797

Номер группыРасход на питание (у)Душевой доход (х1)	Y Х1	Х12
1433628	271924	394384
26161577	971432	2486929
39002659	2393100	7070281
411133701	4119213	13697401
513054796	6258780	23001616
614885926	8817888	35117476
716467281	11984526	53012961
819149350	17895900	87422500
9241118807	45343677	353703249
 = 11826 = 54725	 = 98056440	 = 575906797
Номер группыРасход на питание (у)Душевой доход (х1)	Y Х1	Х1^2
1433628	271924	394384
26161577	971432	2486929
39002659	2393100	7070281
411133701	4119213	13697401
513054796	6258780	23001616
614885926	8817888	35117476
716467281	11984526	53012961
819149350	17895900	87422500
9241118807	45343677	353703249
 = 11826 = 54725	 = 98056440	 = 575906797

Используя данные таблицы, получим систему уравнений:

Можно найти значения коэффициентов по формулам , но мы покажем как можно использовать более общий подход к решению задачи по правилу Крамера, для этого найдем значения определителей системы :

Тот же результат можно получить, используя следующие формулы

Таким образом, модель имеет вид:

y = 660,11 + 0,108 Х1

Уравнение называется уравнением регрессии, коэффициент b — коэффициентом регрессии. Направление связи между у и x₁ определяет знак коэффициента регрессии а₁. В нашем случае данная связь является прямой и положительной.

Вычислим дисперсии оценок а и b. Известно, что дисперсии оценок а и b можно определить как

где - дисперсия ;

отклонения исходной выборки от среднего значения;

, среднее значение;

- значения расходов на питание, вычисленные по модели.

Для проведения расчетов дисперсий полученных оценок используем таблицу.

Таблица 21

№№	Y	X	X^2
1	433	628	394384	727	-294	86436	-5453	29730362
2	616	1577	2486929	830	-214	45796	-4504	20282013
3	900	2659	7070281	947	-47	2209	-3422	11707042
4	1113	3701	13697401	1059	54	2916	-2380	5662285
5	1305	4796	23001616	1178	127	16129	-1285	1650083
6	1488	5926	35117476	1300	188	35344	-155	23887
7	1646	7281	53012961	1446	200	40000	1200	1441067
8	1914	9350	87422500	1669	245	60025	3269	10689267
9	2411	18807	353703249	2691	-280	78400	12726	161962388
	=11826	6081	=575906797			=367255		=243148394

YX	X^2
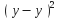
1433628	394384	727	-294	86436	-5453	29730362
26161577	2486929	830	-214	45796	-4504	20282013
39002659	7070281	947	-47	2209	-3422	11707042
411133701	13697401	1059	54	2916	-2380	5662285
513054796	23001616	1178	127	16129	-1285	1650083
614885926	35117476	1300	188	35344	-155	23887
716467281	53012961	1446	200	40000	1200	1441067
819149350	87422500	1669	245	60025	3269	10689267
9241118807	353703249	2691	-280	78400	12726	161962388
=118266081	=575906797			=367255		=243148394

Для определения параметров уравнения регрессии, выраженного сте­пенной функцией вида, следует привести ее к линейному виду путем логарифмирования. Это уравнение будет отличатся от уравнения парной линейной регрессии только логарифмами и, заменив в формулах его параметров на их логарифмы, получим расчетные формулы для параметров. Сама величина в, логарифмом не заменяется, в является, как было показано выше, коэффициентом регрессии. По нему рассчитывается коэффициент эластичности.

После построения модели уравнения регрессии она оценивается на предмет ее согласования с теоретическими соображениями относительно направления изменения у_х (знака параметра в) и характера его измене­ния уже в конкретных условиях исследуемой совокупности. В случае вы­явившегося несоответствия выясняются причины этого, среди которых могут быть ошибки в исходной информации и в расчетах, влияние не уч­тенных признаков, и, наконец, неправильно выбранная модель. В послед­нем случае строятся другие модели и отбирается та из них, которая обес­печивает меньшие отклонения теоретических уровней от эмпирических

Задание

Вам предлагается выписать и еще раз осмыслить все уравнения рег­рессии (модели), встретившиеся в тексте данной Темы, привести соот­ветствующие им системы нормальных уравнений и формулы определения параметров уравнений