matanaliz

111

16.6. Замiна змiнно¨ та iнтегрування частинами у визначених iнтегра-

ëàõ

Теорема 16.4. Нехай функцiя f неперервна на [a; b], ' неперервна i ма¹ неперервну похiдну на [®; ¯], '(®) = a, '(¯) = b. Òîäi

Zb Z¯

f(x) dx = f('(t)) ¢ '0(t) dt:

a ®

Приклад.

¼

¼

2

2

¡

¢

4

0 = 0;

5

0

0

cos3 x dx =

Z

1

¡

sin2 x cos x dx =

2

t = sin x;

t1 = sin

¼

3

=

Z

dt = cos t dt;

t2 = sin

2

= 1

Z

1 ¡ t2

dt = µt ¡ t3 ¶¯0 = 1 ¡ 3 ¡ (0 ¡ 0) = 3 :

1

¡

¢

3

¯

1

1

2

0

¯

Теорема 16.5. Нехай функцi¨

òà

¯

неперервнi на

i мають неперервнi

u

v

[a; b]

ïîõiäíi. Òîäi

Zb u(x)v0(x) dx = u(x)v(x) ab

¡ Zb v(x)u0(x) dx

a

¯

a

¯

Приклад.

Ze

ln x dx

1

=	2	u = ln x		du = dxx
	4	dv = dx		v = x

3

Ze

5 = x ln xje1 ¡ dx = e ¡ e + 1 = 1:

1

112

ÐÎÇÄIË 17

ЗАСТОСУВАННЯ IНТЕГРАЛIВ

17.1. Обчислення площ

6y = f(x)

G

-

a

b

1. Нехай область G обмежена графiком функцi¨ y = f(x), x 2 [a; b], причому

f(x) ¸ 0, та прямими y = 0, x = a, x = b. Тодi площа цi¹¨ областi обчислю¹ться за

формулою: Z b

SG = f(x) dx: (17.1.1)

a

Зокрема, якщо крива, що обмежу¹ область G, задана параметрично

x = x(t); y = y(t); t 2 [®; ¯]; x(®) = a; x(¯) = b;

òî ìà¹ìî	b f(x) dx =	2
SG =			x = x(t);
	Za	4	dx = x0(t) dt

3	=	Z®	Z®
		¯ f(x(t))x0(t) dt =	¯ y(t)x0(t) dt:
5

Отриму¹мо формулу:	Z®¯ y(t)x0(t) dt:
SG =						(17.1.2)
Приклад. Обчислимо площу елiпса		x2	+	y2	= 1. З мiркувань симетрi¨ достатньо
		2		2
		a		b

обчислити площу четвертинки елiпса i помножити ¨¨ на 4. В параметричнiй формi елiпс зада¹ться так: x = a cos t, y = b sin t, t 2 [0; 2¼].

	0						¼			¼
							2 sin2 t dt = 2ab			2 (1
S = 4		b sin t (	a sin t)dt = 4ab								cos 2t)dt =
Z	¼	¢ ¡					Z0			Z0	¡
	2
								¼
			= 2ab(t ¡	1				2	= ¼ab:
				2 sin 2t)¯0
							¯
							¯
							¯

113

2. Нехай область G обмежена графiками двох функцiй y = f(x) òà y = g(x), x 2 [a; b], причому f(x) ¸ g(x), та прямими x = a i x = b. Тодi площа цi¹¨ областi обчислю¹ться за формулою:

					SG = Zab (f(x) ¡ g(x)) dx:	(17.1.3)
			-
			-		r = f(')
	--		-		©©©©
-				©©
			©©
-		©
¯
- ©
©					-
©- ®

3. Нехай крива r = f('), ® · ' · ¯, задана у полярнiй системi координат. Площа сектора D, обмеженого променями ' = ® òà ' = ¯ i кривою r = f(') обчислю¹ться за формулою

					1		¯
						Z®		(f('))2 d':	(17.1.4)
					SD = 2
					@			¡
					@			¡
					@			¡
					@			¡
						@¡			a-
						¡@
					¡			@
					¡			@
					¡			@
					¡			@
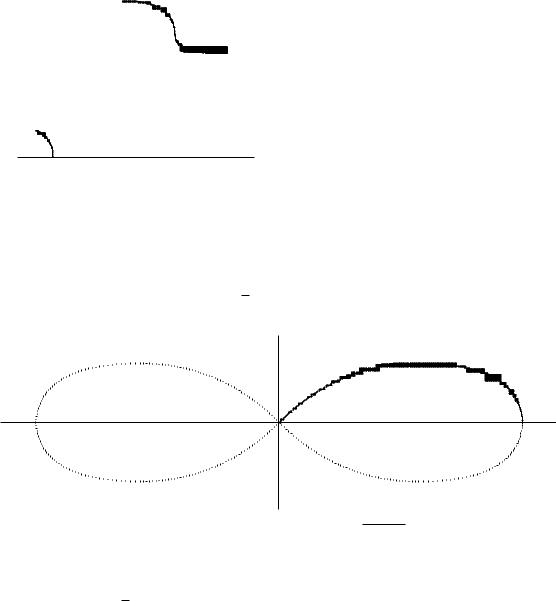
	Приклад. Обчислимо площу лемнiскати r = apcos 2'.
		1	Z0	¼		Z0	¼
				4			4	¼
	S = 4 ¢				r2 d' = 2a2			cos 2' d' = a2 sin 2'j04	= a2:
		2

17.2.Обчислення довжини дуги криво¨

17.2.1.Довжина дуги криво¨ в прямокутних координатах.

114

6

¢yi

-

a

¢xi

b

Нехай крива l задана рiвнянням y = f(x), äå x 2 [a; b]. Нехай

x0 = a; x1; : : : ; xn = b

розбиття сегмента [a; b]. Позначимо 4xi = xi ¡ xi¡1, 4yi = f(xi) ¡ f(xi¡1). Позна- чимо Mi = (xi; f(xi)), i = 1; 2; : : : ; n точки криво¨ l. З'¹днавши цi точки послiдовно, ми отрима¹мо ламану M1M2 : : : Mn , вписану в криву l. Âiäðiçîê Mi¡1Mi назива¹ться

ланкою ламано¨. 4si

4si = p(4xi)2 + (4yi)2 = s1 + µ4yi ¶24xi:

4xi

Означення 17.1. Якщо iсну¹ границя довжин всiх ламаних, вписаних в криву l,

при умовi, що максимальна довжина ланок пряму¹ до нуля, то ця границя назива¹ться

довжиною криво¨ l. Крива l назива¹ться кривою скiнченно¨ довжини.

Теорема 17.1. Нехай функцiя f : [a; b] ! R неперервна разом зi сво¹ю першою похiдною. Тодi крива l = f(x; y) j y = f(x); x 2 [a; b]g ма¹ скiнченну довжину, яка обчислю¹ться за формулою

s = Zab q

dx:

1 + (f0(x))2

(17.2.1)

Приклад. Знайти довжину дуги параболи y = x2, x 2 [0; 1].

s = Z0

1

q1 + (2x)2dx =

4 ³2xp1 + 4x2 + ln ¯2x + p1 + 4x2¯´¯0 =

1

¯

¯

¯

1

¯

¯

¯

= p5 + 1 ln(2 + p5): 2 4

a2(1 + cos ')2 + a2 sin2 'd' = 2a

115

17.2.2. Довжина дуги криво¨, задано¨ параметрично. Нехай

x = x(t); y = y(t); t 2 [®; ¯]

параметрично задана крива. Припустимо, що x(t), y(t) неперервнi функцi¨, якi мають неперервнi першi похiднi. Тодi довжина криво¨ обчислю¹ться за формулою

s = Z®¯ q

dt:

(x0(t))2 + (y0(t))2

(17.2.2)

Приклад. Знайти довжину дуги криво¨ x = et cos t, y = et sin t âiä t = 0 äî t = 1.

s = Z0

1 p

dt =

(et cos t ¡ et sin t)2 + (et sin t + et cos t)2

= Z01 etp

dt = p

etj01 = p

2

2

2(e ¡ 1):

Нехай

x = x(t); y = y(t); z = z(t) t 2 [®; ¯]

просторова параметрично задана крива. Припустимо, що x(t), y(t), z(t) неперервнi

функцi¨, якi мають неперервнi першi похiднi. Тодi довжина криво¨ обчислю¹ться за формулою

	s = Z®¯ q						dt:
			(x0(t))2 + (y0(t))2 + (z0(t))2					(17.2.3)
Приклад. Знайти довжину гвинтово¨ лiнi¨
x = a cos t; y = a sin t; z = amt ïðè					t 2 [0; 2¼]:
s = Z02¼	p	a2 sin2 t + a2 cos2 t + a2m2dt = a			1 + m2			¢ 2¼:
					p

17.2.3. Довжина дуги криво¨ в полярнiй системi координат. Нехай в полярнiй системi координат крива задана рiвнянням r = r('), ' 2 ['1; '2]. Тодi довжина

дуги криво¨ обчислю¹ться за формулою:

Z '2 p

s =

r2(') + (r0('))2d':

(17.2.4)

'1

Приклад. Знайти довжину кардiо¨ди

Z ¼ q

s = 2

r = a(1 + cos ').

Z ¼ p

2 + 2 cos 'd' =

0 0

= 4a Z0

r

2

d' = 4a Z0

cos 2 d' = 8a sin 2

0

= 8a:

¼

¼

¯

1 + cos '

'

' ¼

¯

¯

116

17.3. Обчислення об'¹мiв тiл за площами поперечних перерiзiв

Нехай ма¹мо тiло T , проекцi¹ю якого на вiсь Ox ¹ âiäðiçîê [a; b]. Позначимо через

Q(x0) площу перерiзу тiла T площиною x = x0, x0 2 [a; b]. Òîäi

V = Zab

Q(x) dx:

(17.3.1)

Приклад. Знайдемо об'¹м елiпсо¨да

x2

+

y2

+

z2

= 1:

2

2

2

a

b

c

Çàôiêñó¹ìî x0 = [2¡a; a] i розглянемо перерiз x = x0. Це елiпс, його площа дорiв-

íþ¹ S(x0) = ¼bc ³1 ¡

x0

´. Òîìó îá'¹ì åëiïñî¨äà äîðiâíþ¹

a2

a

= 3 ¼abc:

V = 2 Z0

¼bc µ1 ¡ a2

¶dx =

a2

µa2x ¡

3

¶¯¯0

a

x2

2¼bc

x3

¯

4

¯

17.4. Об'¹м тiла обертання

Нехай тiло T утворене обертанням графiка неперервно¨ невiд'¹мно¨ функцi¨ f : [a; b] ! R навколо осi Ox. Очевидно, що Q(x) = ¼f2(x). Òîìó îá'¹ì òiëà îá÷è-

слю¹ться за формулою:

V = ¼ Zab f2(x)dx:

(17.4.1)

Площа боково¨ поверхнi обчислю¹ться за формулою:

P = 2¼ Zab f(x)q

dx:

1 + (f0(x))2

(17.4.2)

Приклад. Нехай тiло

T утворене обертанням y = cos x, x 2 £¡

¼

;

¼

¤ навколо осi

Ox. Знайдемо його об'¹м:

2

2

¼

cos2 x dx = ¼ Z0

¼

µx +

¼

2

2

2

(1 + cos 2x) dx = ¼

1

2

=

¼

;

V = 2¼ Z0

2 sin 2x¶¯¯0

2

¯

¼

¯

P = 2 ¢ 2¼ Z0 2 cos x

1 + sin2 xdx =

p

¼

2

1

³

´

¯0

³

sin x

1 + sin2 x + ln j sin x + 1 + sin2 xj

= 2¼

p2 + ln(1 + p2) :

= 4¼ 2

p

p

¯

´

¯

¯

117

ÐÎÇÄIË 18

НЕВЛАСНI IНТЕГРАЛИ ТА IНТЕГРАЛИ, ЗАЛЕЖНI ВIД ПАРАМЕТРА

1.Iнтеграли по безмежному промiжку

2.Властивостi невласних iнтегралiв

3.Iнтеграли вiд необмежено¨ функцi¨

4.Iнтеграли, залежнi вiд параметра

18.1. Iнтеграли по безмежному промiжку

Нехай f : [a; +1) ! R неперервна функцiя.

Означення 18.1. Якщо iсну¹ скiнченна границя

Zb

lim f(x) dx;

b!+1

a

то вона назива¹ться невласним iнтегралом вiд функцi¨ f ïî ïðîìiæêó [a; +1) i познача¹ться

Za	f(x) dx =	b!+1 Za
+1		b
	def	lim f(x) dx:

При цьому говорять, що невласний iнтеграл çáiãà¹òüñÿ ÷è iñíó¹. Якщо ж границя

b

lim f(x) dx не iсну¹ чи безмежна, то кажуть, що невласний iнтеграл íå iñíó¹ ÷è

b +

a

! 1 R

ðîçáiãà¹òüñÿ.

Геометричний змiст невласного iнтеграла площа вiдповiдно¨ безмежно¨ обла-

стi. Якщо площа скiнченна iнтеграл збiга¹ться i навпаки.

Приклад 1.

+1

b

dx

=

lim

dx

=

lim

(arctg b

¡

arctg 0) = ¼

:

1+x2

1+x2

0

b

+

0

b +

2

+R

! 1bR

! 1

Приклад 2.

1

dx

= b

lim

dx

=

lim (ln

1 + b

j ¡

ln 1) = +

1

:

0

1+x

0

b

+

1+x

+

j

R

! 1 R

! 1

Даний iнтеграл розбiжний.

118

Приклад 3.

x®

b

+

x® = b +

8

³

b

´¯

b

R

R

<

j

j

j

¯

+1

b

1

;

ïðè ® = 1;

1

1

® b®¡11

dx =

lim

dx

lim

:

(1¡®)x

¡

1

6

=

1 ;

ïðè ® > 1;

®1

1 ;

ïðè ® > 1;

8

³

1

´

! 1

1

! 1

8

(ln x )

1

;

¯

ïðè ® = 1

b +

¡

¡

b +

¡

ïðè

lim

:

®

=

lim

:1

® > 1

®

+1;

® · 1:

! 1

<

ln b;

R

ïðè ® = 1

! 1

<

Îòæå, ïðè

+1 dx

çáiæíèé, à ïðè

·

ðîçáiæíèé.

x

1

Аналогiчно визнача¹мо

b

b

Z

def

lim

f(x) dx;

f(x) dx =

a!¡1 Z

Z

¡1

a

Z

f(x) dx def= Z

f(x) dx +

f(x) dx:

+1

a

+1

¡1

¡1

a

Остання рiвнiсть означа¹, що iнтеграл злiва збiга¹ться, якщо збiгаються два iнтеграли справа.

18.2. Властивостi невласних iнтегралiв

Теорема 18.1. Нехай f; g : [a; +1) ! R двi функцi¨ такi, що 0 · f(x) · g(x)

для всякого x 2 [a; +1). Òîäi

+R

R

+

(à) ÿêùî

+1

g(x) dx çáiæíèé, òî i

+1

f(x) dx çáiæíèé;

a

a

R

R

(á) ÿêùî

1

f(x) dx ðîçáiæíèé, òî ðîçáiæíèé i

1

g(x) dx.

a

a

+

R

Приклад 4. Встановити, чи збiга¹ться iнтеграл

+1

dx

1

x2

(1+ex)

.

1

1

1 dx

Îñêiëüêè 0 ·

·

, à

x2

збiга¹ться, то збiга¹ться i наш iнтеграл.

x2(1+ex)

x2

1

R

+

R

+1 x+1

Приклад 5. Встановити, чи збiга¹ться iнтеграл

1

p

x3

dx.

iнтеграл.

R

1

x

x+1

1

1

Îñêiëüêè 0 < p

=

p

<

p

, à

p

dx ðîçáiãà¹òüñÿ, òî ðîçáiæíèé i íàø

x

x3

x3

1

x

+1

R

Теорема 18.2. Якщо збiга¹ться iнтеграл

+1

jf(x)j dx, то збiга¹ться також

a

iнтеграл

R

f(x) dx.

a

В цьому випадку iнтеграл +R1f(x) dx називають абсолютно збiжним.

a

119

Îñêiëüêè					+1				R
Приклад 6. Встановити, чи збiга¹ться iнтеграл									+1	sin x	dx.
									a	x2
çáiæíèé.					R
	j sin xj		1			1		збiжний, то наш iнтеграл абсолютно
		· x2 , а iнтеграл			a x2 dx
	x2

18.3. Iнтеграли вiд необмежених функцiй

Нехай f : [a; b) ! R неперервна функцiя, а в точцi b вона або невизначена, або ма¹ розрив.

Означення 18.2. Якщо iсну¹ границя

Zc Zb

lim	f(x) dx def= f(x) dx;

c!d¡0

aa

то вона назива¹ться невласним iнтегралом функцi¨ f ïî ïðîìiæêó [a; b).

¢

R

R

f : (a;¯ b]

ÿêà¡

â òî÷öi a

Приклад 7. 1

dx

b

dx

lim 2p

b

2p

2 = 2.

p

= lim

p

=

1

x

=

lim

1 b

0

1¡x

b!1¡0 0 1¡x

¡ b!1¡0

¡

¯

! R

¡ ¡

0

¡ b!1¡0

Аналогiчно визнача¹ться iнтеграл вiд функцi¨

àáî

невизначена, або ма¹ розрив.

18.4. Iнтеграли, залежнi вiд параметра

Розглянемо iнтеграл

Zb

I(®) = f(x; ®) dx;

a

який залежить вiд параметра ®. Нехай неперервна функцiя двох змiнних f визначена в областi f(x; y) 2 R2 j a · x · b; c · ® · dg i ма¹ неперервну похiдну по ®. Òîäi

Zb

I0(®) = f®0 (x; ®) dx:

(18.4.1)

a

Ця формула назива¹ться фомулою Лейбнiца. Нехай межi iнтегрування теж залежать вiд ®:

bZ(®)

I(®) =

f(x; ®) dx:

a(®)

									120
Òîäi	b(®)
I0(®) =	Z	f®0	(x; ®) dx + f (b(®); ®)	db		¡ f (a(®); ®)	da	:	(18.4.2)
				d®			d®
	a(®)
Приклад 8. Гама-функцiя
Розглянемо iнтеграл, який залежить вiд параметра ®
			+1
			Z
			x®¡1e¡x dx:						(18.4.3)
			0

Покажемо, що цей невласний iнтеграл iсну¹ при ® > 0. Зобразимо його у виглядi суми

+1	1	+1
Z0	x®¡1e¡x dx = Z0	x®¡1e¡x dx + Z1	x®¡1e¡x dx:

Перший iнтеграл збiга¹ться, так як

1	1
0 < Z	x®¡1e¡x dx < Z	x®¡1 dx =	1	:
			®

00

Другий iнтеграл теж збiжний. Нехай n 2 Z òàêå, ùî n > ® ¡ 1. Òîäi

+1		+1
0 < Z1	x®¡1e¡x dx <	Z1	xne¡x dx < +1:

Щоб обчислити останнiй iнтеграл, потрiбно взяти його n раз частинами i врахувати,

ùî lim xxn	= 0. Тобто ми означили деяку функцiю
x!1 e		Z0	xex dx:
	¡(®) =				(18.4.4)
		+1	®¡1

яку називають гама-функцi¹ю i часто використовують в застосуваннях математики.

+1	1			¡		¡x	¢¯¯	b
0					¡e
¡(1) =		dx =	lim						= 1:
Z	ex		b!+1					0

Нехай цiле число ® > 1.

¡(®) =

Z

xex

dx =

2 dv = e¡x dx

+1

®¡1

4

u = x®¡1

0

1

Z

xex

¡x®¡1e¡x 0

+ (® ¡ 1)

¯

+

+1

®¡2

0

¯

3

du = (® ¡ 1)x®¡2 dx 5 = v = ¡e¡x

dx = (® ¡ 1)¡(® ¡ 1):

Ми отримали рекурентну формулу

¡(®) = (® ¡ 1)¡(® ¡ 1):

(18.4.5)