matanaliz

61

Означення 7.5. Нехай f : A ! R i +1 (¡1) ¹ граничною точкою множини A. Пряма y = kx + b назива¹ться (похилою) асимптотою графiка функцi¨ f ïðè x ! +1 (x ! ¡1), ÿêùî

x!+1	¡		¡	b) = 0	µx!¡1 (f(x) ¡ kx ¡ b) = 0¶	:
lim (f(x)		kx			lim

З означення знаходимо

b = lim (f(x) ¡ kx)

x!§1

Îñêiëüêè

			lim (f(x)		lim		f(x)
							x ¡ k¶;
	µ		b = x!§1	¡ kx) = x!§1 x µ
òî lim		f(x)	= 0; i òîìó
x!§1		x ¡ k¶
			k = lim		f(x)	:
					x
				x!§1
Зокрема, якщо k = 0, то пряму y = b =						lim f(x) називають
						x!§1

тальною асимптотою.

7.4. Схема дослiдження графiкiв функцiй

(7.3.1)

(7.3.2)

горизон-

1.Знаходимо область визначення функцi¨, тобто область допустимих зна- чень виразiв, якi визначають функцiю; область значень (якщо це не вимага¹ додаткових дослiджень); нулi функцi¨, iнтервали знакосталостi; парнiсть, непарнiсть, перiодичнiсть.

2.Дослiджу¹мо функцiю на неперервнiсть, знаходимо асимптоти.

3.Знаходимо точки локальних екстремумiв, iнтервали монотонного зростання i спадання.

4.Знаходимо точки перегину та iнтервали опуклостi вниз i вверх.

5.Схематично буду¹мо графiк функцi¨.

62

7.5. Гiперболiчнi функцi¨

Як приклад, побуду¹мо графiки гiперболiчних функцiй. Функцi¨

	ch x def=	ex + e¡x	;	sh x def=	ex ¡ e¡x
		2			2

називаються вiдповiдно косинусом i синусом гiперболiчним. Будемо дослiджувати ¨х паралельно.

1. Область визначення цих функцiй вся дiйсна вiсь, оскiльки вони ¹ лiнiйною комбiнацi¹ю двох показникових функцiй. Функцiя ch парна, а функцiя

sh непарна. Такi функцi¨ можна дослiджувати тiльки з одного боку вiд нуля, а далi продовжувати за вiдповiдною симетрi¹ю. Функцiя ch всюди додатна, як сума додатних функцiй. Функцiя sh ì๠íóëü òiëüêè ïðè x = 0, вiд'¹мна лiворуч вiд нуля i додатна праворуч.

x	(1; 0)	0	(0; 1)
sh x	¡	0	+

2. Данi функцi¨ неперервнi скрiзь на областi свого визначення як лiнiйна комбiнацiя двох показникових функцiй. Асимптот вони не мають, оскiльки

	k = lim	ex § e¡x	=		1	= lim	ex ¨ e¡x	= +		:
		2x		n	1o		2		1
	x!+1					x!+1

3. Знайдемо похiднi.

= µ

x

¡ e¡

x

¶

0

e

x + e

¡

x

(ch x)0

e

=

= sh x;

2

2

= µ

x

+ e

¡

x

¶

0

e

x

¡ e¡

x

(sh x)0

e

=

= ch x:

2

2

Враховуючи данi попереднього пункту, робимо висновок, що функцiя sh всюди строго монотонно зроста¹, а функцiя ch âåäå ñåáå òàê:

x	(1; 0)	0	(0; 1)
(ch x)0	¡	0	+
ch x	#	min; ch(0) = 1	"

63

4. Другi похiднi вiд наших функцiй рiвнi ¨м самим. Тому функцiя ch всюди опукла вниз, а функцiя sh âåäå ñåáå òàê:

x	(1; 0)	0	(0; 1)
(sh x)00	¡	0	+
sh x	_	точка перегину, sh(0) = 0	^

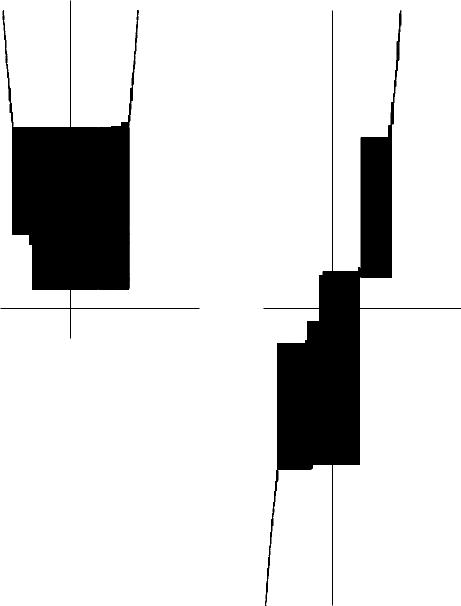
5. Враховуючи всi отриманi данi, буду¹мо графiк наших функцiй.

6	6

y = ch x

y = sh x

1q

-

1 q

-

q

Îñêiëüêè

x2

x3

xn

ex = 1 + x +

+

+ ¢ ¢ ¢ +

+ o(xn);

2!

3!

n!

e¡x = 1

x +

x2

x3

+

+ ( 1)n

xn

+ o(xn);

¡

¡

3!

¢ ¢ ¢

n!

2!

¡

64

то додаючи i вiднiмаючи цi формули i дiлячи на 2, отрима¹мо ще двi формули Маклорена:

6:

sh x = x +

x3

+

x5

+

x7

+ ¢ ¢ ¢ +

x2n¡1

+ o(x

2n

);

(7.5.1)

3!

5!

7!

(2n¡1)!

2

4

6

2n

7:

ch x = 1 +

x

+

x

+

x

+ ¢ ¢ ¢ +

x

+ o(x2n+1):

2!

4!

6!

(2n)!

Тепер пояснимо, звiдки взялась назва гiперболiчнi . Нагада¹мо, що коло x2 + y2 = 1 в параметричному виглядi зобража¹ться так:

x = cos t; y = sin t; t 2 [¡¼; ¼]:

Виявля¹ться, гiперболу x2 ¡y2 = 1 у параметричному виглядi можна зобразити так:

x = ch t; y = sh t:

Це справдi так, оскiльки ма¹ мiсце рiвнiсть:

x ¡ sh

x = ³e

´

¡ ³

ch2 x ¡ sh2 x = 1:

(7.5.2)

(ch

2

¡2

´

=

4

¡

e2x

¡ 4

= 1:)

2

2

x+e¡x

2

ex

e¡x

2

e2x+2+e¡2x

2+e¡2x

Тангенс i котангенс гiперболiчнi визначаються аналогiчно до звичайних:

th x def=

sh x

=

ex ¡ e¡x

;

cth x def=

ch x

=

ex + e¡x

:

ch x

ex + e¡x

sh x

ex ¡ e¡x

Знайдемо ¨х похiднi:

(th x)0 = µsh x¶0 ch x

(cth x)0 = µch x¶0 sh x

=		ch2 x ¡ sh2 x		=	1			;
		ch2 x				ch2 x
=	sh2 x ¡ ch2 x			=	1				:
		sh2 x			¡sh2 x

Тут ма¹мо повну аналогiю зi звичайними тангенсом i котангенсом. Спочатку побуду¹мо графiк функцi¨ y = th x.

1. Область визначення цi¹¨ функцi¨ вся дiйсна вiсь. Функцiя непарна i не перiодична. Функцiя th ì๠íóëü òiëüêè ïðè x = 0, вiд'¹мна лiворуч вiд нуля

i додатна праворуч.

x	(1; 0)	0	(0; 1)
th x	¡	0	+

65

2. Дана функцiя неперервна всюди як частка неперервних функцiй.

		ex ¡ e¡x					1 ¡	1			= 1;
	lim		=	lim				e2x
		ex + e¡x				1 +
x	+			x +	1				1
	! 1			!				e

i тому пряма y = 1 ¹ горизонтальною асимптотою при x ! +1, а з непарностi функцi¨ робимо висновок, що i пряма y = ¡1 ¹ горизонтальною асимптотою при

x ! ¡1.

3.

Îñêiëüêè (th x)0 =

1

> 0 всюди, то tg x всюди монотонно зроста¹.

2

x

ch

4.

Знайдемо другу похiдну:

(th x)00

=

1

= ¡2

sh x

:

ch

2

x

ch

3

x

Iнформацiю, яку вона да¹ про нашу функцiю подамо таблицею:

x	(1; 0)	0	(0; 1)
(th x)00	+	0	¡
th x	^	точка перегину; th(0) = 0	_

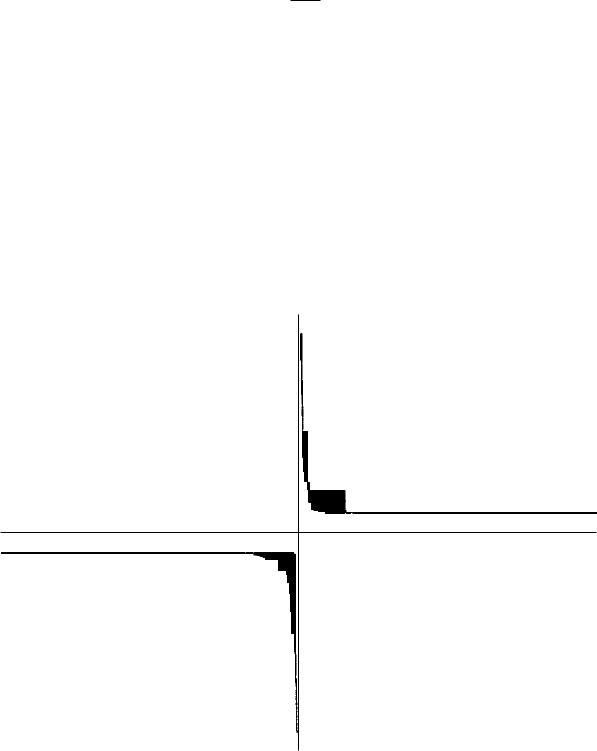
5. А ось графiк цi¹¨ функцi¨.

6
1 q	y = th x
	-
-1 q

Тепер побуду¹мо графiк функцi¨ y = cth x.

1. Область визначення цi¹¨ функцi¨ R n f0g. Функцiя непарна i не перiодична. Вкажемо iнтервали знакосталостi.

x	(1; 0)	0	(0; 1)
cth x	¡	@	+

66

2. Дана функцiя неперервна всюди на областi свого визначення як частка неперервних функцiй.

	ex + e¡x		1 +		1
lim		= lim			e2x		= 1;
			1 ¡			1
x!+1 ex ¡ e¡x		x!+1
						e2x

i тому пряма y = 1 ¹ горизонтальною асимптотою при x ! +1, i пряма y = ¡1 ¹ горизонтальною асимптотою при x ! ¡1.

lim

ex

+ e¡x

ex

+ e¡x

e

¡

x = +1;

xlim0 ex

e

x = ¡1;

x

!

+0 ex

¡

¡

!¡

¡

i пряма x = 0 ¹ вертикальною асимптотою.

3.Îñêiëüêè (cth x)0 = ¡sh12 x < 0 всюди на областi визначення, то ctg x всюди монотонно спада¹.

4.Знайдемо другу похiдну: µ 1 ¶0 ch x00

(cth x) =					= 2				:
		2	x			sh	3
ch								x

Iнформацiю, яку вона да¹ про нашу функцiю, подамо таблицею:

x	(1; 0)	0	(0; 1)
(cth x)00	¡	0	+
cth x	_	@	^

5. А ось графiк цi¹¨ функцi¨.

6

1 q	y = cth x
	-

-1 q

67

7.6. Функцiя Гауса

Функцi¹ю Гауса називають функцiю

'(x) = p12¼ e¡x22 :

1. Функцiя визначена на всiй дiйснiй осi i прийма¹ тiльки додатнi значення. Парна i неперiодична.

2.

Неперервна як суперпозицiя неперервних функцiй x òà

x2

¡ 2 . Îñêiëüêè

2

e

lim

p

1

e¡

x

= 0, то пряма y = 0 ¹ горизонтальною асимптотою.

2

2¼

x!+1

2

3.

'0(x) = ¡

p

x

e¡

x

, i '0(x) = 0 òiëüêè ïðè x = 0. Для додатних значень

2

2¼

x похiдна вiд'¹мна, а для вiд'¹мних додатна i тому функцiя строго монотонно зроста¹ при вiд'¹мних значеннях аргумента i спада¹ при додатних.

4. '00(x) =

p

1

e¡x22

¡x2 ¡ 1¢, i данi про поведiнку функцi¨ задамо табли-

öåþ.

2¼

x

(1; ¡1)

¡1

(-1,1)

1

(1; 1)

('(x))00

+

0

¡

0

+

'(x)

^

точка перегину,

_

точка перегину,

^

'(

1) =

p

1

'(1) =

p

1

¡

2¼e

2¼e

5. Тепер все отримане вiдобразимо на графiку.

1

6

x2

q

'(x) =

p

1

e¡

2

-

2¼

Або трохи збiльшимо масштаб:

6

p1

r 2¼

r

-1q

r
1q	-

Частина 3

Функцi¨ багатьох змiнних

m-âèìiðíèì åâêëi-

69

ÐÎÇÄIË 8

ПОНЯТТЯ ПРО ФУНКЦIˆ БАГАТЬОХ ЗМIННИХ

1. m-вимiрний евклiдовий простiр.

2.Пiдмножини евклiдового простору Rm.

3.Функцi¨ вiд m çìiííèõ.

4.Послiдовностi точок простору Rm.

5.Границя та неперервнiсть функцiй m çìiííèõ.

8.1. m-вимiрний евклiдовий простiр

Означення 8.1. Назвемо m-âèìiðíèì координатним простором Am ìíî- жину всеможливих впорядкованих послiдовностей m дiйсних чисел

Am := f(x1; x2; : : : ; xm) j x1; x; : : : ; xm 2 Rg:

Всяку таку послiдовнiсть (x1; x2; : : : ; xm) називемо точкою координатного про-

стору	Am i, залежно вiд ситуацi¨, будемо позначати рiзними	способами: або
(x1; x2	; : : : ; xm), àáî M(x1; x2; : : : ; xm) (чита¹ться: точка M	з координатами
(x1; x2	; : : : ; xm)), або просто через M.
Задамо дi¨ над точками простору Am:

1. додавання: (x1; x2; : : : ; xm) + (y1; y2; : : : ; ym) := (x1 + y1; x2 + y2; : : : ; xm + ym), для всяких (x1; x2; : : : ; xm); (y1; y2; : : : ; ym) 2 Am;

2. множення на скаляр: ¸ ¢ (x1; x2; : : : ; xm) := (¸ ¢ x1; ¸ ¢ x2; : : : ; ¸ ¢ xm),

для всякого (x1; x2; : : : ; xm) 2 Am i ¸ 2 R.

Простiр Am з цими операцiями перетворю¹ться на лiнiйний векторний простiр, i такi простори вивчаються в курсi лiнiйно¨ алгебри. Додатково означимо вiддаль мiж

точками простору Am:
								(8.1.1)
2		x		y	)2	2
d(M; N) = p(x1 ¡ y1) + (m2.			¡	2		+ ¢ ¢ ¢ + (xm ¡ ym)	;
äå M(x1; x2; : : : ; xm); N(y1; y2; : : : ; ym) 2 A

Означення 8.2. Координатний простiр Am з операцiями додавання та множен- ня на скаляр та вiддаллю, заданою рiвнiстю (8.1.1) назива¹ться

довим простором i познача¹ться як Rm.

70

Òàê, R2 def= f(x; y) j x; y 2 Rg. Для всяких M1(x1; y1); M2(x2; y2) 2 R2 ìà¹ìî

d(M1; M2) = p					:
				(x1 ¡ x2)2 + (y1 ¡ y2)2			ìà¹ìî
R3 def= f(x; y; z) j x; y; z 2 Rg. Для всяких M1(x1; y1; z1); M2(x2; y2; z2) 2 R3
d(M1; M2) = p						:
		(x1 ¡ x2)2 + (y1 ¡ y2)2 + (z1 ¡ z2)2
Äëÿ R = R1 d(M1; M2) = p			= jx1 ¡ x2j.
	(x1 ¡ x2)2
8.2. Пiдмножини евклiдового простору Rm

Означення 8.3. Нехай M(x1; x2; : : : ; xm) 2 Rm довiльна точка i r > 0

довiльне число. Множина:						< rg назива¹ться вiдкритою кулею ðàäióñà
B(M; r)	def=	fP	2 Rm j d(M; P )				r ç
центром в точцi M;
¹	def=	fP	2 R	m	j d(M; P )	· rg назива¹ться замкненою кулею ðàäióñà	r ç
B(M; r)

центром в точцi M;

S(M; r) def= fP 2 Rm j d(M; P ) = rg назива¹ться сферою ðàäióñà r з центром в точцi

M.

Означення 8.4. "-околом точки M 2 Rm назвемо множину B(M; ").

Означення 8.5. Нехай A ½ Rm деяка множина. Точка M 2 A назива¹ться

внутрiшньою точкою множини A, якщо вона належить множинi разом з деяким

ñâî¨ì "-околом.

Точка M назива¹ться зовнiшньою точкою множини A, якщо вона ¹ внутрi-

шньою точкою множини ¹	m	n A.
A = R

Точка M назива¹ться точкою ìåæi множини A, якщо вона не ¹ нi внутрiшньою, нi зовнiшньою.

Означення 8.6. Множина назива¹ться вiдкритою, якщо всi ¨¨ точки внутрiшнi, множина назива¹ться замкненою, якщо ¨¨ доповнення множина вiдкрита.

Означення 8.7. Неперервною кривою L в просторi Rm назвемо множину

L = f(x1; x2; : : : ; xm) 2 Rm j x1 = '1(t); x2 = '2(t); : : : ; xm = 'm(t); t 2 [0; 1]; g

äå âñi 'i, i = 1; : : : ; m неперервнi функцi¨. Кажемо, що крива L ç'¹äíó¹ точки

M1('1(0); '2(0); : : : ; 'm(0)) òà M2('1(1); '2(1); : : : ; 'm(1)).