Математика для економістів Ден.. 2010 ч

Рівняння лінії у просторі Як на площині, так і в просторі будь-яка лінія може бути визначена як

сукупність точок, координати який в деякій обраній в просторі системі координат задовольняють рівнянню:

F(x, y, z) = 0.

Це рівняння називається рівнянням лінії в просторі. Крім того, лінія в просторі може бути визначена і інакше. Її можна розглядати як лінію перетину двох поверхонь, кожна з яких задана яким-небудь рівнянням.

Нехай F(x, y, z) = 0 і Ф(x, y, z) = 0 – рівняння поверхонь, які перетинаються по лінії L.

Тоді пару рівнянь

F (x, y, z) 0 Ф(x, y, z) 0

назвемо рівнянням лінії в просторі.

Рівняння прямої в просторі по точці і напрямному вектору

Візьмемо довільну прямую і вектор S (m, n, p), паралельний заданій прямій.

Вектор S називається напрямним вектором прямої.
На прямій візьмемо дві довільні точки М0(x0, y0, z0) і M(x, y, z).
		z
			S		M1
		M0
		r0	r
		0			y
	x
Позначимо радіус-вектори цих точок як r					і r , очевидно, що
			0
		r - r	= М	0	М .
		0
Так як вектори	М 0 М і S	колінеарні, то вірно співвідношення

М 0 М = S t,

де t – деякий параметр.

r = r

Отже, можна записати:

+ S t.

0

Так як цьому рівнянню задовольняють координати будь-якої точки прямої, то

отримане рівняння – параметричне рівняння прямої.

Це векторне рівняння може бути записано в координатній формі:

x

x0

mt

y

y0

nt

z

z0

pt

Цю систему рівнянь можна записати у вигляді:

x x0

y

y0

z

z0

- канонічне рівняння прямої у просторі.

m

n

p

Означення. Напрямними косинусами прямої називаються напрямні косинуси

вектора S , які можуть бути обчислені за формулами:

cos

m

; cos

n

;

cos

p

.

m2

n2

p 2

m2

n2

p 2

m2

n2 p 2

Звідки отримаємо: m : n : p = cos

: cos

: cos .

Числа m, n,

p

називаються кутовими

коефіцієнтами

прямої. Так як

S -

ненульовий вектор, то m, n і p не можуть дорівнювати нулю одночасно, але одне або два з цих чисел можуть дорівнювати нулю. В цьому випадку в рівнянні прямої необхідно прирівняти до нуля відповідні чисельники.

Рівняння прямої у просторі, яка проходить через дві задані точки

Якщо на прямій відмітити дві довільні точки M1(x1, y1, z1) і M2(x2, y2, z2), то координати цих точок мають задовольняти рівнянню прямої:

x2 x1		y2 y1		z2 z1	.
m		n		p

Крім того, для точки М1 можна записати:

x x1		y y1		z z1	.
m		n		p

Розв‟язуючи сумісно ці рівняння, отримаємо:

x		x1		y		y1		z		z1	.
x	2	x		y	2	y		z	2	z
		1				1				1

Це рівняння прямої, яка проходить через дві точки у просторі.

Загальне рівняння прямої у просторі

Рівняння прямої може бути розглянуто як рівняння лінії перетину двох

площин.

Як було розглянуто вище, площина у векторній формі може бути задана

рівнянням:

	r + D = 0,
N

де N - нормаль площини; r - радіус-вектор довільної точки площини.
Нехай в просторі задані дві площини: N1 r +D1=0 і N 2					r +D2=0, вектори
нормалі мають координати: N1 (A1,B1,C1), N 2 (A2,B2,C2); r (x,y,z).
Тоді загальні рівняння прямої в векторній формі:
N1	r	D1	0	.
N 2	r	D2	0

Загальні рівняння прямої в координатній формі:

A1 x B1 y C1 z D1	0
A2 x B2 y C2 z D2	0 .

Практична задача часто полягає у зведенні рівнянь прямих в загальному вигляді до канонічному виду.

Для цього потрібно знайти довільну точку прямої і числа m, n, p. При цьому напрямний вектор прямої може бути обчислений як векторний добуток векторів нормалі до заданих площин.

i

j

k

B

C

A

C

A

B

S N1 N2

A1

B1

C1

i

1

1

j

1

1

k

1

1

i m jn kp.

B2

C2

A2

C2

A2

B2

A2

B2

C2

Кут між площинами

Кут між площинами в просторі

пов‟язаний з кутом між нормалями до цих

площин

1 співвідношенням:

=

1 або

=1800-

1, тобто cos

= cos 1.

N 2

1

0

N1

Визначимо

кут

1.

Відомо,

що

площини

можуть

бути задані

співвідношеннями:

N1

r

D1

0

,

N 2

r

D2

0

де N1 (A1, B1, C1),

N 2

(A2, B2,

C2). Кут

між

векторами

нормалі

знайдемо з їх

скалярного добутку:

cos

N1

N 2

.

1

N1

N 2

Таким чином, кут між площинами знаходиться за формулою:

cos

A1 A2

B1 B2

C1C2

.

A2

B 2

C 2

A2

B 2

C 2

1

1

1

2

2

2

Умова паралельності і перпендикулярності площин

Для того, щоб площини були перпендикулярні необхідно і достатньо, щоб

косинус кута між площинами дорівнював нулю. Ця умова виконується, якщо:

						A1 A2	B1 B2		C1C2 0 .
Площини паралельні, якщо вектори нормалей колінеарні: N1 N 2 .Ця умова
виконується, якщо:	A1		B1		C1	.
	A2		B2		C2
				Кут між прямими в просторі
Нехай в просторі задані дві прямі. Їх параметричні рівняння:
						l1:
							r	r1	S1t
						l2:
							r	r2	S2t

r (x, y, z); r1	(x1 , y1 , z1 ); r2	(x2 , y2 , z2 ); S1 (m1 , n1 , p1 ); S2	(m2 , n2 , p2 ).

Кут між прямими

і кут між напрямними векторами

цих прямих

пов‟язані співвідношеннями:

= 1 або

=1800 - 1. Кут між напрямними

векторами знаходиться із скалярного добутку. Таким чином:

cos

S1 S2

m1m2

n1n2

p1 p2

.

S

1

S

2

m2

n2

p 2

m2

n2

p 2

1

1

1

2

2

2

Умови паралельності і перпендикулярності прямих в просторі Щоб дві прямі були паралельні необхідно і достатньо, щоб напрямні вектори

цих прямих були колінеарні, тобто їх відповідні координати були пропорційні:

m1		n1		p1	.
m2		n2		p2

Щоб дві прямі були перпендикулярні необхідно і достатньо, щоб напрямні вектори цих прямих були перпендикулярні, тобто косинус кута між ними дорівнює нулю:

m1m2 n1n2	p1 p2	0 .
Кут між прямою і площиною
Означення. Кутом між прямою і площиною називається будь-який кут між
прямою і її проекцією на цю площину.
Нехай площина задана рівнянням	N r	D 0 , а	пряма -	r r0	St . З
геометричних міркувань (див. рис.) видно, що шуканий кут			= 900 -	, де	- кут

між векторами	N	і S .
				N	S

Цей кут може бути обчисленим за формулою:

N

S

,

cos

N

S

N

S

sin

cos

.

N

S

В координатній формі: sin

Am

Bn

Cp

.

A2

B 2

C 2

m2

n2 p 2

Умова паралельності і перпендикулярності прямої і площини у просторі Для того, щоб пряма і площина були паралельні, необхідно і достатньо, щоб

вектор нормалі до площини і напрямний вектор прямої були перпендикулярні. Для цього необхідно, щоб їх скалярний добуток дорівнював нулю:

N S,	N S 0, sin 0, Am Bn Cp 0.

Для того, щоб пряма і площина були перпендикулярні, необхідно і достатньо,

щоб вектор нормалі до площини і напрямний вектор прямої були колінеарними. Ця умова виконується, якщо векторний добуток цих векторів дорівнював нулю:

N	S 0;	A		B		C .
		m		n		p

Приклади

1. Знайти рівняння площини, яка проходить через дві точки P(2; 0; -1) і Q(1; - 1; 3) перпендикулярно площині 3х + 2у – z + 5 = 0.

Розв'язок. Вектор нормалі до площини 3х+2у–z+5=0 N (3;2; 1) паралельний до шуканої площини.

Отримаємо:

	x	2	y	0	z		1
	1	2	1	0	3		1		0
		3	2		1
	x	2	y	z	1
		1	1	4			0
		3	2	1
(x		2)(1		8) y(1			12)			(z 1)( 2 3) 0
	7(x		2)	11y		(z			1)	0
	7x		14	11y		z	1			0
	7x		11y	z	15		0

2. Знайти рівняння площини, яка проходить через точки А(2, -1, 4) і В(3, 2, -1)

перпендикулярно площині х+у +2z–3 = 0.

Розв'язок. Шукане рівняння площини має вигляд: Ax+By+Cz +D = 0, вектор нормалі до цієї площини n1 (A, B, C). Вектор AB (1, 3, -5) належить площині. Задана нам площина, перпендикулярна шуканій має вектор нормалі n2 (1, 1, 2). Так як точки А і В належать обом площинам, а площини взаємно перпендикулярні, отже

	i	j	k			3	5				1	5				1	3
n1 AB n2	1	3	5	i		1	2		j		1	2		k		1	1		11i 7 j 2k.
	1	1	2

Таким чином, вектор нормалі n1 (11, -7, -2). Так як точка А належить шуканій площині, то її координати мають задовольняти рівнянню цієї площини, тобто: 11 2

+ 7 1 - 2 4 + D = 0; D = -21.

Отже, отримаємо рівняння площини: 11x - 7y – 2z – 21 = 0.

3. Знайти рівняння площини, знаючи, що точка Р(4; -3; 12) – основа

перпендикуляра, опущеного з початку координат на цю площину.

Розв'язок.

OP		(4;		3;12);					OP	16 9 144 169 13
N	(	4	;		3	;	12	)
		13		13 13

Таким чином, A = 4/13; B = -3/13; C =12/13, скористаємося формулою:

A(x – x0) + B(y – y0) + C(z – z0) = 0.

134 (x 4) 133 ( y 3) 1213 (z 12) 0

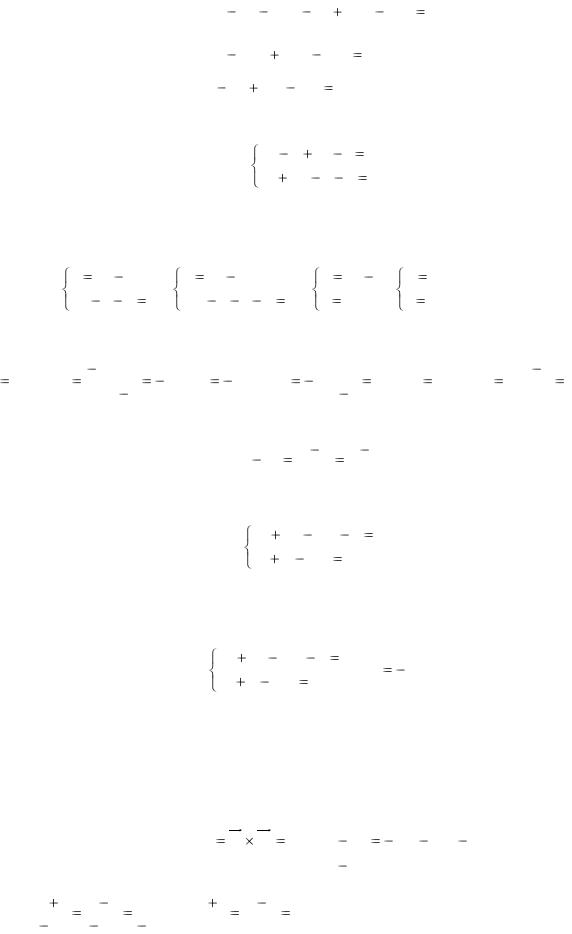
4		x	16				3				y		9				12		z	144		0
13			13				13						13			13				13
4		x	3			y			12			z	169						0
13			13				13						13
4x			3y			12z					169					0.

4. Знайти канонічне рівняння, якщо пряма задана у вигляді:

2x	y	3z	1	0 .
5x	4 y	z	7	0

Розв'язок. Для знаходження довільної точки прямої, припустимо що її координата х

= 0, а потім підставимо це рівняння в задану систему рівнянь:

y

3z

1

y

3z 1

y

3z

1

y 2

, тобто А(0, 2, 1).

4 y z 7 0 12z 4 z 7 0 z 1

z 1

Знаходимо координати напрямного вектора прямої.

m

B1

C1

11;

n

A1

C1

2 3

17;

p

A1

B1

2 1

13.

1 3

B2

C2

4

1

A2

C2

5

1

A2

B2

5 4

Отримаємо канонічне рівняння прямої:

x

y 2

z

1

.

11

17

13

5. Привести до канонічного виду рівняння прямої, задане у вигляді:

2x

3y

16z

7

0 .

3x

y

17z

0

Розв'язок. Для знаходження довільної точки прямої, яка є лінією перетину заданих площин, покладемо z = 0. Тоді:

2x 3y 16z 7 0; y

3x ;

3x y 17z

0

2x – 9x – 7 = 0;

x = -1; y = 3.

Отримаємо: A(-1; 3; 0).

i

j

k

Напрямний вектор прямої: S

n1

n2

2

3

16

35i

14 j

7k .

3

1

17

Отже:

x 1

y 3

z

;

x

1

y 3

z

.

35

14

7

5

2

1

6. Подані координати вершин трикутника АВС: А (3,3,9), В (2,3,5), С(4,7,5).

Знайти:

а) довжину та рівняння медіани ВЕ;

б) довжину висоти ВД;

в) внутрішній кут А у радіанах з точністю до 0,01;

г) площу трикутника;

д) рівняння прямої , яка проходить через т. Е паралельно прямій ВС.

Розв'язок. Знайдемо координату точки Е

	X							X A							X C					; Y							YA								YC			; Z										Z A						ZC			;
		E																																										E
													2									E					2																										2
	X E						3						4		3,5						;	YE					3							7					5 ;					Z E			9						5			7 .
							2																				2																				2
Рівняння медіани знайдемо за формулою
	X						X B										Y				YB							Z							Z B					,
	X E							X B							YE						YB						Z E									Z B
	x 2										y				3					z		5			– рівняння медіани BE.
	1,5												2								2
Довжину медіани ВЕ знаходимо за формулою
										X E								2					YE				2									Z E								Z B			2
	BE															X B											YB
															2 2							3 2												5 2
	BE						3,5														5						7																	10,25
Координати векторів АВ і АС знаходимо за формулами
	AB = (2-3; 3-3; 5-9) = (-1; 0; -4),																																										AC = (4-3; 7-3; 5-9) = (1; 4; -4).
Внутрішній кут А у радіанах знаходимо за формулою
cos									AB AC /											AB		*			AC
1 ( 1) 0 4 ( 4) ( 4) / ( 1)2																																							02					( 4)2 * 12												42		( 4)2
																																																												15/ 17 * 33
Векторний добуток векторів AB і AC знаходимо за формулою:
													i					j					k
	AB * AC												1 0									4							4k 4 j 16i 4 j 16i 8 j 4k
													1					4				4
																																														1															1
																																															162									8)2		( 4)2
Знайдемо площу трикутника АВС: S																																																					(									336					кв. од.
																																												2																2

В

А Д E С

Довжину сторони АС знаходимо за формулою:

	AC						12					42				4 2						1		16	16	33 .
Знайдемо довжину висоти ВД
S					1		AC				*				BД				,
				2
1									1
		336													33 *					ДВ	,
2									2
	ДВ						336 /									33

Знайдемо рівняння прямої, яка проходить через точку Е ( 3,5;5;7;) паралельно прямій сторони ВС.

Рівняння ВС знайдемо за формулою																	X	X B		Y	YB		Z	ZB	,
																	X C	X B	YC		YB		ZC	ZB
	x	2		y	3		z	5	,	x	2		y 3		z 5	– рівняння прямої ВС.
4		x	7		3	5		5			2	4		0

Рівняння прямої, яка проходить через точку Е паралельно прямій ВС знаходимо за формулою

X

X E

Y

YE

Z

ZE

,

2

4

0

X

3,5

Y

5

Z

7

.

2

4

0

Завдання

1. Записати рівняння прямої, яка проходить через точку M і має напрямний

:

вектор a

В. 1

M ( -1; 2; 5) ;

(2;1;6)

В. 2

(7;1;4)

a

M ( -4; 2; 6) ; a

В. 3

M ( 1; -4; 0) ;

(4;-1;5)

В. 4

(-2;3;6)

a

M ( 1; -3; 5) ; a

В. 5

M (-5; 2; 3) ;

(-2;3;8)

В. 6

(5;-1;3)

a

M ( 1; 0; -7) ; a

	2. Визначити відстань від точки Р до площини АВС :
В. 1	(АВС) :	3x + 4y – 5z + 2 = 0 ;	P ( 10; 8; 1 ).
В. 2	(АВС) :	– 2x + y – 3z –1= 0 ;	P ( -7; 6; 5 ).