Математика для економістів Ден.. 2010 ч

x2 – 6x + 8 = 0;

x2 – 8x + 12 = 0;

D = 36 – 32 = 4;

D = 64 – 48 = 16;

x1 = (6 + 2)/2 = 4;

x1 = (8 + 4)/2 = 6;

x2 = (6 – 2)/2 = 2 ;

x2 = (8 – 4)/2 = 2;

Тоді lim

(x

2)(x

4)

lim

x

4

2

1

.

(x

2)(x

6)

x

6

4

2

x 2

x 2

10. Знайти границю: lim

1

x x 2

1 x x 2

.

2

x 0

x

x

Розв'язок. Помножимо чисельник і знаменник дробу на спряжений вираз:

			lim					1	x		x2	1	x	x2										lim								2x								=
			x	0 x(x				1)(	1		x	x2		1 x				x2 )						x	0 x(x				1)(	1 x			x2		1 x x2 )
		2			1.
1		(1	1)
			11. Знайти границю: lim													x2			5x				6	.
																	x	2		9
													x	3
Розв'язок.
lim		x 2		5x 6				x 2			5x	6	(x	2)(x						3)				lim			(x		2)(x	3)			3	2			1	.
			x 2	9																							(x		3)(x	3)		3		3	6
	x 3																							x	3
			12. Знайти границю: lim												x3					6x2				11x			6	.
																	x			2			3x		2
													x	1

Розв'язок. Розкладемо чисельник і знаменник на множники: x2 – 3x + 2 = (x – 1)(x – 2)

x3 – 6x2 + 11x – 6 = (x – 1)(x – 2)(x – 3), так як

	x3 – 6x2 + 11x – 6		x - 1
x3 – x2	x2 – 5x +
		6

-5x2 + 11x

-5x2 + 5x

6x - 6

6x - 6

				0
	x2 – 5x + 6 = (x – 2)(x – 3);
	Тоді lim	(x 1)(x 2)(x 3)		2 .
		(x 1)(x 2)
	x 1

Завдання

Знайти границі функції:

В. 1

1.	lim												x						4						;
								3
													x						24
	x	3
2.	lim								2x 2											x		6								;
									x		2							8x				12
	x	2
3.	lim									3x									1			2						;
											1								x	3
	x	1
4.	lim								x3										x			1						.
														x		3				1
	x
		В. 3
1.	lim									3x										4				;
									3
											28										x
	x	1
										x				2					x			12
2.	lim																														;
									2x						2				7x									3
	x	3
3.	lim												x						9			3						;
																	x		2
	x	0
4.	lim										5x2										3x										1	.
														1					x								x		2
	x
		В. 5
															2
										x									1									2
1.	lim																													;
															3
																	9 x
	x	1
2.	lim								x2										2x									8			;
													x			2				4x
	x	4
3.	lim										11								x			3									;
											x				2				3x									2
	x	2
4.	lim								2x6											x								2			.
															x			2		3
	x

В. 2

1. lim 2sin									x				3cos			2	x		tgx	;
								2									4
	x
					2
2.	lim				x		3x					4			;
					2				5x 3
	x	1			2x
3.	lim					2x		1				3	;
						x	4
	x	4
4.	lim				2x 2				x			3		.
					3
	x					x		4
						В. 4
		1.				lim						8x3			4x		5		;
													x		2
						x	0								x
												2
		2.				lim						x			8x		9		;
												2			10x		9
						x		9				x

3.lim 11 x x 2 2 ;

x1

4.	lim					3x 2						5			.
							x	3				1
	x
						В. 6
		3				2
1.	lim						x					26					;
							2					2
	x	5					x
2.	lim				x3					4x2										4x		;
									x			3					8
	x	2
3.	lim				2						x						8		;
									1
	x	4				2								x
											2
		4.					lim							3x7							2	.
															3					x	7
							x

Питання для самоконтролю

13.Що називається функцією? Навести приклади.

14.Що називається областю визначення та множиною значень функції?

15.Охарактеризувати основні способи задання функції.

16.Які функції називаються основними елементарними функціями?

17.Яка функція називається складеною ? Навести приклади.

18.Яка функція називається елементарною?

19.Що називається числовою послідовністю?

20.Що називається границею числової послідовності?

21.Що називається границею функції в точці?

22.Які функції називаються нескінчено малими?

23.Які функції називаються нескінчено великими?

24.Ознаки існування границі послідовності.

Література [1,2,4]

ПРАКТИЧНЕ ЗАНЯТТЯ №10, 11

Тема 6. Диференціальне числення функції однієї змінної

Мета заняття. Вивчення теми надасть студентам можливість знати поняття функції однієї змінної, означення похідної, диференціала, їх геометричний зміст. Набути навички обчислення похідної складної, оберненої та заданої неявно функцій. Ознайомитись з правилом Лопіталя для обчислення границь.

План заняття

1.Функція однієї змінної. Означення похідної.

2.Похідна елементарних функцій.

3.Диференціал. Геометричний зміст похідної і диференціала.

4.Похідна складної, оберненої та заданої неявно заданої функцій.

5.Правило Лопіталя для обчислення границь.

Методичні рекомендації до практичного заняття

Означення. Нехай X і Y – деякі числові множини і нехай кожному елементу x X за деякому закону f поставлено у відповідність лише один елемент y Y .

Тоді визначена функціональна залежність y від x за законом y f (x) . При цьому x називають незалежною змінною ( або аргументом), y - залежною змінною,

множина X – областю визначення (існування) функції, множина Y – областю значень (зміни) функції.

Задати функцію - означає, вказати закон f визначення залежної змінної для

кожного значення аргументу із області визначення функції.

Означення. Основними елементарними функціями називаються такі функції:

степенева, показникові, логарифмічна, тригонометрична і обернені тригонометричні функції.

Означення. Елементарною функцією називається функція, яка утворюється за допомогою скінченої кількості арифметичних дій і суперпозицій основних

елементарних функцій.

Означення. Похідною функції f(x) в точці х = х0 називається границя відношення приросту функції в цій точці до приросту аргументу, якщо він існує:

f (x)	lim	f (x	x)	f (x)
			x
	x 0
у
			f(x)
f(x0 + x)			P
f
f(x0)	M
	x
0	x0	x0 +	x		x

	Нехай f(x) визначена на деякому проміжку (a, b). Тоді tg	f	тангенс кута
		x

нахилу січної МР до графіку функції.

	lim tg	lim	f	f (x0 ) tg	,
			x
	x 0	x 0

де - кут нахилу дотичної до графіку функції f(x) в точці (x0, f(x0)).

Кут між кривими може бути визначений як кут між дотичними, проведеними

до цих кривих в будь-якій точці.
Рівняння дотичної до кривої: y	y0 f			(x0 )(x		x0 )
Рівняння нормалі до кривої: y	y0			1	(x	x0 ) .
			f	(x0 )

Фізичний зміст похідної функції f(t), де t- час, а f(t)- закон руху (зміни координат) – миттєва швидкість руху.

Відповідно, друга похідна функції – швидкість зміни швидкості, тобто прискорення.

Односторонні похідні функції в точці

Означення. Правою (лівою) похідною функції f(x) в точці х = х0 називається

	праве (ліве) значення границі відношення					f	при умові, що це співвідношення
						x
	існує.
	f (x		) lim	f			f (x		) lim	f	.
		0						0
			x 0	x					x 0	x

Якщо функція f(x) має похідну в деякій х = х0, то вона має в цій точці односторонні похідні. Однак, обернене твердження невірне. По-перше функція може мати розрив в точці х0, а по-друге, навіть якщо функція неперервна в точці х0,

вона може бути в ній не диференційованою.

Наприклад: f(x)= x - має в точці х=0 і ліву і праву похідну, неперервна в цій точці,

однак, не має в ній похідної.

Теорема. (Необхідна умова існування похідної). Якщо функція f(x) має

похідну в точці х0, то вона неперервна в цій точці.

				Ця умова не є достатньою.
						Основні правила диференціювання
				Позначимо f(x) = u, g(x) = v- функції, диференційовані в точці х.
1)	(u			v) = u		v ;
2)	(u v) = u v + u v;
3)		u			u v v u	, якщо v 0 ;
		v			v2

Похідні основних елементарних функцій

	1) С						= 0;									9)		sin x	cos x
2) (xm)						= mxm-1;										10)		cos x			sin x
3)							1									11)		tgx	1
			x
																			cos2 x
								2 x
		1							1							12)		ctgx	1
4)
																				sin						2	x
		x							x 2
5)			e x					e x								13)	arcsin x									1
																			1									x 2
6)	a x						a x ln a									14)	arccosx										1
																								1 x 2
7)		ln x					1									15)		arctgx	1
										x									1							x2
8)	loga x						1									16)	arcctgx										1
									x ln a										1									x2

Похідна складної функції

Теорема. Нехай y = f(x); u = g(x), причому область значень функції u входить

в область визначення функції f.

Тоді

y

f (u)

u .

Логарифмічне диференціювання

ln x, при x

0

Розглянемо функцію y

ln

x

ln(

x),

при

x

0 .

Тоді (ln x ) =

1

, так як

ln x

1

;

(ln(

x))

(

x)

1

.

х

x

x

x

Враховуючи отриманий результат, можна записати:

f (x)

.

ln

f (x)

f (x)

f (x)

Відношення

називається логарифмічною похідною функції f(x).

f (x)

Метод логарифмічного диференціювання полягає в тому, що спочатку знаходять логарифмічну похідну функції, а потім похідну самої функції за формулою:

g(x)

f (x) (ln f (x) ) f (x) .

Похідна показниково-степеневої функції

Функція називається показниковою, якщо незалежна змінна входить в показник степеня, і степеневою, якщо змінна є основою. Якщо ж і основа і показник степеня залежать від змінної, то така функція буде показноково-

степеневою.

Нехай u=f(x) и v=g(x) – функції, які мають похідні в точці х, f(x)>0.

Знайдемо похідну функції y=uv. Логарифмуючи, отримаємо:

lny = vlnu

		y	v ln u			v	u
		y					u
	y		u v v	u		v ln u
				u
	Звідки отримаємо:
	u v		vuv 1u u v v ln u .

Похідна обернених функцій

Нехай необхідно знайти похідну функції у = f(x) за умови, що обернена їй функція x = g(y) має похідну, відмінну від нуля у відповідній точці.

Для рішення цієї задачі диференціюємо функцію x по x :

1 g ( y) y ;

Так як g (y) 0	y	1			;
		g ( y)
			dy		1				,
			dx				dx
							dy

тобто похідна оберненої функції обернена по величині похідної даній функції.

Наприклад. Знайти формулу для похідної функції arctg.

Функція arctg є функцією, оберненою до функції tg, тобто її похідна може бути знайдена наступним чином:

y tgx;

x arctgy;

Відомо, що y (tgx)	1	;
	cos2 x

По наведеній вище формулі отримаємо:

			y	1	;	d (arctgy)			1		.
				d (arctgy) / dx			dy			1/ cos2 x
Так як	1		1 tg 2 x 1	y 2 ; то можна записати кінцеву формулу для похідної
	cos2
		x
арктангенса:
				(arctgy)		1		.
							1 y 2

Таким чином отримані всі формули для похідних арксинуса, арккосинуса і

інших обернених функцій, наведених в таблиці похідних.

Диференціал функції

Нехай функція y= f(x) має похідну в точці х:

lim

y

f (x) .

x

x 0

Тоді можна записати:

y

f

(x)

, де

0, при х 0.

x

Отже:

y

f (x)

x

x .

Величина

x - нескінченно мала більш

високого порядку, ніж f (x) x, тобто

f (x) x- головна частина приросту

у.

Означення. Диференціалом функції f(x) в точці х називається головна

лінійна частина приросту функції.

Позначається dy або df(x).

Із означення слідує, що dy = f (x)

x

або

dy = f (x)dx.

Можна також записати:

f

(x)

dy

.

dx

Геометричний зміст диференціалу

y

f(x)

K

dy

M y

L

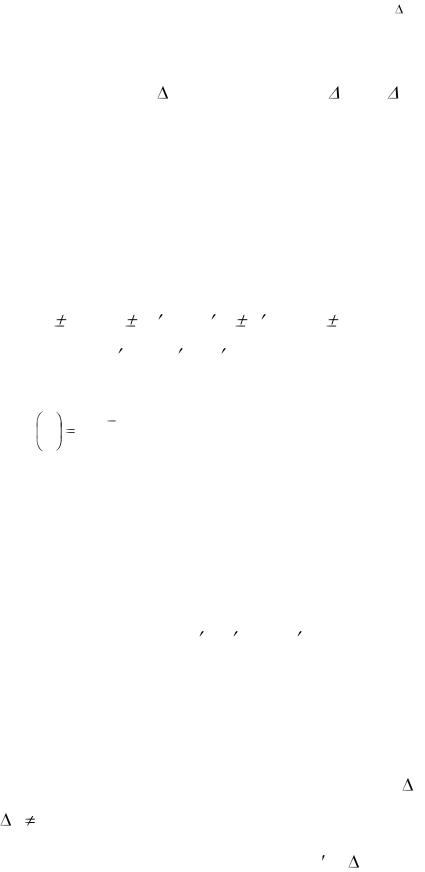
x

x + x

x

З трикутника MKL: KL = dy = tg x = y x.

Таким чином, диференціал функції f(x) в точці х дорівнює приросту ординати дотичної до графіка цієї функції в розглядаємій точці.

Властивості диференціала

Якщо u = f(x) і v = g(x)- функції, диференційовані в точці х, то безпосередньо із означення диференціала слідують наступні властивості:

1) d(u v) = (u v) dx = u dx v dx = du dv

2)d(uv) = (uv) dx = (u v + v u)dx = vdu + udv

3)d(Cu) = Cdu

4) d	u		vdu udv
	v		v2

Диференціал складної функції

Інваріантна форма запису диференціалу

Нехай y = f(x), x = g(t), тобто у - складна функція.

Тоді	dy = f (x)g (t)dt = f (x)dx.

Форма запису диференціала dy не залежить від того, чи буде х незалежною змінною або функцією будь-якої іншої змінної, у зв‟язку з чим ця форма запису називається інваріантною формою запису диференціала.

Однак, якщо х - незалежна змінна, то dx = x, але якщо х залежить від t, то

хdx.

Таким чином, форма запису dy = f (x) x не є інваріантною.

Розкриття невизначеностей

Правило Лопіталя.

(Лопіталь (1661-1704) – французький математик)

До невизначеностей відносять наступні співвідношення:

0	;		; 0; 0 ; 1 ;	.
0

Теорема (правило Лопіталя). Якщо функції f(x) і g(x) диференційовані в околі точки а, неперервні в точці а, g (x) відмінна від нуля в околі а і f(a) = g(a) = 0,

то границя відношення функцій при х а дорівнює границі відношення їх похідних,

якщо ця границя (скінчена або нескінченна) існує.

lim f (x)

x a g(x)

lim f (x) .

x a g (x)

Наприклад. Знайти границю lim	x2 1		ln x	.
x 1	e	x	e

Як видно, при спробі безпосереднього обчислення границі отримаємо

невизначеність виду 00 . Функції, які входять в чисельник і знаменник дробу задовольняють вимогам теореми Лопіталя:

f (x) = 2x +

1

;

g (x) = ex;

х

2x

1

f (x)

2 1

3

lim

x

.

g (x)

e x

e

e

x 1

Якщо при розв‟язуванні прикладу після застосування правила Лопіталя спроба обчислити границю знову приводить до невизначеності, то правило Лопіталя може бути застосовано другий раз, третій і т.д. доки не буде отримано результату. Це можливо лише в тому випадку, коли знов отримані функції в свою чергу задовольняють вимогам теореми Лопіталя.

x

Наприклад. Знайти границю lim

xe 2

.

x e

x

x

x

1

x) ;

g (x) 1 e x ;

f (x) e 2 (1

2

1

x

1

x

x

x

1

x

e

e

e

(4 x) ;

g (x) e x ;

f (x)

e 2

2

2

2

2

2

4

4