Математика для економістів Ден.. 2010 ч

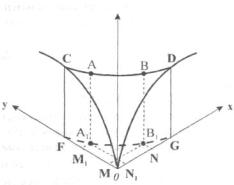
Крива байдужості представляє функцію, яка є окремим випадком кардиналістської функції корисності, що має тільки дві змінних. Математично - це лінія рівня функції корисності. Лінією рівня функції корисності називається сукупність значень аргументів, для яких функція постійна:

TU = U(X, Y); U(X, Y) = const.

Побудуємо криву байдужості за допомогою тривимірного графіка.

На осях х та у відкладемо кількості товарів X і Y, на осі z - сукупну корисність цих двох благ. Якби споживач мав лише одне благо X, то сукупна корисність від його споживання зростала б по кривій 0 D , якби споживач купував лише благо Y, то сукупна корисність зростала б по кривій ОС.

Припустимо, що для кількості блага X, рівній 0G , його корисність становитиме величину DG . Така сама величина корисності для блага Y дорівнює CF для кількості OF , отже, DG = CF . Оскільки величина корисності є однаковою,

споживачу байдуже - мати 0G блага X чи OF блага У.

Так само може бути представлена множина інших комбінацій благ X і Y з

рівною корисністю, яка відповідатиме сукупній корисності кількості OF блага Y

або 0G блага X. Ми одержимо ряд точок (А, В і т.д.) на кривій CD і площу корисності CFGD для комбінацій благ ON і ОМ , ON і ОМ, і т.д. Ці комбінації благ

X і Y будуть байдужими для споживача, оскільки мають однакову корисність.

Тепер для спрощення аналізу перенесемо проекцію CD на площину Оху.

Такою проекцією є пунктирна лінія FG з точками А1, В1 графіка , що відображає комбінації благ X і Y з однаковою корисністю. Це і є крива байдужості.

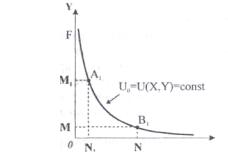
Рухаючись вздовж обраної кривої байдужості, споживач залишається на одному і тому ж рівні корисності, але може змінювати набір товарів у кошику.

Опуклість кривої байдужості до початку координат означає, що збільшення кількості одного товару в кошику супроводжується зменшенням кількості іншого на певну величину, тобто споживач може лише замінювати один товар іншим.

Кількість одного блага, від якої споживач змушений відмовитись, щоб одержати додаткову одиницю іншого блага, називається граничною нормою заміни.

Аналіз кривих байдужості дозволяє узагальнити їх властивості:

1) Криві байдужості не можуть перетинатися, оскільки кожна крива відповідає конкретному рівню корисності. Якби криві перетиналися, це означало б, що кошик точки перетину має не один, а декілька рівнів корисності, що суперечить припущенню щодо транзитивності уподобань споживача.

2) Криві байдужості, розташовані далі від початку координат,

відповідають наборам благ з вищим рівнем корисності, оскільки вища крива дозволяє споживачу одержувати більшу кількість обох благ порівняно з нижчою.

Споживач завжди прагне досягти найвищої з можливих кривих.

3) Криві байдужості мають від'ємний нахил, є спадними для абсолютної більшості благ. Від'ємний нахил кривої байдужості означає, що споживач повинен відмовитись від деякої кількості одного блага, щоб мати можливість одержати додаткові одиниці іншого блага і залишитись на тому ж рівні корисності.

Позитивний нахил кривої є неможливим, оскільки кошики будуть містити більшу або меншу кількість обох товарів й не належатимуть до одного набору байдужості.

4) В міру просування донизу по кривій байдужості вона стає пологішою,

випрямляється. Гранична норма заміни товару є спадною, оскільки готовність

споживача до заміни товару Y товаром X зменшується з нарощуванням споживання

X.

Приклади

1. Обчислити похідну функції z=x2 +y2x в точці А(1,2) за напрямом вектора

АВ . В(3, 0).

Розв'язок. Спочатку визначимо координати вектора АВ .

АВ =(3-1; 0-2) = (2; -2) = 2 i

2 j .

Визначимо модуль цього вектора:

AB

=

8

2 2 .

Знаходимо частинні похідні функції z в загальному виді:

z

2x

y 2

;

z

2 yx;

x

y

Значення цих величин в точці А :

z

6;

z

4;

x

y

Для знаходження напрямних косинусів вектора

АВ виконаємо наступні

перетворення:

S =

AB

2

2

i cos

j cos

i

j

AB

2

2

2

2

За величину S

приймаємо

довільний

вектор, направлений вздовж заданого

вектора, тобто визначаючого напрямок диференціювання.

Звідси отримаємо значення напрямних косинусів вектора АВ :

cos

=

2

;

cos

= -

2

2

2

Отримаємо:

z

2

2

- значення похідної заданої функції за напрямом

6

4

2

s

2

2

вектора АВ .

2. Знайти лінії рівня функції z

x2

y2

2x

2 y .

Розв'язок. Лінії рівня даної функції – це сім‟я кривих на площині Oxy , що описується рівнянням

x2 y2 2x 2 y C або (x 1)2 ( y 1)@ 2 C .
Остане рівняння описує сім‟ю кіл з центром в точці O1 (1,1) радіуса r	2 C .

Поверхня обертання (параболоїд), що описується заданою функцією, становиться

„крутіше” по мірі її віддалення від осі, яка визначається рівняннями x 1, y

1.

3. Знайти градієнт і його модуль функції z

xy

в точці M (0,1) .

x

y 1

Розв‟язок.

gradz

z

,

z

=

y( y

1)

,

x(x

1)

.

(x y 1)2

(x y 1)2

x y

При x

0 і y

1 отримаємо:

1,0 ,

gradz

1.

gradz

(0,1)

x2

y2

4. Знайти поверхні рівня функції u

2x

2 y

z .

Розв'язок. Відповідно означенню поверхні рівня, маємо x2

2x

y2

2 y

z

c , звідки

z (x 1)2

( y 1)2

C , де С=с+2. Отже, поверхнями рівня даної функції є

параболоїди

обертання

з

віссю

x

1, y

1,

паралельній осі

Oz ,

вершини яких

лежать в точках з координатами (1, 1,

C) .

Завдання

1.

Побудувати лінії рівня функцій:

1.

z xy ;

2. z x y ;

3. z

y x2 .

2.

Знайти градієнт і його модуль для функцій в зазначених точках:

1.

z

4

x2

y2 , в точці M (1,2) ; 2.

z

(x

y)2 ,

M (0,3) ; 3. u

xyz ,

M (3,

1,2) .

3.

Знайти частинні похідні другого порядку:

x2

xey , 3.

exy ) ; 4. z

x2 y .

1.

z

, 2. z

z

ln(x

1

2 y

Питання для самоконтролю

1.Дати означення диференційованості функції z 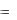f (x, y) .

2.Довести теорему про неперервність диференційованої функції.

3.Вивести достатні умови диференційованості функції двох змінних.

4.Що називається лінією рівня функції z 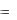f (x, y) ? Навести приклад.

5.Що називається поверхнями рівня функції u 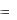f (x, y, z) ?

Література [1,2,4]

ПРАКТИЧНЕ ЗАНЯТТЯ № 16, 17

Тема 11. Екстремум та умовний екстремум функції багатьох змінних

Мета заняття. Вивчення теми надасть студентам можливість набути навички дослідження функції на екстремум, знаходити найбільше та найменше значення функції в замкненій області. Вивчити поняття умовного екстремуму функції багатьох змінних і метод Лагранжа, типові оптимізаційні задачі економіки в сфері виробництва і споживання: прибуток від виробництва товарів, задача цінової дискримінації, оптимізаційний розподіл ресурсів, гранична норма заміни факторів.

План заняття

1.Екстремум функції багатьох змінних.

2.Найбільше та найменше значення функції багатьох змінних в замкненій області.

3.Умовний екстремум. Метод Лагранжа.

4.Оптимізаційні задачі економіки.

Методичні рекомендації до практичного заняття

Екстремум функції багатьох змінних

Означення. Якщо для функції z 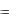f (x, y) , визначеній в деякій області, в

деякому околі точки М0(х0,у0) виконується нерівність

f (x0 , y0 ) f (x, y) ,

то точка М0 називається точкою максимуму.

Означення. Якщо для функції z 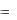f (x, y) , визначеній в деякій області, в

деякому околі точки М0(х0,у0) виконується нерівність

f (x0 , y0 ) 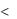f (x, y)

то точка М0 називається точкою мінімуму.

Теорема. (Необхідні умови екстремуму). Якщо функція f (x, y) в точці

(х0,у0) має екстремум, то в цій точці або обидві її частинні похідні першого порядку дорівнюють нулю f x (x0 , y0 ) 0, f y (x0 , y0 ) 0 , або хоча б одна з них не існує.

Цю точку (х0, у0) будемо називати критичною точкою.

Теорема. (Достатні умови екстремуму). Нехай в околі критичної точки (х0,

у0) функція f (x, y) має неперервні частинні похідні до другого порядку включно.

Розглянемо вираз:

D(x, y) 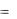f x2 (x, y) f y 2 (x, y) f xy (x, y) 2

1) якщо D(x0, y0) > 0, то в точці (х0, у0) функція f (x, y) має екстремум, якщо

f x2 (x0 , y0 ) 0 - максимум,

якщо f x2 (x0 , y0 ) 0 - мінімум;

2)якщо D(x0, y0) < 0, то в точці (х0, у0) функція f (x, y) не має екстремуму;

Увипадку, якщо D = 0, висновок про наявність екстремуму зробити не можна.

Умовний екстремум

Умовний екстремум знаходиться, коли змінні х і у, що входять в функцію

u f (x, y) , не є незалежними, тобто існує деяке співвідношення	(х,	у)=0,	яке
називається рівнянням зв’язку. Щоб знайти умовний екстремум функції		f (x, y)	при
наявності співвідношення (х, у)=0, записують функцію Лагранжа:

F(x, y) 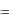f (x, y) 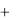(x, y) ,

де 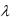- невизначений постійний множник, і шукають звичайний екстремум цієї допоміжної функції. Необхідні умови екстремуму зводяться до системи трьох рівнянь

F			f			0,
x			x		x
F			f			0,
y			y		y
(x, y)				0

з трьома невідомими x, y, , можна визначити ці невідомі.

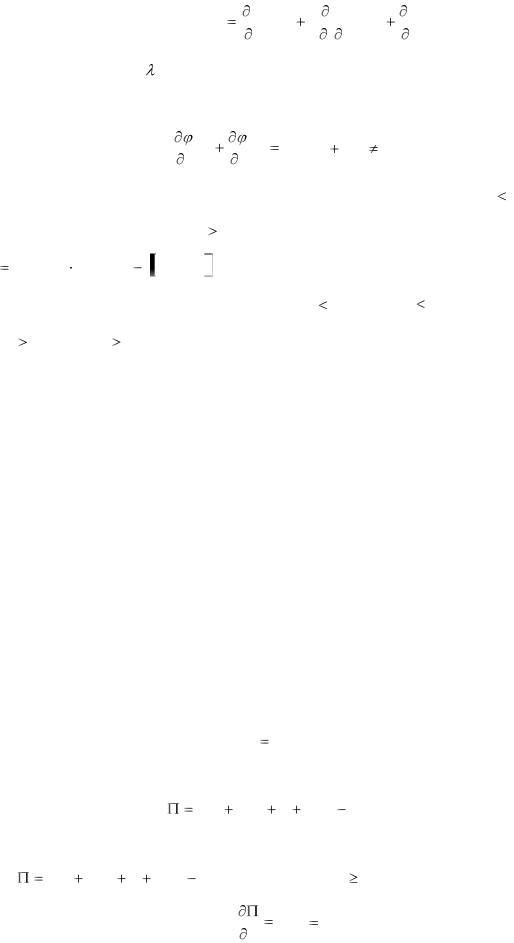
Питання про існування і характер умовного екстремуму вирішується на основі вивчення знаку другого диференціалу функції Лагранжа

d 2 F (x, y)	2 F	dx2	2	2 F	dxdy	2 F	dy2
	x2			x y		y2

для системи значень x, y, , отриманої із необхідної умови існування екстремуму, за умови, що dx і dy пов‟язані рівнянням

dx

dy 0 , dx2

dy2

0

x

y

А саме, функція

f (x, y) має умовний максимум, якщо d 2F

0 , і умовний

мінімум,

якщо

d 2F

0.

Зокрема,

якщо

детермінант

D(x, y) F ''

(x, y) F '' (x, y)

F ''

(x, y) 2

в стаціонарній точці додатній, то

в цій точці є

xx

yy

xy

умовний максимум функції f (x, y) ,

якщо F ''

0 (або

F ''

0 ), і умовний мінімум,

xx

yy

якщо F ''

0 (або F ''

0 ).

ee

yy

Найбільше та найменше значення функції Функція, яка диференційована в обмеженій замкненій області, досягає свого

найбільшого (найменшого) значення або в стаціонарній точці або в точці границі області. Розглянемо знаходження найбільшого (найменшого) значення функції в замкненій області на прикладі (див. приклад 1).

Застосування в задачах економіки Прибуток від виробництва різних видів продукції

Розглянемо типову задачу знаходження екстремуму функції багатьох

змінних, що виникає в економіці.

Нехай x1, x2 ,...., xm - кількість вироблених m видів

продукції,

а їх

ціни

відповідно

P , P ,...., P

(всі

P - постійні величини). Нехай

1 2

m

i

витрати на виробництво цих видів продукції задані функцією витрат

C S (x1, x2 ,..., xm ) .

Тоді функція прибутку має вигляд

P x

P x ...

P x

x

S (x , x ,..., x ) .

1 1

2

2

m

1 2

m

Максимум прибутку доцільно шукати як умову екстремуму функції багатьох

змінних

P x

P x

... P x

x

S (x , x ,..., x )

при

x

0 (при відсутності інших умов)

1 1

2 2

m

1 2

m

i

0 ,

i

1,2,..., m.

xi

Ця умова приводить до системи алгебраїчних рівнянь відносно змінних xi

	Pi	S	0	, i 1,2,..., m.
		xi

Остання система рівнянь реалізує відоме правило економіки: гранична вартість (ціна) продукції дорівнює граничним витратам на виготовлення цієї продукції. Розв‟язком цієї системи рівнянь є набори, які складаються із m значень кожен.

Максимізація прибутку виробництва однорідної продукції Функція прибутку обчислюється за формулою

(K, L)	PF(K, L) WL RK ,
де F(K, L) - виробнича функція,	P -	ціна продукції, W і R - відповідно,
факторні ціни на працю і капітальні витрати,		L і K - відповідно, витрати трудових

ресурсів і капіталу. Розглянемо дві задачі, пов‟язані з визначенням максимуму прибутку.

1. Точка (K0 , L0 ) - називається оптимальним планом, якщо в ній функція

прибутку приймає максимальне значення. Знайти граничну норму заміщення виробничої функції F при оптимальному плані.

В точці локального екстремуму перші						похідні функції прибутку (K, L)
дорівнюють нулю, звідки маємо систему двох рівнянь:
		PF ' (K		, L ) R 0 , PF '		(K	, L ) W 0 .
		K	0	0	L	0	0
Як відомо, гранична норма заміщення першого ресурсу другим обчислюється
за формулою	F '	F ' , звідки при оптимальному плані отримаємо:						W R .
	L	K
2. Максимізація функції прибутку. Знайти оптимальний план і максимум
функції прибутку, якщо F (K , L)			2(KL)1|3 . Таким чином, функція прибутку в даному
випадку має вигляд
				(K , L)	2(KL)1|3	WL RK .

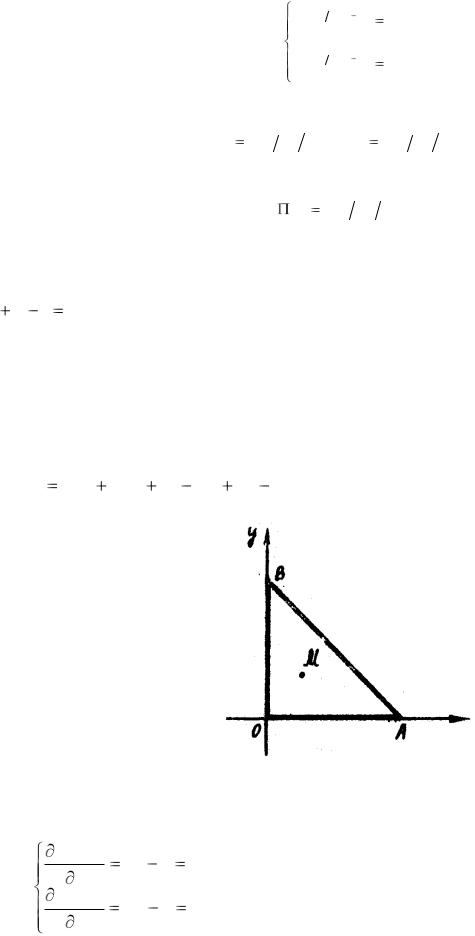
Умови екстремуму приводять до системи двох лінійних алгебраїчних рівнянь відносно координат K 0 і L0 оптимального плану:

		2			PL1	3 K	2|3	R,
							0
		3			0
		2			PL1	3 K	2|3	W .
							0
		3			0
Звідки отримаємо координати оптимального плану:
K	0	(2P 3)3			R2W ,		L (2P 3)3 RW 2 .
							0
Підстановка цих величин в функцію прибутку дає її максимум:
		ma[			(2P 3)3			RW .

Приклади

1. На площині заданий трикутник ОАВ , утворений осями Ох, Оу і прямою x y 1 0 . Потрібно знайти таку точку цього трикутника, для якої сума

квадратів її відстаней до вершин трикутника була б найменшою.

Розв‟язування. Так як вершини О, А і В трикутника мають відповідно

координати (0;0),(1;0),(0;1) , то можемо написати вираз для вищезгаданої суми квадратів відстаней від шуканої точки M (x, y) до вершин трикутника:

z 2x 2 2 y 2 (x 1)2 ( y 1)2 .

Знаходимо й прирівнюємо до нуля частинні похідні функції; одержуємо наступну систему рівнянь:

f (x, y)

x

f (x, y)

y

6x 2 0,

6 y 2 0.

	З цієї системи визначаємо x						1	, y	1	. Точці M (		1	;	1	) відповідає значення
							3		3		3		3
функції, що дорівнює					4	.
					3
	Досліджуємо далі функцію на контурі трикутника. При дослідженні функції
z	2x2	2 y2	(x	1)2		( y 1)2 у точках катета ОА					покладаємо y 0 . Одержуємо
z	2x2	(x	1)2	1 ,

причому x [ 0,1] . Знайдемо критичні точки цієї функції в інтервалі ( 0,1) , маємо

												dz	6x	2		0, x				1		.
												dx							3
					Значення функції у цій точці і на кінцях проміжку відповідно дорівнюють:
	z(	1	)			5	, z(0) 2 ,		z(1)		3 .
		3			3
					Таким чином, функція приймає найменше значення, що дорівнює																							5	в точці з
																									3
	координатою x								1	(відповідно y 0 ). Аналогічно досліджується функція на катеті
								3
	ОВ, найменше значення функції дорівнює													5		і досягається в точці з координатою
														3
	y			1	(відповідно x						0 ).
		3
					Для дослідження значень функції z											2x 2	2 y 2							(x 1) 2 ( y	1) 2 на гіпотенузі
	АВ підставимо у функцію замість змінної y															її вираз через x , знайдений з рівняння
	x		y			1 прямої АB: результаті одержуємо
											z 3x 2		3(x	1) 2 ,			x		[0;1] .
					Найменше значення функції на гіпотенузі АВ знаходиться																				так само, як і на
	катетах ОА й ОВ. Воно досягається в точці															M 2	(	1	;		1		)	і дорівнює		2	. Порівнюючи
																	2		2						3

отримані значення функції, одержуємо, що найменше значення, яке дорівнює 43 ,

функції приймає в точці M1(13 ; 13) .