Математика для економістів Ден.. 2010 ч

Завдання

1. Знайти екстремум функції двох змінних:

В. 1	Z x 2		xy	y 2	3x 6 y.	В. 2	Z 3x
В. 3	Z	x 2	xy	y 2	6x 3y.	В. 4	Z	3x
В. 5	Z	x 2	3xy y 2		6x 4 y.	В. 6	Z	2x

2	x3	3y 2	4 y.
2	4x	3y 2	x3 .
2	3xy	y 2	4x 6 y.

2. Знайти найбільше та найменше значення функції Z в області D.

В. 1 Z x 3y;		D : x 2	y 2	4.
В. 2 Z x 2y 5;		D : x 0; y 0; x y 2.
В. 3	Z 3x 4y 5;	D :x 0; y 0; x y 1.
В. 4	Z xy;	D : 1 x 1; 2 y 2.
В. 5	Z 4x y;	D : x 2	y 2	1.
В. 6	Z 4x 3y 2; D : x 0; y 0; y x 1.

Питання для самоконтролю

1.Що називається найбільшим і найменшим значенням функції з n невідомими?

2.Які достатні умови існування екстремуму функції двох змінних?

3.Записати схему дослідження функції двох змінних на екстремум.

4.У чому полягає метод множників Лагранжа ?

5.За яких умов функція двох змінних називається опуклою вниз?

6.Сформулювати умови існування точки умовного максимуму (мінімуму).

Література [1,2,4]

ПРАКТИЧНЕ ЗАНЯТТЯ № 18

Модульний контроль №1

Модуль І. Вища математика

Змістовий модуль ІV. Інтегрування функцій. Диференціальні та різницеві

рівняння

f (x)

ПРАКТИЧНЕ ЗАНЯТТЯ № 19, 20

Тема 12. Інтегральне числення

Мета заняття. Вивчення теми надасть студентам можливість знати основи інтегрального числення, зокрема поняття невизначеного інтегралу і основні методи інтегрування.

План заняття

1.Первісна функція.

2.Невизначений інтеграл та його властивості.

3.Основні методи інтегрування.

Методичні рекомендації до практичного заняття

Первісна функція

Означення. Функція F(x) називається первісною функцією функції f(x) на відрізку [a,b] , якщо в будь-якій точці цього відрізку виконується рівність:

F (x) = f(x).

Необхідно зазначити, що первісних для однієї і тієї ж функції може бути нескінченно багато. Вони будуть відрізнятись один від одного на деяке постійне число:

F1(x) = F2(x) + C.

Невизначений інтеграл

Означення. Невизначеним інтегралом функції називається сукупність первісних функцій, які визначені співвідношенням: F(x) C .

Записують: f (x)dx F (x) C .

Умовою існування невизначеного інтегралу на деякому відрізку є неперервність функції на цьому відрізку.

Властивості:

1. f (x)dx (F (x) C)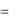f (x); 2. d f (x)dxf (x)dx;

3.	dF(x)	F (x) C;	4. C f (x)dx C f (x)dx;
5.	(u v	w)dx udx vdx	wdx; де u, v, w – деякі функції від х.

Знаходження значення невизначеного інтегралу пов‟язано головним чином зі знаходженням первісної функції.

Таблиця основних інтегралів

Інтеграл

Значення

Інтеграл

Значення

1

tgxdx

-ln

cosx

+C

9

e x dx

ex + C

2

ctgxdx

ln

sinx

+ C

10

cos xdx

sinx + C

3

a x dx

a x

11

sin xdx

-cosx + C

C

ln a

4

dx

1

arctg

x

C

12

1

dx

tgx + C

a2

x2

cos2

a

a

x

5

dx

1

ln

x

a

C

13

1

dx

-ctgx + C

x2

a 2

sin2

2a

x

a

x

6

dx

14

dx

x

ln

x

x 2

a 2

C

arcsin a

+ C

x 2 a 2

a 2

x 2

7

x

dx

x

1

C,

1

15

1

dx

ln

tg

x

C

cos x

1

2 4

8

dx

ln

x

C

16

1

dx

ln

tg

x

C

x

sin x

2

Методи інтегрування

Розглянемо три основних методи інтегрування.

Безпосереднє інтегрування

Метод безпосереднього інтегрування – інтегрування за допомогою таблиці основних інтегралів та властивостей невизначеного інтеграла. Цей метод застосовується лише для деяких обмежених класів функцій.

Метод заміни змінної (підстановки)

Теорема. Якщо потрібно знайти інтеграл f (x)dx , але важко відшукати, то за допомогою заміни x= (t) і dx= (t)dt отримаємо:

f (x)dx f ( (t)) (t)dt .

Функцію намагаються обирати таким чином, щоб права частина зазначеної формули набула зручного для інтегрування вигляду.

Наприклад. Знайти невизначений інтеграл sin x cos xdx.

Зробимо заміну змінної t = sinx, dt = cosxdt.

1/ 2

2

3 / 2

2

3 / 2

tdt

t

dt

t

C

sin

x C.

3

3

Інтегрування частинами Якщо u (x) і v (x) - диференційовані функції, то

udv uv vdu .

Ця формула дозволяє знаходити інтеграли багатьох елементарних функцій.

Інколи, щоб звести інтеграл до табличного, доводиться застосовувати формулу інтегрування частинами декілька разів.

Можливі такі випадки.

1.Якщо інтеграл має вигляд P(x) sin xdx , P(x) cos xdx або P(x)e x dx , де P(x) -

многочлен, то u = P(x) , а dv - вираз, що залишився;

2.	Якщо	інтеграл	має	вигляд	ln xP(x)dx ,	arctgxP(x)dx ,	arcctgxP(x)dx ,
	arcsin xP(x)dx ,		arccosxP(x)dx , де P(x) - многочлен, то dv = P(x) , а u - вираз,
	що залишився;
3.	Якщо	інтеграл	має	вигляд	eax sin bxdx,	eax cosbxdx ,	sin(ln x)dx або
	cos(lnx)dx , то після двократного інтегрування частинами приходимо до

початкового інтегралу з деяким коефіцієнтом. Розв‟язок здобутого лінійного рівняння і є первісною для шуканого інтеграла.

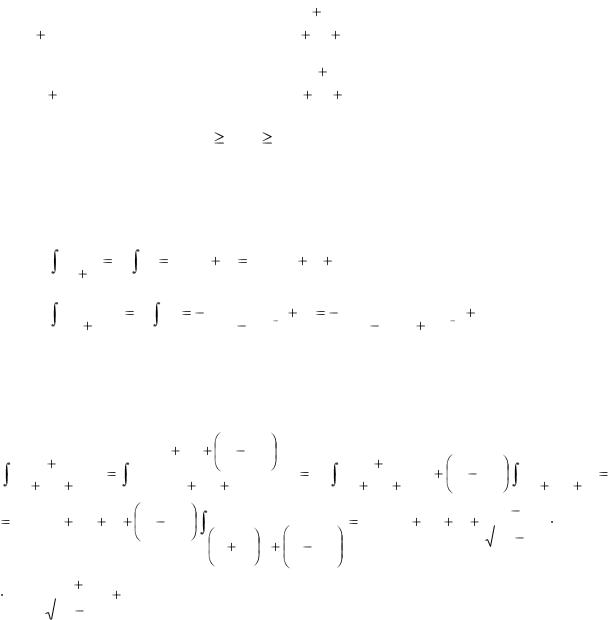
Інтегрування елементарних дробів

Означення. Елементарними називаються дроби наступних чотирьох типів:

1

Mx

N

I.

;

III.

;

ax

b

ax2

bx

c

II.

1

;

IV.

Mx

N

(ax

b)m

(ax2

bx

c)n

m, n – натуральні числа (m

2, n 2) і b2 – 4ac <0.

Перші два типи інтегралів від елементарних дробів досить просто приводяться до табличних підстановкою t = ax + b.

I.

dx

1

dt

1

1

ln

ax b

ln

t

C

C.

ax

b

a

t

a

a

II.

dx

1

dt

1

C

1

C;

(ax

b)m

a

t m

a(m

1)t m 1

a(m 1)(ax b)m 1

Розглянемо метод інтегрування елементарних дробів виду III.

Інтеграл дробу виду III може бути зображений у вигляді:

A

(2x

p)

B

Ap

Ax

B

dx

2

2

dx

A

2x p

dx B

Ap

dx

x 2

px q

x 2

px q

2 x 2

px q

2

x 2 px q

A

Ap

dx

A

ln

x 2

2B

Ap

ln

x 2

px q

B

px q

2

2

2

p 2

2

p

4q p 2

x

q

2

4

arctg

2x

p

C

4q

p 2

Отримали в загальному вигляді зведення інтегралу дробу виду III до двох табличних інтегралів.

Розглянемо застосування зазначеної вище формули на прикладі:

		7x 2									84x						24										84x		24			u	6x			5; du						6dx;
							dx														dx										dx			u		5
																																						;
3x 2					5x	4			36x 2						60x			48									(6x 5)2		23			x
																																	6
1			14u			70 24		du			7				udu			23									du		7	ln(u 2		23)	23					arctg		u				C Взагалі,
6					u 2	23					3				u 2		23 3 u 2 23 6																3 23							23
	7	ln			36x 2	60x		48						23		arctg				6x					5		C.
6													3
																		23

якщо у трьохчлена ax2 + bx + c вираз b2 – 4ac >0, то дріб за означенням не є елементарною, однак, її можна інтегрувати зазначеним вище способом.

Розглянемо тепер методи інтегрування дробів IV типу.

Спочатку розглянемо частинний випадок при М = 0, N = 1.

Тоді інтеграл виду

dx

можна шляхом виділення в знаменнику повного

(ax2

bx

c)n

квадрату зобразити у вигляді

du

. Зробимо наступне перетворення:

(u 2

s)n

du

1 s u 2

u 2

du

1

du

1

u 2 du

.

(u 2

s)n

s (u 2

s)n

s (u 2

s)n 1 s (u 2

s)n

Другий інтеграл, що входить в цю рівність, будемо інтегрувати частинами.

dv1

udu

;

u1 u;

du1

du;

(u 2

s)n

Позначимо:

udu

1

v1

;

(u 2

s)n

2(n

1)(u 2

s)n 1

u 2 du

u

1

du

;

(u 2

s)n

(2n

2)(u 2

s)n 1

2n

2

(u 2

s)n 1

Для початкового інтегралу отримали:

du

1

du

u

1

du

(u 2

s)n

s (u 2

s)n 1

s(2n

2)(u 2

s)n 1

s(2n

2)

(u 2

s)n 1

du

u

2n

3

du

.

(u 2

s)n

s(2n

2)(u 2

s)n 1

s(2n

2)

(u 2

s)n 1

Отримана формула називається рекурентною. Якщо застосувати її n-1 разів,

то отримаємо табличний інтеграл

du

.

u 2

s

Повернемося тепер до інтегралу від елементарного дробу виду IV в

загальному випадку.

Mx

N

Mx

N

u

2ax

b; du 2adx;

dx (4a)n

dx

u b

(ax2

bx c)n

(2ax b)2

(4ac b2 ) n

x

; s 4ac b2 ;

2a

В

M (u b)

N

(4a)n

(4a)n M

udu

2aN

Mb

du

2a

du

2a

(u 2

s)n

2a 2a (u 2 s)n

2a

(u 2

s)n

отриманій рівності перший інтеграл за допомогою підстановки t=u2+s зводиться до

	табличного	dt	, а до другого інтегралу застосовується розглянута вище рекурентна
		t n

формула (див. приклади).

Інтегрування раціональних функцій

Інтегрування раціональних дробів

Для того, щоб проінтегрувати раціональний дріб необхідно розкласти її на елементарні дроби.

	Теорема. Якщо R(x)	Q(x)	- правильний раціональний дріб, знаменник P(x)
		P(x)

якої є добутком лінійних і квадратичних множників (відмітимо, що будь-який многочлен з дійсними коефіцієнтами може бути записано в такому виді: P(x)=(x- a) …(x-b) (x2+px+q) …(x2+rx+s) ), то цей дріб може бути розкладений на елементарні за наступною схемою:

Q(x)

A1

A2

...

A

...

B1

B2

...

B

M1 x N1

P(x)

x a (x a)2

(x a)

(x b)

(x b)2

(x b)

x2

px q

де Ai, Bi,

M 2 x N2

M x N

R1 x S1

R2 x S2

R x S

...

...

...

(x2

px q)2

(x2

px q)

x2 rx s (x2

rx s)2

(x2

rx s)

Mi, Ni, Ri, Si – деякі постійні величини.

При інтегруванні раціональних дробів застосовують розклад початкового дробу на елементарні. Для знаходження величин Ai, Bi, Mi, Ni, Ri, Si застосовують так званий метод невизначених коефіцієнтів, суть якого полягає в тому, що для того, щоб два многочлена були тотожньо рівні, необхідно і достатньо, щоб були рівні коефіцієнти при однакових степенях х.

Застосування цього методу розглянемо на конкретному прикладі:

Обчислити інтеграл:

9x3

30x2

28x

88

dx

(x2

6x

8)(x2

4)

Так як ( x 2

6x 8)(x 2

4)

(x

2)(x 4)(x 2 4) , то

9x3

30x2

28x 88

A

B

Cx D

(x

2)(x 4)(x2 4)

x 2

x

4

x2

4

Приводячи до спільного знаменника і прирівнюючи відповідні чисельники,

отримаємо:

A(x

4)(x 2

4)

B(x 2)(x 2

4) (Cx

D)(x 2

6x

8)

9x3

30x 2 28x 88

( A B C)x3

( 4A 2B 6C D)x2

(4A 4B 8C 6D)x ( 16A 8B 8D)

9x3

30x2

28x 88.

A

B

C

9

C

9

A

B

4A 2B 6C D 30

D 30 4A 2B 54 6A 6B

4A 4B 8C 6D 28

2A 2B 4C 3D 14

16A 8B 8D 88

2A B D 11

C

9

A

B

C

9 A

B

D 24 2A 4B

D 24 2A 4B

2A 2B 36 4A 4B 72 6A 12B 14

4A 10B 50

2A B 24 2A 4B 11

4A 5B 35

C

9

A

B

C

9

A

B

A

5

D 24 2 A 4B

D 24 2A 4B

B 3

4 A 10B 50

4A

10B

50

C

1

50

10B 5B

35

B

3

D

2

Отже:

5

3

x

2

x

2

dx

dx

dx

5 ln

x 2

3ln

x 4

dx

dx

x 2

x 4

x 2

4

x 2

4

x 2

4

1

ln(x 2

4) arctg

x

5 ln

x

2

3ln

x

4

C.

2

2

Інтегрування деяких тригонометричних функцій

Інтеграл виду R(sin x, cos x)dx .

Тут R – деяка раціональна функція від змінних sin x і cos x .

Інтеграли цього виду обчислюються за допомогою підстановки t tg 2x . Ця підстановка дозволяє перетворити тригонометричну функцію в раціональну.

2tg

x

1 tg

2

x

2

2t

,

2

1 t 2

sin x

cos x

;

1

tg

2 x

1

t 2

1

tg

2

x

1

t 2

2

2

Тоді

x

2arctgt;

dx

2dt

;

1 t 2

Таким чином:

R(sin x, cos x)dx

R

2t

,

1

t 2

2

dt

r(t)dt.

1

t 2

1

t 2

1 t 2

Зазначене перетворення називається універсальною тригонометричною

підстановкою.

Наприклад. Обчислити інтеграл:

2dt

dx

dt

dt

1

t 2

2

2

4 sin x

3cos x

5

2t

1

t 2

8t

3

3t 2

5

5t 2

2t 2

8t 8

4

3

5

За

1

t 2

1

t 2

dt

dt

1

C

1

C.

t 2

4t 4

(t 2)2

t

2

tg

x

2

2

допомогою цієї підстановки завжди можна перевести тригонометричну функцію в раціональну і обчислити відповідний інтеграл. До недоліків можна віднести те, що при перетворенні може утворитись достатньо складна раціональна функція.

Інтегрування деяких ірраціональних функцій

Далеко не кожна ірраціональна функція може мати інтеграл, виражений елементарними функціями. Для знаходження інтеграла від ірраціональної функції слід застосовувати підстановку, яка дозволить перетворити функцію в раціональну,

інтеграл від якої може бути знайдено, як відомо, завжди.

Розглянемо деякі підстановки для інтегрування різних типів ірраціональних функцій.

Інтеграл виду

R

x, n

ax

b

dx

де n- натуральне число.

cx

d

За допомогою підстановки

n

ax

b

t функція раціоналізується.

cx

d

ax b

t n ;

x

t n

b

;

dx

t n

b

dt;

cx

d

a

ct n

a

ct n

t n

t n

Тоді

R

x, n

ax

b

dx

R

b

, t

b

dt

r(t)dt.

cx

d

a

ct n

a

ct n

Наприклад. Обчислити інтеграл:

dx

2dx

dx

2t 3 dt

t 2 dt

4 1

2x

t;

dt

;

2

3

2t 3

t 2

t 1

1 2x

4 1 2x

4 4

t

1 2x

2

t

t

dt

2 tdt

2

t

dt

t 2

2 1

1

dt

t 2

2t

2 ln

t 1

C

t

1

t

1

t

1

1 2x 241 2x 2 ln 41 2x 1 C.

Якщо до складу ірраціональної функції входять корені різних степенів, то в якості нової змінної доцільно взяти корені степеня, що дорівнює найменшому спільному кратному степенів корнів, що входять у вираз. Проілюструємо це на прикладі.

Наприклад. Обчислити інтеграл: