Математика для економістів Ден.. 2010 ч

y

2x2

y

x

.

3.

.

3.

x 1

x

2

В. 5

В. 6

1. y

1

;

1. y

1

;

25 x2

6x

25 x2

x

2. y

1

;

2. y

1

;

x 3 x 1 x 2

x x 2 x 1

3. y

x

3. y

x2

.

.

2x 1

2x 1

Інтегрування ірраціональних виразів

4. Знайти інтеграли для даних функцій:

В. 1

В. 2

В. 3

1.

y

x

;

1.

y

x

;

1.

y

x

;

x 2

x 2 2x 5

2x x 2

2x 5

5

6

3

2.

y

x

.

2.

y

x

.

2.

y

x

.

x

1

1

x

1

3 x

В. 4

В. 5

В. 6

1.

y

x

;

1.

y

x

;

1.

y

x

;

5 x 2

2x x 2

x 2 2x 3

2x

5

1

1

2.

y

.

2. y

.

2. y

1

x

.

1 2x

4 1 2x

x 2 x2

2x

x 2 x

Інтегрування тригонометричних функцій

5. Знайти інтеграли для даних функцій:

В. 1

В. 2

В. 3

1.

y

1

;

1.

y

1

;

1.

y

1

;

sin x

cos x

5

3cos x

5

4sin x

2.

y

cos5 x

sin 2x;

2.

y

sin2 x cos2 x;

2.

y

1

2cos x 2 ;

3.

y

sin3x cosx;

3.

y

cos3x sin x;

3.

y

sin2x cos2x;

4.

y

4 x 2

.

4. y

1

.

4. y

x 2

.

x

x

4

x 2

x 2

4

В. 4

В. 5

В. 6

1.

y

1

;

1.

y

1

;

1. y

1

;

cos x

2sin x

2 cos x sin x

2 cos x 3sin x

2.

y

sin 2x

;

2.

y

tg 3 x;

2.

y

1

;

cos4 x

sin4

x

3.

y

tg 2 x;

3.

y

sin3 x

cos2 x;

3.

y

sin x cos2x;

4.

y

9 x

2

.

4.

y

x

1

.

4.

y

x

.

x

x 9

x 2

x 2

9

Питання для самоконтролю

31.Що називається первісною даної функції? Навести приклади.

32.Сформулювати теорему про існування первісної.

33.Сформулювати та довести основні властивості невизначеного інтеграла.

34.У чому суть інваріантності формули інтегрування?

35.Які раціональні дроби називаються елементарними?

36.Як інтегруються елементарні дроби?

37.Як інтегруються елементарні дроби?

38.Який раціональний дріб називається правильним?

39.Записати розкладання правильного раціонального дробу на елементарні дроби.

40.В чому полягає метод інтегрування раціонального дробу?

41.Записати розкладання багаточлена на лінійні множники та квадратні тричлени з дійсними коефіцієнтами.

42.Навести приклади інтегрування раціональних функцій.

43.Як обчислюються інтеграли 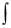sinn x cosm xdx ?

44.У якому випадку кажуть, що невизначений інтеграл не є елементарною функцією? Навести приклади.

Література [1,2,4]

ПРАКТИЧНЕ ЗАНЯТТЯ № 21, 22 Тема 12. Інтегральне числення

Мета заняття. Вивчення теми надасть студентам можливість знати поняття

та методи обчислення визначеного інтегралу, формулу Ньютона – Лейбниця.

[a,b]

План заняття

1.Визначений інтеграл та його властивості.

2.Формула Ньютона – Лейбниця.

3.Заміна змінної у визначеному інтегралі.

4.Формула інтегрування частинами для визначеного інтегралу.

5.Наближене обчислення визначеного інтегралу.

Методичні рекомендації до практичного заняття

Визначений інтеграл

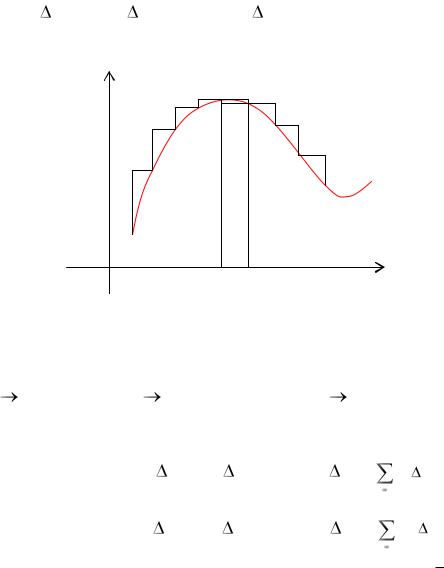
Нехай на відрізку [a, b] задана неперервна функція f(x). Позначимо через m і M найменше і найбільше значення функції на відрізку [a,b] . Розіб‟ємо відрізок

на частини (не обов‟язково однакові) n точками x0 < x1 < x2 < … < xn.

Тоді x1 x0= x1, x2–x1= x2, … ,xn–xn-1= xn;

y M

m

0 a

xi

b

x

На кожному із отриманих відрізків знайдемо найменше і найбільше значення

функції.

[x0,x1] m1, M1; [x1, x2]

m2, M2; … [xn-1, xn]

mn, Mn.

Складемо суми:

n

S n = m1 x1 + m2 x2 + … +mn xn = mi

xi

i 1

n

S n = M1 x1 + M2 x2 + … + Mn xn = M i

xi

i 1

Сума S називається нижньою інтегральною сумою, а сума S – верхньою інтегральною сумою.

Так як mi

Mi, то S n

S n,

а

m(b – a)

S n

S n

M(b – a).

Всередині кожного відрізку оберемо деяку точку .

x0 < 1 < x1, x1 < < x2, … , xn-1 < < xn.

Знайдемо значення функції в цих точках і складемо вираз, який називається

інтегральною сумою для функції f(x) на відрізку [a,b].

n

Sn = f( 1) x1 + f( 2) x2 + … + f( n) xn =

f ( i ) xi

i 1

Тоді можна записати: mi

xi

f( i)

xi

Mi

xi

n

n

n

Отже,

mi xi

f (

i ) xi

M i

xi

i 1

i 1

i

1

Sn

Sn

Sn .

Позначимо max xi – найбільший відрізок розбиття, а min

xi – найменший.

Якщо max xi

0,

то

число

відрізків

розбиття

відрізка

[a,b]

прямує

до

нескінченності.

n

n

Якщо Sn

f (

i ) xi

, то

lim

f (

i )

xi

S.

i 1

max

xi 0

i 1

Означення. Якщо при довільних розбиття відрізку [a,b] таких,

що max

xi

n

0 і довільному виборі точок i інтегральна сума Sn

f ( i ) xi

прямує до границі S,

i 1

яка називається визначеним інтегралом від f(x) на відрізку [a,b] .

b

Позначення :

f (x)dx , де а – нижня границя, b – верхня границя, х – змінна

a

інтегрування, [a,b] – відрізок інтегрування.

n

b

Означення. Якщо для функції f(x) існує границя

lim

f (

i ) xi

f (x)dx, то

max xi 0

i

1

a

функція називається інтегруємо на відрізку [a,b] .

n

b

Також виконуються твердження:

lim

mi

xi

f (x)dx

max xi

0

i 1

a

n

b

lim

M i

xi

f (x)dx

max xi

0

i

1

a

Теорема. Якщо функція f(x) неперервна на відрізку [a,b] , то вона інтегровна

на цьому відрізку.

Властивості визначеного інтеграла

	b	b
1)	Af (x)dx A f (x)dx;
	a	a
	b		b	b
2)	( f1 (x)	f2 (x))dx	f1 (x)dx	f2 (x)dx ;
	a		a	a
	a
3)	f (x)dx	0 ;
	a
				b	b
4)Якщо f(x) (x) на відрізку [a,b] a < b, то f (x)dx					(x)dx ;
				a	a

5)Якщо m і M – відповідно найменше і найбільше значення функції f(x) на відрізку [a,b], то:

b

m(b a) f (x)dx M (b a)

a

6)Теорема про середнє. Якщо функція f(x) неперервна на відрізку [a,b] , то на цьому відрізку існує точка така, що

b

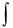f (x)dx (b a) f ( ) .

a

7)Для довільних чисел a, b, c справедлива рівність:

	b	c	b
	f (x)dx	f (x)dx	f (x)dx .
	a	a	c
b	a
8) f (x)dx	f (x)dx .
a	b

Узагальнена теорема про середнє. Якщо функції f(x) і (x) неперервні на

відрізку [a,b], і функція (х) знакопостійна на ньому, то на цьому відрізку існує точка , така, що

b	b
f (x) (x)dx f ( )	(x)dx .
a	a

Обчислення визначеного інтеграла

b

Нехай в інтегралі 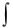f (x)dx нижня границя а=const, а верхня границя b

a

змінюється. Очевидно, що якщо змінюється верхня границя, то змінюється і значення інтегралу.

x

Позначимо f (t)dt = Ф(х). Знайдемо похідну функції Ф(х) по змінній верхній

a

границі х:

d	x
	f (t)dt f (x) .

dx a

Аналогічну теорему можна довести для випадку змінної нижньої границі.

Теорема. Для всякої функції f(x), неперервної на відрізку [a,b] , існує на цьому відрізку первісна, а отже, існує невизначений інтеграл.

Теорема (Теорема Ньютона – Лейбниця). Якщо функція F(x) – будь-яка первісна від неперервної функції f(x), то

b

f (x)dx F(x)		b	F(b) F(a) - формула Ньютона – Лейбниця.
		a

a

Обчислення визначених інтегралів практично нічим не відрізняється від всіх тих методів, які були розглянуті вище при знаходженні невизначених інтегралів.

Так само застосовуються методи підстановки (заміни змінної), метод інтегрування частинами, ті ж самі прийоми знаходження первісних для тригонометричних, ірраціональних і трансцендентних функцій. Особливістю є лише те, що при застосуванні цих прийомів потрібно розповсюджувати перетворення не лише на підінтегральну функцію, але і на границі інтегрування.

Замінюючи змінну інтегрування, не забути змінити відповідно границі інтегрування.

Заміна змінних

b

Нехай задано інтеграл 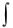f (x)dx , де f(x) – неперервна функція на відрізку [a,b] .

a

Введемо нову у відповідності з формулою x = (t).

Тоді якщо

1) ( ) = а, ( ) = b

[a,b]

2) (t) і		(t) неперервні на відрізку [						, ]
3) f(	(t)) визначена на відрізку [					,	], то
					b
					f (x)dx			f [ (t)] (t)dt
					a
Тоді									F(a) .
	f [	(t)] (t)dt	F[ (t)]		F[	(	)]	F[ ( )] F(b)
					Інтегрування частинами
Якщо функції u =			(x) і		v =		(x)	неперервні	на відрізку [a,b] , а також

неперервні на цьому відрізку їх похідні, то справедлива формула інтегрування частинами:

b	b	b
udv uv		vdu.
a	a	a

Наближене обчислення визначеного інтегралу Існує велика кількість функцій, інтеграл від яких не може бути виражено

через елементарні функції. Для знаходження інтегралів від таких функцій застосовують різноманітні наближені методи, суть яких полягає в тому, що підінтегральна функція замінюється “близькою” до неї функцією, інтеграл від якої виражається через елементарні функції.

Формула парабол

(формула Сімпсона або квадратурна формула)

(Томас Сімпсон (1710-1761)- англійський математик)

Розділимо відрізок інтегрування на парне число відрізків (2m). Площа криволінійної трапеції, обмеженої графіком функції f(x) замінимо на площу криволінійної трапеції, обмеженої параболою другого степеня з віссю симетрії,

паралельній осі Оу і яка проходить через точки кривої, зі значеннями f(x0), f(x1), f(x2).

Для кожної пари відрізків побудуємо таку параболу. Рівняння цих парабол мають вид Ax2 +Bx + C, де коефіцієнти А, В, С можуть бути легко знайдені за трьома точками перетину параболи з початковою кривою.

у

0 х0 х1 х2 х3 х4 х

y

0

Ax

2

Bx

0

C

0

y

Ax

2

Bx

C

1

1

1

y

2

Ax

2

Bx

2

C

2

Позначимо 2h

x2

x0 .

x2

x

3

x

2

x

( Ax 2 Bx C)dx A

2

S

B

Cx

3

2

x

0

x0

Якщо взяти х0 = -h, x1 = 0, x2 = h, то S

h

(2Ah 2

6C) .

3

Тоді рівняння значень функції мають вигляд:

y

0

Ah 2

Bh

C

y1

C

y

2

Ah 2

Bh

C

З урахуванням цього:

y

0

4y

y

2

2Ah2

6C .

1

Звідки маємо:

S

h

( y

4 y

y

)

0

2

3

1

Тоді

x2

h

f (x)dx

( y

4 y

y

)

3

0

1

2

x0

x2

h

f (x)dx

( y

4 y3

y4 )

3

2

x2

.......... .......... .......... .......... .......

Додаючи ці вирази, отримаємо формулу Сімпсона:

b

b a

f (x)dx

y

y

2( y

y

...

y

)

4( y

y

... y

) .

0

2m

2

4

2m 2

3

2m 1

6m

1

a

Чим

більше

взяти

число

m,

тем

більш точне

значення

інтегралу буде

отримано.

Приклади

1. Обчислити визначений інтеграл

1

x

sin t;

/ 2

/ 2

1

/ 2

1

x2 dx

0;

/ 2

1

sin2 t costdt

cos2 tdt

(1

cos2t)dt

2

0

0

0

0

1

1

/ 2

1

t

sin 2t

sin

.

2

2

4

4

4

0

2. Обчислити визначений інтеграл:

I

ln5 e x

e x

1

dx.

0

e x

3

e x

Нехай

1 =

t,

звідки

e0

1

0,

eln 5

1

2 . Отже, якщо х

змінюється

від 0

до ln5,

то

нова

змінна

t

змінюється

від 0

до 2. Функція

x ln t 2

1 , обернена до функції t

e x

1 ,

на відрізку [0;

2]

є монотонною і

неперервною разом з похідною

x

2t

на цьому відрізку. Маємо:

t

2

1

2	t 2	1 t 2tdt	2	t 2 dt	2		4		t
			2		2	1		dt 2 t 2arctg
0	t 2	4 t 2 1	0 t 2 4		0		t 2 4		2

2

0

4 .

	8
3. Обчислити наближене значення визначеного інтеграла		x3 16dx за
	2

формулою Сімпсона, розбивши відрізок інтегрування на 10 частин.

За формулою Сімпсона отримаємо:

	8				8		2
		x3	16dx					[ y(	2)	y(8) 2[ y(0) y(2) y(4) y(6)]
	2					6	5
	4[ y(		1) y(1)				y(3)		y(5)	y(7)]].

	m			0		1				2		3	4	5	6	7	8	9	10
	x			-2		-1				0		1	2	3	4	5	6	7	8
	f(x)			2.828		3.873				4		4.123	4.899	6.557	8.944	11.874	15.232	18.95	22.98
	8						8	2
		x3		16dx					[2.828			22.978 2[4		4.899	8.944	15.232]	4[3.873	4.123	6.557
	2					6		5
	11.874				18.947]]				91.151

Точне значення цього інтеграла – 91.173.

																																	Завдання
							1. Обчислити інтеграли:
	1						xdx							1																	1 e x xdx;								16							dx
1.										;			2.				1						xdx;							3.								4.													;
			1						x4
	0													0																	0								0				x 9						x
																																									1
																2 2 arcsin x
																															2
5.	13								dx			;	6.														dx;			7.			x cos xdx;					8.	2 e x dx							;
						4																																							2
								3		x				12								1 x			2						0								1			x
	2
													e																										e		1
	9				x			1															dx										3		xdx
9.										dx;			10.																;	11.							;	12.					ln x					1 dx;
																																			sin 2
	4						x	1					1 x				1						ln 2				x									x					0
																																	4

Питання для самоконтролю

1.Що називається визначеним інтегралом?

2.Записати формулу Ньютона-Лейбніця.

3.У чому полягає геометричний зміст визначеного інтегралу?

4.Сформулювати теорему про існування визначеного інтеграла.

5.Сформулювати та довести властивості збереження знака визначеного інтеграла.

6.Сформулювати та геометрично проілюструвати теорему про оцінку інтеграла.

7.Сформулювати та геометрично проілюструвати теорему про середнє значення.

8.Сформулювати теорему про похідну від інтеграла зі змінною верхньою

межею.

9.У чому полягає метод інтегрування частинами у визначеному інтегралі.

10.У чому полягає метод заміни змінної у визначеному інтегралі?

Література [1,2,4]

ПРАКТИЧНЕ ЗАНЯТТЯ № 23, 24 Тема 12. Інтегральне числення