Математика для економістів Ден.. 2010 ч

2n

1

arctg n n; 3.

1

1

n

1.

; 2.

; 4.

1

.

n 11 3 5

(2n 1)

n 1

n 2 n ln2 n

n 1

n

B. 6

1.

2

n

; 2.

2 4 2n

; 3.

n

1

; 4.

1

.

n 1 arcsin

n 1 ln e

n 1 5

n3

n 1 n

1

2n

n

Питання для самоконтролю

17.Що називається числовим рядом? Що називається загальним членом ряду?

Навести приклади.

18.Який ряд називається збіжним? Що називається його сумою? Який ряд називається розбіжним? Навести приклади.

19.Сформулювати та довести необхідну ознаку збіжності ряду. У чому полягає найпростіша достатня ознака розбіжності. Навести приклади.

Література [1,2,4]

ПРАКТИЧНЕ ЗАНЯТТЯ № 32, 33 Тема 14. Ряди та їх застосування

Мета заняття. Вивчення теми надасть студентам можливість знати знакозмінні ряди, умови абсолютної та умовної збіжності рядів. Також вивчити поняття степеневих рядів, визначати радіус та інтервал збіжності степеневого ряду.

А також застосування степеневих рядів до наближених обчислень.

План заняття

1.Знакозмінні ряди. Ознака Лейбниця.

2.Абсолютна і умовна збіжність рядів.

3.Ознаки Даламбера і Коші для знакозмінних рядів.

4.Функціональні ряди. Степеневі ряди.

5.Розвинення функції в степеневий ряд.

Методичні рекомендації до практичного заняття

Знакозмінні ряди

Нехай маємо ряд un , в якого є як додатні, так і від‟ємні члени. Такі ряди

n 1

називаються знакозмінними.

Серед знакозмінних рядів відокремлюють знакопочережні ряди, тобто ряди,

в яких додатні та від‟ємні члени чергуються.

Знакопочережний ряд можна записати у вигляді:

u

u

2

u

3

u

4

... ( 1)n 1 u

n

... , де u

n

0,

n

1,2,3,... .

1

Ознака Лейбниця

Якщо у знакопочережного

ряду u u

2

u

3

u

4

...

(

1)n 1 u

n

...

абсолютні

1

величини ui спадають u1

u2

u3

... і загальний член прямує до нуля un

0 ,

то ряд

є збіжним.

Абсолютна і умовна збіжність рядів

Розглянемо деякий знакозмінний ряд

u1

u2

...

un

...

un

(1)

і

ряд,

n 1

складений із абсолютних величин членів цього ряду

u1

u2

...

un

...

un

(2).

n 1

Теорема. Із збіжності ряду (2) випливає збіжність ряду (1).

Означення. Ряд

un

називається абсолютно збіжним,

якщо збігається ряд

un

.

Означення. Ряд un називається умовно збіжним, якщо він збігається, а ряд un розбігається.

Ознаки Даламбера і Коші для знакозмінних рядів

Ознака Даламбера. Нехай un - знакозмінний ряд. Якщо існує границя

	lim		un 1		, то при	<1 ряд un буде абсолютно збіжним, а при >1 ряд буде
			un
	n
	розбіжним. При =1 ознака не дає відповіді щодо збіжності ряду.
			Ознака Коші.			Якщо існує границя lim n			un		, то при <1 ряд un буде
						n

абсолютно збіжним, а при >1 ряд буде розбіжним. При =1 ознака не дає відповіді щодо збіжності ряду.

Функціональні ряди

Означення. Якщо членами ряду будуть не числа, а функції від х, то ряд

називається функціональним.

Дослідження на збіжність функціональних рядів складніше ніж дослідження числових рядів. Один і той самий функціональний ряд може при однакових значеннях змінної x збігається, а при інших – розбігається. Тому питання збіжності функціональних рядів зводиться до визначення тих значень змінної x , за яких ряд

збігається.

Сукупність таких значень називається областю збіжності.

Степеневі ряди

Означення. Степеневим рядом називається ряд вигляду

a	0	a x	a	2	x2	... a	n	xn ...	a	n	xn .
		1
									n 0

Теорема Абеля

(Нільс Хенрік Абель (1802 – 1829) – норвезький математик)

Теорема. Якщо степеневий ряд

a	0	a x	a	2	x2	... a	n	xn ...	a	n	xn
		1
									n 0

збігається при x = x1 , то він збігається і д отого абсолютно для всіх xx1 .

Наслідок. Якщо при х = х1 ряд розбігається, то він розбігається для всіх

	x		x1		.
			Таким чином, для кожного степеневого ряду існує таке додатне число R, що
при			всіх х таких, що			x	R ряд абсолютно збігається, а при всіх	x	R ряд

розбігається. При цьому число R називається радіусом збіжності. Інтервал (-R, R)

називається інтервалом збіжності.

Радіус збіжності може бути знайдено за формулами:

R lim	an 1		або R	lim		1			.
	an
					n
n				n
							n

Розвинення функцій в степеневі ряди Розвинення функцій в степеневий ряд має велике значення для розв‟язку

різних задач дослідження функцій, диференціювання, інтегрування і т.д. Задача

відшукання за заданою функцією

f степеневого ряду, для якого f

є його сумою,

називається задачею розвинення функції в степеневий ряд.

Припустимо, що функція f

у точці x0

має похідні всіх порядків. Тоді можна

побудувати степеневий ряд

a

n

(x

x

)n ,

0

n 1

де a

f (n) (x0 )

.

n

n!

Такий ряд називається рядом Тейлора функції f . Уразі, коли x0

0 , ряд

a

n

xn ,

n 1

де a

f (n) (0)

називають рядом Маклорена.

n

n!

У разі розвинення функції в степеневий ряд коефіцієнти ряду Тейлора відшукують, використовуючи п‟ять основних розвинень:

1)

e x

x n

;

n

1 n!

2)

cos x

(

1)n

x 2n

;

n 1

(2n)!

3)

sin x

(

1)n

1

x 2n 1

;

n 1

(2n

1)!

4)

ln(1

x)

(

1)n 1

x n

;

n

n

1

5)

(1

x)

1

C n xn , C n

(

1)...(

(n 1))

.

n!

n 1

Приклади

1. Знайти радіус збіжності степеневого ряду та дослідити його поведінку на границі інтервалу збіжності:

1 3x 32 x 2 33 x3 ... 3n 1 x n 1 ...

Розв’язок.

	Lim				an 1			Lim	3n			3;
					an				3	n	1
	n							n
R	1				1	.
				3
Ряд збіжний абсолютно для усіх значень x													1	,x	1	.
													3		3

Дослідити поведінку ряду на границі інтервалу збіжності x 13 .

Підставимо в поданий ряд x 13 , маємо: 1-1+1-1+… цей ряд розбіжний, тому

що не виконується необхідна умова збіжності ряду lim un 0.

n

Тепер підставимо в поданий ряд x 13 , маємо: 1+1+1+1+… оскільки не виконується необхідна умова збіжності, цей ряд також розбіжний.

Завдання

Визначити, які знакозмінні ряди збігаються абсолютно, умовно або розбігаються:

(

1)n

(

1)n

В. 1

;

2.

.

1 (n

1)!

n

1 2n

1

n

(

1)n n

;

(

1)n

В. 2

2.

n 2

.

n 1 2n3

1

n ln n

B. 3

(

1)n tg

;

2.

(

1)n

.

n

2

n

1 (n

1)3

n 1

(

1)n n2

( 1)n 3n

B. 4

;

2.

n 1

.

n 1

3n

4n 1

(

1)n

;

(

1)n

B. 5

2.

n 2

.

n ln4 n

n 1

4n 1

(

1)n

;

sin n

B. 6

2. n

1

.

n 1 ln(n

1)

n2

Степеневі ряди

1. Знайти область збіжності степеневих рядів

В 1.

10x 100x2

...

10n xn ....

В 2.

x

x2

x3

...

xn

....

20

30

n 10n

1

В 3.

1

x

2!x2

...

n!xn ... .

В 4. 1

2x2

4x4 ...

2n 1 x2(n 1) ....

В 5.

1

1

x

2

x

2

...

n

x

n

... .

В 6.

x

1

x

3 1

x

5

...

( 1)n 1

x

2n 1

...

1!

2!

n!

3 3!

5 5!

(2n 1) (2n 1)!

2. Розкласти задані функції по степенях х за допомогою формули Маклорена:

В 1.

f (x)

ex

1

,

В 2.

f (x)

sin

x

,

В 3.

f (x)

sin2 x

x

2

В 4.

f (x)

x ln(1

x2 ) , В 5. f (x)

1

x2 ,

В 6.

f (x)

3 8

x3

Питання для самоконтролю

1.Сформулювати та довести такі достатні ознаки збіжності: ознаки порівняння, граничну ознаку порівняння; ознаки Д‟Аламбера і Коші; інтегральну ознаку Коші. Для яких рядів застосовані ці ознаки?

2.Сформулювати та довести ознаку Лейбниця. Для якого ряду застосована ця ознака?

3.Чому не можна досліджувати за ознакою Лейбниця на збіжність ряд.

n 1

n 1

un

n 1 * 2n

1

Lim

1

Lim

2n 1

Lim

Lim

n n

un

n

n * 2

n 1

n

2

n

n

n

n

2

2n

n

4.У чому полягає наслідок із ознаки Лейбниця?

5.Сформулювати та довести достатню ознаку збіжності знакозмінного ряду.

6.Дайте визначення степеневого ряду.

7.Сформулюйте теорему збіжності степеневого ряду (теорема Абеля)

8.Як знайти радіус збіжності степеневого ряду.

9.Які властивості степеневого ряду?

10.Теорема про єдиність розкладу функцій в степеневі ряди.

11.Запишіть формулу Маклорена.

12.Запишіть формулу Тейлора.

13. Розкладання елементарних функцій в ряди Маклорена.

Література [1,2,4]

ПРАКТИЧНЕ ЗАНЯТТЯ № 34 Тема 15. Елементи фінансової математики та математичної економіки

Мета заняття. Вивчення теми надасть студентам можливість опанувати прості і складні відсотки у фінансових розрахунках, вивчити поняття необхідної відсоткової ставки, дисконтування, неперервних відсотків. Зокрема,

еквівалентність простих і складних відсотків, розрахунок номінальної ставки і ставки ефективності.

План заняття

1.Формула нарощування за простими процентами.

2.Формула нарощування за складними відсотками.

3.Дисконтування та облік.

4.Номінальна і ефективна ставки процентів.

5.Нарахування процентів в умовах інфляції.

6.Фінансові ренти.

Методичні рекомендації до практичного заняття

Формула нарощування за простими процентами Під нарощеною сумою суди 9боргу, депозиту) розуміють її початкову суму

разом із нарахованими на неї відсотками к кінцю строку. Нехай P - початкова сума грошей, i - ставка простих процентів, тоді формула нарощування за простими процентами за n періодів запишеться у вигляді:

S P(1 ni) .

Процентні ставки не залишаються незмінними в часі, тому в кредитних угодах іноді передбачають дискретно змінні в часі процентні ставки. В цьому випадку формула розрахунку нарощеної суми має вигляд:

m

S P(1 ntit ) ,

t 1

де P		- початкова сума грошей, it	- ставка простих процентів в періоді з номером
t	1, m	, n - тривалість t періоду нарахування за ставкою it .
		Дисконтування та облік
		На практиці часто доводиться розв‟язувати задачу, обернену нарощуванню
відсотків, коли по заданій сумі			S , що	відповідає кінцю фінансової операції,
потрібно знайти початкову суму			P , цей розрахунок називають дисконтуванням
суми		S . Проценти у вигляді різниці		D S P називаються дисконтом, або

знижкою. Процес нарахування або утримання процентів наперед називають

обліком.

Формула дисконтування:

P S(1 in) ,

де вираз 1(1 in) називається дисконтним множником.

При розрахунку процентів при обліку векселів застосовується облікова

ставка, яку позначають d .

Проста річна облікова ставка знаходиться за формулою

d (S P)Sn .

Розмір дисконту, або облік, що утримується банком,

D Snd .

Складні проценти

Формула нарощування за складними процентами Складні проценти застосовуються в довгострокових фінансово-кредитних

операціях, якщо проценти на сплачуються періодично відразу після їх нарахування за минувший період часу, а додаються до суми боргу. Приєднання нарахованих процентів до суми, яка була базовою для їх нарахування, називають капіталізацією

процентів. Нехай початкова сума боргу дорівнює P ,		S - нарощена сума, i - річна
ставка складних процентів; n - термін суди, тоді
S	P(1 i)n .
Втому випадку, коли ставка складних процентів змінюється в часі, формула
нарощування набуває вигляду:
S P(1 i )n1	(1 i )n2 .....(1	i )nk ,
1	2	k

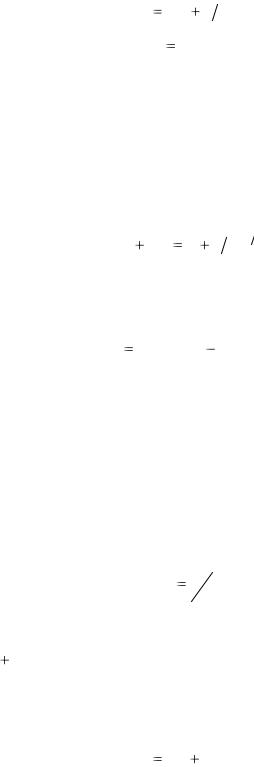
де i1,i2 ,..., ik - послідовність значень ставок процентів, що діють в періоди n1, n2 ,..., nk

відповідно.

Номінальна та ефективна ставки процентів та їх облік

Означення. Нехай річна ставка складних відсотків дорівнює j , а число періодів нарахування протягом ріку m . Тоді щоразу проценти нараховуються за ставкою j 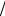m . Ставка j називається номінальною. Нарахування процентів за номінальною ставкою відбувається за формулою

S	P(1 j m)S ,
де N - кількість періодів нарахування, N	mn .

Означення. Ефективна ставка показує, яка річна ставка складних процентів

дає той самий фінансовий результат, що і m - разове нарощування в рік за ставкою

j 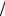m .

Якщо проценти капіталізуються m раз на рік, кожного разу за ставкою j 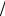m ,

то можна записати рівність для відповідних множників нарощування:

(1 i )n	(1 j m)m n ,
e

де ie - ефективна ставка, а j - номінальна ставка. Звідси отримаємо, що зв‟язок між ефективною і номінальною ставками виражається співвідношенням

ie (1jm)m 1.

Нарахування процентів в умовах інфляції Нарахування за простими процентами

Якщо нарощення за n років сума грошей складає S , а індекс цін дорівнює JP

, то реально нарощена сума грошей з урахуванням їх покупної спроможності складає

C S J	.
	P
Нехай очікуваний середній річний темп інфляції дорівнює h . Тоді річний
індекс цін складає (1 h) .

Якщо нарощування відбувається за простою ставкою протягом n років, то реальне нарощування при темпі інфляції h складає

C P(1 ni)JP ,

де в загальному випадку

n

JP (1 ht ) .

t 1

Нарахування за складними процентами Нарощення за складними процентами сума до кінця строку суди з

урахуванням падіння покупної спроможності грошей складає

C

P(1 i)n

,

J

P

n

де індекс

цін визначається виразом

JP

(1

ht ) .

В цьому

випадку

падіння

t 1

покупної

спроможності грошей компенсується

при

ставці i

h ,

яка забезпечує

рівність C

P .

Фінансові ренти

Означення. Потік платежів, всі члени якого додатні величини, а часові

інтервали постійні, називають фінансовою рентою.

Нехай наприкінці кожного року протягом n

років на розрахунковий рахунок

вноситься по R грошових одиниць, проценти нараховуються один раз на рік за

ставкою i . Наприкінці строку ренти її нарощена сума буде дорівнювати:

S

R

(1

i)n

1

.

i

Знайдемо нарощену суму за умови, що рента сплачується

p раз

на рік

рівними платежами, а проценти нараховуються один раз наприкінці року.

Якщо R - річна сума платежів,

то розмір окремого платежу дорівнює R p .

Тоді нарощена сума обчислюється за формулою:

S

R

(1

i)n

1

.

p (1

i)1| p

1

Приклади

1. Нехай фірмою взято в банку кредит у розмірі 100 тис. грн. на строк 3 роки.

Річна декурсивна ставка відсотків – 14%. Обчислити за формулою розрахунку простих відсотків суму відсоткових грошей та кінцеву суму боргу.