Математика для економістів Ден.. 2010 ч

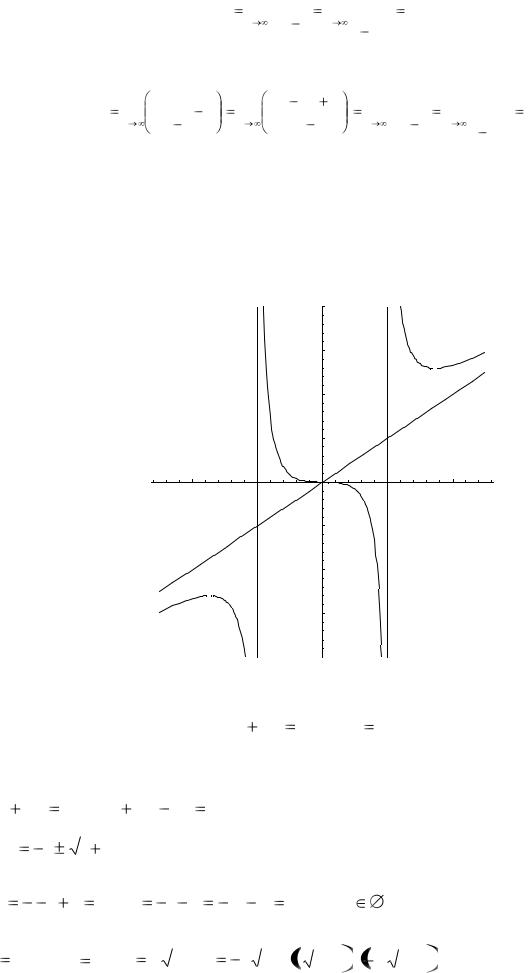
k

lim

x 2

lim

1

1;

x

2

1

1

x

x

1

x 2

1

x3

x3

x3

x

x

b lim

x

lim

lim

lim

x

0 .

x

2

x

2

1

x

2

1

1

x

1

x

x

x

1

x 2

Отримали рівняння похилої асимптоти – y=x.

Побудуємо графік функції:

		4
		3
		2
		1
- 2	- 1	1	2
		- 1
		- 2
		- 3
		- 4

7. Знайти кути перетину ліній:

															x	2			y	2		24 та y					1		x		2	.
																										2
Розв'язок. Знаходимо точки перетину ліній:
2 y y2				24 , y2							2 y 24 0 ,
y1			1			1	24 ,
12
y				1 5 4 ,				y				1 5 6					,	6			1	x	2		x	.
										2
1																					2
4	1	x	2		2
				, x		8	,	x				2 2 , x			2		2	2 ,			2		2,4 ,			2				2,4 – точки перетину ліній.
	2							1

Для першої лінії:

2x 2yy 0 ,

y			2x											x			,
		2 y												y
																					2							2											2							,
k		y 2			2,4
1																					4																		2
																					2							2											2				.
k		y			2			2,4
1																					4																		2
Для другої лінії:
y		x ,
k2		y 2 2 2 2 , k2																																					y					2 2								2 2 .
Кут між кривими знаходиться за формулою
tg			k2					k1							, tg																				k2						k1						,
																					1
	1				k2k1																							1										k2						k1
																					2
					2			2
																																			4				2					2								5		2								5	2
tg																				2																																							,		arctg				.
	1																																						2 1					2										2						1		2
																					2
	1				2			2
																				2

tg

tg

			k2		k1				,
2	1		k2		k1
									2
			2	2
																4				2	2		5			2		5				2					5	2
									2																									,		arctg					.
2																2 1					2					2					2				2			2
										2
	1			2			2
									2
	8.		Замінивши приріст функції диференціалом,																																	знайти наближено значення

arctg(1,05).
Розв'язок. Нехай f ( x)			arctg x, тоді маємо
arctg(x	x)	arctg x	(arctg x) x;
arctg(x	x)	arctg x	x	.
			1 x 2
Якщо x	1,	x 0,5, то arctg1,05 arctg1			0,5			0,025 0,811.
					2		4

9. Знайти екстремум функції:

y

x3 3x 9x 1.

Розв'язок. Знайдемо похідну і прирівняємо її до нуля:

y

3x2

6x

9

0 ,

x1

1 та x2

3

y 6x 6 , y 1

6 6 12 0, y 3 18 6 12 0

ymax

y

1

1

3

9 1

6 , ymin

y 3

27 27

27

1

26 .

Знайти найбільше й найменше значення функції y 2e3

10.

x2

на сегменті

[ 8,

8] .

3

4e

x2

Розв'язування. Функція неперервна на сегменті. Похідна функції

y

не

33

x

дорівнює нулю на інтервалі (

8,

8) , але в точці

x

0

її не існує. Це критична

точка функції y

2e3 x2 . При переході через цю точку зліва направо похідна змінює

знак

із мінуса

на

плюс,

тому

функція

в точці

x

0

має

мінімум.

Так

як на

розглянутому сегменті у функції існує єдиний екстремум–мінімум, то знайдений мінімум і є найменшим значенням функції на сегменті. Це найменше значення

дорівнює 2,	найбільше значення функції – 2e2 досягається в кінцевих точках
сегмента: x1		8 , x2		8 .
					Завдання

Дослідити функції на екстремум і побудувати їх графіки:

В.1

y

2

В.2

y

x

2

x

2

4

x

4

В.3

y

x2

1

В.4

y

2x2

x 3

x

6

2x

3

x

1

3

В.5

y

В.6

y x ln x

x

1

Питання для самоконтролю

8.Яка функція називається неперервною в точці?

9.Яка функція називається неперервною на відрізку?

10.Сформулювати властивості неперервних функцій.

11.Що називається асимптотою функції, Якими бувають асимптоти?

12.Сформулювати необхідну і достатні умови існування екстремуму функції однієї змінної.

13.Викласти схему дослідження функцій.

14.Як визначити найменше та найбільше значення функції на відрізку?

Література [1,2,4]

ПРАКТИЧНЕ ЗАНЯТТЯ № 13

Тема 8. Граничний (маргінальний) аналіз

Мета заняття. Вивчення теми надасть студентам можливість знати застосування похідної в економіці, такі граничні показники в мікроекономіці, як гранична собівартість продукції, граничний дохід, граничні витрати, гранична продуктивність праці і т.п., також гранична схильність до споживання та збереження в макроекономічній моделі національного доходу. А також еластичність економічних показників.

План заняття

1.Граничні показники в мікроекономіці.

2.Еластичність економічних показників.

3.Максимізація прибутку.

Методичні рекомендації до практичного заняття

Граничні показники в економіці Розглянемо два граничних показники в економіці: гранична собівартість та

граничні витрати.

Перший з них пов‟язаний із залежністю собівартості С виготовленої

продукції від її обсягу Q :				C f (Q). Так звана гранична собівартість характеризує
собівартість C приросту продукції Q :
MC		C	.
		Q
В припущенні	про			неперервну залежність C від Q доцільна заміна

різницевого відношення його границею:

	MC lim	C	C'(Q) .
		Q
	Q 0

Зазвичай, під граничною собівартістю розуміють саме цю величину (див.

Приклад 1).

Еластичність економічних показників В аналізі і прогнозах цінової політики застосовується поняття еластичності

попиту. Нехай D f (P) - функція попиту від ціни товару P . Тоді під еластичністю попиту розуміють процентну зміну попиту при зміні ціни товару на один процент:

		E		D D 100%				.
					P P	100%
	У випадку неперервної залежності				P від Q зручно перейти до границі при
	P 0 :
		E(D)			P	D'(P)	.
						D(P)
	Аналогічне поняття можна вивести і для функції пропозиції S(P) . Зазначимо,
	що функція D(P) спадна, а функція S(P)			зростає з ростом ціни P .
	Властивості	еластичності. Формулу				E(D)			P	D'(P)	можна виразити
										D(P)
	наступним чином:
		E(D)			P(lnD(P))' .
	З останньої рівності слідує, що E(D)				має властивості логарифма, а отже,
		E(D1D2 ) E(D1) E(D2 ) , E(D1 D2 )							E(D1) E(D2 ) .
	Відмітимо, що	оскільки функція D(P) спадна, то D'(P)									0, а тоді, відповідно,

іE(P) 0 . Навпаки, оскільки функція пропозиції зростаюча, то відповідна

еластичність E(S) 0 .
Можливі такі випадки:
а) якщо | E(D) |	1 ( E(D)	1), то попит вважається еластичним;
б) якщо | E(D) |	1 ( E(D)	1), то попит нейтральний4
в) якщо | E(D) |	1 ( E(D)	1), то попит не еластичний (див. приклад 3).
Поняття еластичності		розповсюджується на інші області економіки
(наприклад див. приклад 4).

Максимізація прибутку

Нехай Q кількість реалізованої продукції, R(Q) - функція прибутку, C(Q) -

функція витрат на виробництво продукції. В реальності вигляд цих двох функцій залежить в першу чергу від способу виробництва, організації інфраструктури і т.п.

Прибуток від реалізації виготовленої продукції знаходимо за формулою:

(Q) R(Q) C(Q) .

В мікроекономіці відоме твердження: для того, щоб прибуток був максимальним, необхідно, щоб граничний прибуток і граничні витрати були рівними. Цей принцип можна записати наступним чином:

R'(Q) C(Q) .

Приклади

1. Нехай залежність витрат виробництва від обсягу виробляємої продукції виражається формулою:

C 20Q 0,05Q3

грошових одиниць. Визначити середні і граничні витрати при обсязі продукції

вартістю Q 10 грошових одиниць.

Розв'язок. Функція середніх витрат на одиницю продукції визначається за

формулою					C / Q , або в нашому випадку,
			C
										20 0,05Q2 ,
								C
звідки		(10)					0,05 102 15 грошових одиниць.
	C				20
Граничні витрати визначаються за формулою
MC lim							C	C'(Q) , отже C'(Q) 20 0,015Q2 ,
							Q
			Q		0
звідки при Q					10 отримаємо C'(10)					5 грошових одиниць.

Іншими словами, при середніх витратах на виробництво одиниці продукції в 15 г.

о. додаткові витрати на виробництво одиниці додаткової продукції становлять 5 г.

о. і не перевищують середніх витрат.

2. Нехай попит на товар визначається формулою

D(P) 100 3P .

Знайти еластичність попиту при ціні на товар P 20 г. о.

	Розв'язок. Відповідно до формули E(D) P	D'(P)	маємо:
		D(P)
	E(D) 20 ( 3) (100 3		20) =-1,5.

Це означає, що при збільшенні (зменшенні) ціни товару на 1% попит на нього зменшиться (збільшиться) на 1,5%.

3. Знайти зміну виручки із збільшенням ціни товару при різних варіантах еластичності попиту.

Розв'язок. Виручка I дорівнює добутку ціни P товару на величину попиту D :

I (P) D(P) P .

Знайдемо похідну цієї функції:

I '(P) D(P) P D'(P) .

Проаналізуємо усі варіанти еластичності попиту, наведені раніше.

	1. E(D) 1	: тоді, підставляючи E(D) P	D'(P)	в нерівність, отримаємо, що права
			D(P)

частина рівняння I '(P) D(P) P D'(P) від‟ємна. Таким чином, при еластичності попиту підвищення ціни P приводить до зниження виручки. Навпаки, зниження ціни товару збільшує виручку.

2.

E(D)

1:

із рівності

E(D)

P

D'(P)

слідує,

що

права

частина

D(P)

I '(P) D(P)

P D'(P) дорівнює нулю,

тобто при нейтральному попиті зміна ціни

товару не впливає на виручку.

3.

E(D) 1:

тоді

I '(P) 0 , тобто при не еластичному попиті збільшення ціни

P

товару приводить до збільшення виручки.

4. Нехай залежність між собівартістю

продукції

C

і обсягом Q

її

виробництва виражається формулою:

C 50 0,5Q .

Необхідно визначити еластичність собівартості при випуску продукції Q

30.

Розв'язок. За формулою E(C)

Q

C'(Q)

отримаємо:

C(Q)

E(C)

0,5Q

,

50 0,5Q

звідки при Q 30 шукана еластичність складає приблизно -0,42, тобто збільшення

даного обсягу випуску продукції на 1% призведе до зниження його собівартості приблизно на 0,42%.

Завдання

1. Функція попиту має вигляд: D(P) D0 exp( kP2 ) , де D0 , k - відомі величини.

Знайти, за яких значень ціни попит буде еластичним.

2. Залежність між собівартістю продукції С та об'ємом її виробництва задана формулою: C 50 0,4Q . Треба визначити еластичність собівартості при Q = 30

грош. од.

3. Нехай функції доходу і витрат відповідно мають вигляд:

R(Q) 100Q Q 2 ; C(Q) Q3 37Q 2 169Q 4000. Знайти максимальний прибуток.

4. Нехай в короткотерміновому плані виробнича функція залежить тільки від кількості персоналу фірми та має вигляд: Q 6L2 0,2L3 , де Q – випуск продукції, L

– кількість працівників. Визначити численність персоналу, за якої випуск є максимальним.

Питання для самоконтролю

1.Поясніть економічний зміст похідної.

2.Наведіть приклади застосування похідної в економіці.

3.Поясніть , що таке граничні показники в економіці. Наведіть приклади.

4.Сформулюйте задачі на визначення оптимального розв'язку: максимум прибутку, оптимізація оподаткування і т. ін.

Література [1,2,4]

Модуль І. Вища математика

Змістовий модуль ІІІ. Диференціальне числення функції багатьох змінних та

його застосування в економіці

ПРАКТИЧНЕ ЗАНЯТТЯ № 14

Тема 9. Основні поняття функції багатьох змінних та їх інтерпретація в

економічній теорії

Тема 10. Диференційованість функцій багатьох змінних

Мета заняття. Вивчення теми надасть студентам можливість знати поняття функції багатьох змінних, області визначення функції. Також,

ознайомитись з економічною інтерпретацією функції багатьох змінних: функція корисності, виробничі функції. Набути навички обчислення частинних похідних,

повної похідної, Повного диференціала та застосування повного диференціала в наближених обчисленнях.

План заняття

1.Означення функції багатьох змінних.

2.Область визначення функції багатьох змінних.

3.Частинні похідні і диференціали функції багатьох змінних.

4.Виробнича функція, функція корисності.

5.Частинні похідні функції багатьох змінних.

6.Повний диференціал першого порядку.

7.Застосування повного диференціалу в наближених обчисленнях.

Методичні рекомендації до практичного заняття

Функції багатьох змінних

При вивченні функцій багатьох змінних обмежимось детальним дослідженням функцій двох змінних, так як всі отримані результати будуть справедливими для функцій довільного числа змінних.

Означення. Якщо кожній парі незалежних один від одного чисел (х,у) із деякої множини за будь-яким правилом ставиться у відповідність одне або декілька значень змінної z, то змінна z називається функцією двох змінних:

z = f(x,y).

Означення. Якщо парі чисел (х,у) відповідає одне значення z, то функція називається однозначною, а якщо більш одного, то – багатозначною.

Означення. Областю визначення функції z називається сукупність пар (х,у),

при яких функція z існує.

Означення. Околом точки М0(х0, у0) радіуса r називається сукупність всіх

точок (х,у), які задовольняють умові	2	y y0	2	r .
	x x0

Означення. Число А називається границею функції f(x, y) при прямуванні точки М(х, у) до точки М0(х0, у0), якщо для кожного числа >0 знайдеться таке число r>0, що для будь-якої точки М(х, у), для яких виконується умова:

MM 0 r

також виконується і умова:	f (x, y) A	.
Записують: lim f (x, y) A

xx0

yy0

Означення. Нехай точка М0(х0, у0) належить області визначення функції f(x, y). Тоді функція z=f(x,y) називається неперервною в точці М0(х0, у0), якщо

lim f (x, y) f (x0 , y0 )
x	x0
y	y0

причому точка М(х,у) прямує до точки М0(х0, у0) довільним чином.

Якщо в деякій точці ця умова не виконується, то ця точка називається

точкою розриву функції f(x,y). Це може бути в наступних випадках: 1) Функція z = f(x, y) не визначена в точці М0(х0, у0).

2) Не існує границя lim f (x, y) .

xx0

yy0

3)Ця границя існує, але вона не дорівнює f(x0,y0).

Властивість. Якщо функція f(x, y, …) визначена і неперервна в замкнутій і обмеженій області D, то в цій області знайдеться принаймні одна точка N(x0, y0, …),

така, що для інших точок виконується нерівність

f(x0, y0, …) f(x, y, …),

а також точка N1(x01, y01, …), така, що для всіх інших точок виконується нерівність f(x01, y01, …) f(x, y, …)

тоді f(x0, y0, …)=M – найбільше значення функції, а f(x01, y01, …)=m – найменше значення функції f(x, y, …) в області D.