Математика для економістів Ден.. 2010 ч

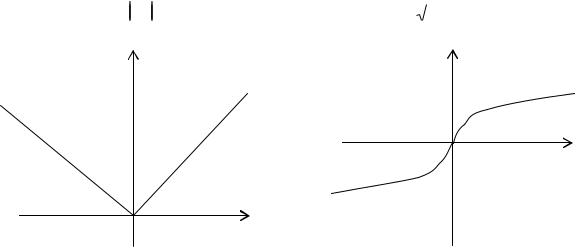
Теорема. (необхідна умова існування екстремуму). Якщо функція f(x)

диференційована в точці х = х1 і точка х1 є точкою екстремуму, то похідна функції обертається в нуль в цій точці.

Наслідок. Обернене твердження невірне. Якщо похідна функції в деякій точці дорівнює нулю, то це ще не значить, що в цій точці функція має екстремум.

Приклад цього – функція у = х3, похідна якої в точці х=0 дорівнює нулю, однак в цій точці функція має лише перегин, а не максимум або мінімум.

Означення. Критичними точками функції називаються точки, в яких похідна функції не існує або дорівнює нулю.

Розглянута теорема дає нам необхідні умови існування екстремуму, але цього недостатньо.

Приклад: f(x) = x
	Приклад: f(x) = 3 х
y		y

x

х
В точці х=0 функція має мінімум,	В точці х=0 функція не має ні
але не має похідної.	максимуму, ні мінімуму, ні
	похідної.

Взагалі кажучи, функція f(x) може мати екстремум в точках, де похідна не існує або дорівнює нулю.

Теорема. (Достатні умови існування екстремуму). Нехай функція f(x)

неперервна в інтервалі (a, b), який містить критичну точку х1, і диференційована в усіх точках цього інтервалу (окрім, можливо, самої точки х1).

Якщо при переході через точку х1 зліва направо похідна функції f (x) змінює знак з “+” на “-“, то в точці х = х1 функція f(x) має максимум, а якщо похідна змінює знак з “-“ на “+”- то функція має мінімум.

Найбільше та найменше значення функції на відрізку

На основі вищесказаного можна встановити єдиний порядок дій при знаходженні найбільшого і найменшого значення функції на відрізку:

1)Знайти критичні точки функції.

2)Знайти значення функції в критичних точках.

3)Знайти значення функції на кінцях відрізка.

4)Вибрати серед отриманих значень найбільше і найменше.

Дослідження функції на екстремум за допомогою похідних вищих порядків

Нехай в точці х=х1 f (x1)=0 і f(x1) існує і неперервна в деякому околі точки

х1.

Теорема. Якщо f (x1) = 0, то функція f(x) в точці х=х1 має максимум, якщо f(x1)<0 і мінімум, якщо f(x1)>0.

Якщо f(x)=0, то характер критичної точки невідомий. Для його визначення потрібне подальше дослідження.

Опуклість і вгнутість кривої.

Точки перегину.

Означення. Крива обернена опуклістю вгору на інтервалі (а,b), якщо всі її точки лежать нижче будь-якої її дотичної на цьому інтервалі. Крива, обернена опуклістю вгору, називається опуклою, а крива, обернена опуклістю вниз – називається вгнутою.

На рисунку показана ілюстрація наведеного означення.

у

x

Теорема 1. Якщо в усіх точках інтервалу (a, b) друга похідна функції f(x)

від’ємна, то крива y = f(x) обернена опуклістю вгору (опукла).

Означення. Точка, відтинаюча опуклу частину кривої від вгнутої,

називається точкою перегину.

В точці перегину дотична перетинає криву.

Теорема 2. Нехай крива визначається рівнянням y=f(x). Якщо друга похідна f(a)=0 або f(a) не існує і при переході через точку х=а f(x) змінює знак, то точка кривої з абсцисою х=а є точкою перегину.

Асимптоти

При дослідженні функцій часто буває, що при віддаленні координати х точки кривої у нескінченність крива необмежено наближається до деякої прямої.

Означення. Пряма називається асимптотою кривої, якщо відстань від змінної точки кривої до цієї прямої при віддаленні точки у нескінченність прямує до нуля.

Необхідно зазначити, що не кожна крива має асимптоту. Асимптоти можуть бути прямі і похилі. Дослідження функцій на наявність асимптот має велике значення і дозволяє більш точно визначати характер функції і поведінку графіка кривої.

	В загалі кажучи, крива, необмежено наближаючись до своєї асимптоти, може
і	перетинати її, причому не в			одній	точці,	як показано	на	наведеному нижче
			x
графіку функції y		x	e 3 sin x . Її похила асимптота у=х.
					10
					5
	- 10		- 5			5		10
					- 5
					- 10
					- 15
					- 20
			Вертикальні асимптоти

	Із означення асимптоти слідує, що якщо lim						f (x)	або lim	f (x)	або
						x a 0		x a 0
lim f (x)		, то пряма х=а – асимптота кривої y=f(x).
x a
	Наприклад, для функції f (x)				2	пряма х=5 є вертикальною асимптотою.
				x		5
				Похилі асимптоти
	Припустимо, що крива y=f(x) має похилу асимптоту y=kx+b.
				15
				12. 5
				10
				7. 5
				5
				2. 5
						1	2	3		4
Тоді	lim[ f (x)		(kx b)]	0 .
	x
Для точного визначення прямої y=kx+b необхідно знайти спосіб обчислення
коефіцієнтів k і b.

У виразі lim[ f (x) (kx b)] 0 виносимо за дужки х:

x

lim x

f (x)

k

b

0

x

x

x

Так як х

, то lim

f (x)

k

b

0 , так як b=const, то

x

x

x

lim

b

0;

limk

k .

x

x

x

Тоді lim

f (x)

k

0

0 ,

отже,

x

x

k

lim

f (x)

.

x

x

Так як lim f (x)

(kx

b)

0 , то

lim f (x)

kx

limb

0 , отже,

x

x

x

b lim f (x) kx .

x

Горизонтальні асимптоти

Якщо в рівнянні похилої асимптоти y=kx+b функції y=f(x) маємо k =0, то таку похилу асимптоту називають горизонтальною асимптотою функції. Отже,

горизонтальна асимптота – частинний випадок похилої – відшукується як похила асимптота за умов

k

lim

f (x)

0 , b

lim f (x) kx

lim f (x)

x

x

x

x

і має вигляд y

b . До речі, умову lim

f (x)

0 можна не перевіряти, якщо b

lim f (x)

x

x

x

-

скінчена границя, оскільки в такому разі границя

k lim

f (x)

завжди дорівнює

x

x

нулю. Звідси можна зробити висновок:

Для того що пряма y b була горизонтальною асимптотою функції y=f(x),

x

(a;

) , x

(

; a) ,

необхідно і

достатньо, щоб

існувала

скінчена

границя

b lim f (x) .

x

Загальний план дослідження функції Процес дослідження функції складається із декількох етапів. Для найбільш

повного уявлення про поведінку функції і характер її графіка необхідно визначити:

1) Область існування функції.

Це поняття включає в себе і область значень і область визначення функції.

2)Дослідити функцію на парність, непарність, періодичність.

3)З‟ясувати точки перетину функції з осями координат.

4)Дослідити функцію на неперервність. Встановити точки розриву (якщо вони є).

5)Визначити інтервали зростання і спадання функції.

6)Знайти точки максимуму і мінімуму та значення функції в цих точках.

7)Знайти максимальне і мінімальне значення функції на її області визначення (якщо вони існують).

8)Визначити області опуклості і вгнутості, а також точки перегину функції.

9)Знайти асимптоти графіка функції (якщо вони існують).

10)Побудувати графік функції.

Застосування цієї схеми розглянемо на прикладі (див. приклад 6).

				Приклади
1. Функція f(x)=	1	має в точці х0=0 точку розриву 2 – го роду, так як
	х
		lim f (x)		;	lim			f (x)	.
		x	0 0		x	0	0
				7.5
					5
				2.5
		-10	-5					5	10
				-2.5
				-5
				-7.5

2. Дослідити функцію на неперервність f(x) =	sin x	.
	x

Функція не визначена в точці х=0, але має в ній скінчену границю lim f (x) 1 , тобто

x 0

в точці х=0 функція має точку розриву 1–го роду. Це – усувна точка розриву, так як якщо довизначити функцію:

	sin x			,	при	x 0 .
f (x)		x
1,			при		x	0

Графік цієї функції:

		1
	0.	8
	0.	6
	0.	4
	0.	2
- 20	- 10	10	20
	- 0. 2

3. Знайти асимптоти і побудувати графік функції y

x2

2x 1

.

x

1) Вертикальні асимптоти: y +

при

x

0-0; y

-

при x

0+0, отже, х= 0-

вертикальна асимптота.

2) Похилі асимптоти:

k

lim

x 2

2x 1

lim 1

2

1

1

x

2

x

x

2

x

x

b lim( f (x) x)

lim

x2

2x 1

x

lim

x2

2x 1 x2

lim

2x 1

lim 2

1

2

x

x

x

x

x

x

x

x

x

Таким чином, пряма у=х+2 є похилою асимптотою.

Побудуємо графік функції:

		6
		4
		2
- 3	- 2	- 1		1	2	3
		- 2
				9x
4. Знайти асимптоти і побудувати графік функції y			9	x 2 .
Прямі х = 3 і х = -3 є вертикальними асимптотами кривої.

Знайдемо похилі асимптоти: k

lim

9

0 ;

9

x

2

x

9

9x

b

lim

lim

x

0

;

9

x

2

9

x

x

1

x 2

Отже, y=0 – горизонтальна асимптота.

Побудуємо графік цієї функції.

6

4

2

- 7. 5

- 5

- 2. 5

2. 5

5

7. 5

- 2

- 4

- 6

	5. Знайти асимптоти і побудувати графік функції y	x2	2x 3	.
		x	2

Пряма х=-2 є вертикальною асимптотою кривої.

Знайдемо похилі асимптоти:

1

2

3

x 2

2x 3

x 2

2x 3

x

x 2

k lim

lim

lim

1.

x(x

2)

x

2

2x

2

x

x

x

1

x

4

3

b

lim

x 2

2x 3

x

lim

x 2

2x 3 x 2

2x

lim

4x 3

lim

x

4

x

2

x

2

x

2

2

x

x

x

x

1

x

Отже, пряма у = х – 4 є похилою асимптотою.

Графік функції:

20

15

10

5

- 10

- 5

5

10

- 5

- 10

- 15

- 20

x3

6. Дослідити функцію y

x2

1 і побудувати її графік.

Знаходимо область існування функції. Очевидно, що областю визначення

функції є область (- ; -1)

(-1; 1)

(1;

).

Також є очевидним, що прямі х=1, х=-1 являються вертикальними

асимптотами кривої.

Областю значень даної функції є інтервал (- ; ).

Точками розриву функції є точки х = 1, х = -1.

Знаходимо критичні точки.

Знайдемо похідну функції

y	3x2 (x2	1) 2x x3		3x4 3x2 2x4		x4	3x2	.
	(x2	1)2		(x2 1)2		(x2	1)2

Критичні точки: x = 0; x = - 3 ; x = 3 ; x = -1; x = 1.

Знаходимо проміжки зростання і спадання функції. Для цього визначаємо знаки похідної функції в проміжках:

- < x < - 3 , y> 0, функція зростає

- 3 < x < -1,

y

< 0,

функція спадає

-1 < x < 0,

y < 0,

функція спадає

0 < x < 1,

y < 0,

функція спадає

1 < x <

3 ,

y < 0,

функція спадає

3 < x <

,

y

> 0, функція зростає.

Видно, що точка х=-

3 є точкою максимуму,

а точка х= 3 є точкою мінімуму.

Значення функції в цих точках дорівнюють відповідно -3 3 /2 і 3

3 /2.

Обчислимо другу похідну функції

y

(4x3

6x)(x2

1)2

(x4

3x2 )4x(x2

1)

(x2

1)4

(4x3

6x)(x4

2x2

1)

(x4

3x2 )(4x3

4x)

(x2

1)4

4x7

8x5

4x3

6x5

12x3

6x 4x7

4x5

12x5

12x3

(x2

1)4

2x5

4x3

6x

2x(x4

2x2

3)

2x(x2

3)(x2

1)

2x(x2

3)

.

(x2

1)4

(x2

1)4

(x2

1)4

(x2

1)3

Визначимо опуклість і вгнутість кривої на проміжках.

-< x < - 3 , y< 0, крива опукла

-3 < x < -1, y< 0, крива опукла

-1 < x < 0,					y	> 0, крива вгнута
0	< x < 1,				y	< 0,	крива опукла
1	< x <		3 ,		y	> 0,	крива вгнута
	3 < x <		,		y	> 0,	крива вгнута

Про вертикальні асимптоти було вже сказано вище. Тепер знайдемо похилі асимптоти: