geometry24

ЛЕКЦИЯ16.ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

§54.Поверхности второго порядка

Поверхности второго порядка задаются в некоторой аффиной системе координат уравнением

F (x, y, z) = a|11x2 + a22y2 + a33z2 +{z2a12xy + 2a13xz + 2a23yz} +

q(x,y,z)

квадратичная часть

+	2a1x + 2a2y + 2a3z					+a0 = 0	(54.1)
	|		{z		}

l(x,y,z)

однородная линейная часть

При этом требуется,чтобы квадратичная часть была отлична от нуля,т.е.хотя бы одно из чисел a11, a12, a13, a22, a23, a33 было ненулевым.Если ввести обозначения

a11

a12

a13

a11

a12

a13

a1

x

@

A

0 a12

a22

a23

a2

1

@

A

Q =

a12

a22

a23

, A =

, L = (a1, a2

, a3), X =

y

,

B

1

2

3

0

C

0

1

@

a13

a23

a33

a3

A

0 1

a13 a23

a33

B a

a

a a

C

z

то уравнение примет вид

B

x

C

1

XT QX + 2LX + a0 = (x, y, z, 1)A

B

C

= 0.

(54.2)

0 y

1

@

z

A

Как и раньше,будем называть квадрикой многочлен второй степени с точностью до умножения на ненулевой множитель.

Пока будем считать систему координат прямоугольной.

Лемма54.1. Все собственные числа матрицы Q вещественные,а собственные векторы,принадлежащие различным собственным числам,ортогональные.

Доказательство. Заметим,что матрица Q симметричная: QT = Q.Кроме того, если комплексное число λ = + iβ (β 6= 0) является корнем ее характеристического

полинома,то и комплексно-сопряженное число			¯	также является корнем ее
			λ = −iβ
характеристического полинома.Это следует из того,что				χQ(λ) полином с веще-
ственными коэффициентами.
	x1
Пусть X =	0 x2 1	собственный вектор,принадлежащий собственному числу

x3
λ.Тогда X¯ @векторAс комплексно-сопряженными компонентами собственный
				¯				¯ T	QX .
вектор,принадлежащий собственному числу λ.Рассмотрим число								X
С одной стороны,оно равно
¯ T		¯ T		¯ T		¯ ¯ T	X,
X	QX = (X		Q)X = (QX)		X = λX
а с другой стороны	¯ T		¯ T		¯ T
						X.
	X	QX = X		(QX) = λX

101

Отсюда,учитывая то,что	X	X = |x1|		+|x2|			+|x3|		6= 0,так как вектор X нену-
	¯ T		2			2		2
левой(это собственный вектор),получаем,что							¯
					λ = λ,т.е. β = 0 и λ вещественное
число.
Доказательство ортогональности собственных векторов,принадлежащих раз-
личным собственным числам матрицы Q,в точности повторяет доказательство для
случая кривых,когда матрица	Q симметричная матрица второго порядка.

Лемма54.2. Произведение двух ортогональных матриц ортогональная матрица.

Доказательство. Пусть C1 и C2 ортогональные матрицы,т.е. C1T C1 = E , C2T C2 = E .Рассмотрим матрицу C1C2 .Имеем

(C1C2)T (C1C2) = C2T (C1T C1)C2 = C2T EC2 = E,

следовательно,матрица C1C2 ортогональная.

Теорема54.1. Существует прямоугольная система координат,в которой уравнение поверхности второго порядка имеет вид

F 0(x0, y0, z0) = λ1x02 + λ2y02 + λ3z02 + 2b1x0 + 2b2y0 + 2b3z0 + b0 = 0.

Доказательство. Пусть λ1 собственное число матрицы Q,отличное от остальных собственных чисел λ2, λ3 а X1 вещественный собственный вектор,принадлежащий данному собственному числу.Мы можем выбрать X1 так,чтобы его длина была равна 1.Выберем в пространстве ортонормированный базис так,что i = X1, j, k (мы будем считать,что координаты векторов записываются по столбцам).

Рассмотрим,как изменится квадратичная часть уравнения поверхности при пе-

реходе к этому базису.

X1T

A

X1T

A

@ kT

@ kT

Q0 = 0

jT

1 Q(X1, j, k) = 0

jT

1 (QX1, Qj, Qk) =

XT

1

0

λ1XT X1

XT Qj XT Qk

1

1

1

1

1

=

0 jT

(λ1X1, Qj, Qk) =

λ1jT X1

jT Qj

jT Qk

=

@ kT

A

0

@

λ1kT X1

kT Qj kT Qk

A

λ1

0

0

1

=

@

0

a220

a230

A

.

0

a230

a330

Для кривых второго порядка существование ортонормированного базиса,в котором матрица квадратичной части диагональна,было установлено.Пусть ортогональная матрица перехода к этому базису матрица D:

D =	d11		d12	.
	d21		d22
Тогда матрица перехода к ортонормированному базису из условия теоремы будет
иметь вид	0	1	0	0	1 .
C = (X1, j, k)		0	d11 d12
	@	0	d21	d22	A

Матрица C ортогональна как произведение двух ортогональных матриц.

102

Следствие54.1. Коэффициенты λj (j = 1, 2, 3) равны собственным числам матрицы Q,а в качестве базисных векторов можно выбрать собственные векторы матрицы Q.Необходимо их ортогонализовать(если имеется два собственных вектора,принадлежащих одному и тому же собственному числу)и нормировать.

Замечание. Если у матрицы Q имеется собственное число λ1 кратности 3,то уравнение поверхности сразу имеет требуемый вид.

Действительно,для нахождения собственных векторов имеем систему линейных

уравнений	8	(a11 − λ1)x1 + a12x2 + a13x3 = 0,
	<

: a12x1 + (a22 − λ1)x2 + a23x3 = 0, a13x1 + a23x2 + (a33 − λ1)x3 = 0

Имеется три линейно независимых собственных вектора,соответствующих собственному числу λ1 (это будет доказано в курсе алгебры).Подставим координаты каждого из этих векторов в первое уравнение системы.Получим систему из трех линейных уравнений относительно a11, a12, a13 ,определитель которой не равен нулю.Следовательно,система имеет единственное решение a11−λ1 = 0, a12 = 0, a13 = 0.Аналогично рассматриваем второе и третье уравнения.

Если имеется два собственных вектора X1, X2 ,принадлежащих одному собственному числу,то в качестве двух ортогональных собственных векторов можно взять

		(X2		, X1)
векторы X1 и X20	= X2 −				X1 .Действительно,легко проверяется,что векторы
		(X1		, X1)
X1 и X20 ортогональны( (X1, X20 ) = 0).Кроме того,вектор									X20 является собственным
вектором матрицы Q,принадлежащим собственному числу λ1 :
QX20			(X2, X1)				(X2, X1)		λ1X1 = λ1X20 .
	= QX2 −					QX1 = λ1X2 −
			(X1, X1)				(X1, X1)

Лемма54.3. Для любого многочлена второй степени в пространстве существует прямоугольная система координат,в которой он принимает один из следующих пяти видов:

(1)F = λ1x2 + λ2y2 + λ3z2 + , (λ1λ2λ3 6= 0);

(2)F = λ1x2 + λ2y2 + 2b3z, (λ1λ2b3 6= 0);

(3)F = λ1x2 + λ2y2 + , (λ1λ2 6= 0);

(4)F = λ1x2 + 2c2y, (λ1c2 6= 0);

(5)F = λ1x2 + , (λ1 6= 0).

Доказательство. В силу предыдущей теоремы,можем найти такую прямоугольную систему,в которой квадратичная часть диагональна,то есть

F = λ1x2 + λ2y2 + λ3z2 + 2b1x + 2b2y + 2b3z + b0 = 0.

Рассмотрим все возможные случаи.

(1)При λ1λ2λ3

6= 0 имеем

b1

2

b2

2

b3

2

b12

b22

b32

F = λ1 x +

+ λ2 y +

+ λ3 z +

+ b0 −

−

−

=

λ1

λ2

λ3

λ1

λ2

λ3

= λ1(x0)2 + λ2(y0)2 + λ3(z0)2 + .

103

(2)При

λ3 = 0 и λ1λ2b3 6= 0 имеем

b1

2

b2

2

b12

b22

F = λ1 x +

+ λ2

y +

+ 2b3z + b0 −

−

=

λ1

λ2

λ1

λ2

= λ1(x0)2 + λ2(y0)2 + 2b3z + = λ1(x0)2 + λ2(y0)2 + 2b3 z +

=

2b3

= λ1(x0)2 + λ2(y0)2 + 2b3z0.

(3)При

λ3 = b3 = 0 и λ1λ2 6= 0 имеем

b1

2

b2

2

b12

b22

F = λ1 x +

+ λ2 y +

+

b0 −

−

=

λ1

λ2

λ1

λ2

= λ1(x0)2 + λ2(y0)2 + .

(4)Пусть λ3 = λ2 = 0 и хотя бы один из b2, b3

не равен нулю.Тогда имеем

b1

2

b12

F = λ1 x +

+ 2b2y + 2b3z + b0 −

= λ1(x0)2 + 2c2y0,

λ1

λ1

где

b1

x0 = x +

, c2 = qb22 + b32,

λ1

2

y

=

b22

+ b32

b2y + b3z + 2 b0

− λ1 ,

0

1

1

b1

z0 =

p

1

(

b3y + b2z).

pb22 + b32

−

Такая“нормировка”функций перехода гарантирует ортогональность соответствующей матрицы и,тем самым,ортогональность замены.

Если же b2 = b3 = 0,то мы сразу имеем выражение конечного вида.

(5)Пусть λ3 = λ2 = b2 = b3 = 0 и λ1 6= 0.Тогда имеем

b1

2

b12

F = λ1 x +

+ b0 −

= λ1(x0)2 + .

λ1

λ1

Лемма доказана.

Теорема54.2.

Для любой квадрики существует прямоугольная система коорди-

нат,в которой она имеет один из следующих17видов:

x2

y2

z2

= 1, (a ≥ b ≥ c > 0),эллипсоид;

1)

+

+

a2

b2

c2

x2

y2

z2

= −1, (a ≥ b ≥ c > 0),мнимый эллипсоид;

2)

+

+

a2

b2

c2

x2

y2

−

z2

= 1, (a ≥ b > 0),однополостный гиперболоид;

3)

+

a2

b2

c2

x2

y2

z2

4)

−

−

+

= 1, (a ≥ b > 0),двуполостный гиперболоид;

a2

b2

c2

x2

y2

−

z2

= 0,

(a ≥ b > 0),конус(второго порядка);

5)

+

a2

b2

c2

x2

y2

z2

= 0,

(a ≥ b > 0),мнимый конус(второго порядка);

6)

+

+

a2

b2

c2

7)x2 + y2 = 2z, (p ≥ q > 0),эллиптический параболоид; p q

104

8)x2 − y2 = 2z, (p ≥ q > 0),гиперболический параболоид; p q

9)x2 + y2 = 1, (a ≥ b > 0),эллиптический цилиндр; a2 b2

10)x2 + y2 = −1, (a ≥ b > 0),мнимый эллиптический цилиндр; a2 b2

11)x2 + y2 = 0, (a ≥ b > 0),две мнимые пересекающиеся плоскости; a2 b2

12)x2 − y2 = 1, (a ≥ b > 0),гиперболический цилиндр; a2 b2

13)x2 − y2 = 0, (a ≥ b > 0),две пересекающиеся плоскости; a2 b2

14)y2 = 2px, (p > 0),параболический цилиндр;

15)y2 = a2 , (a > 0),две параллельные плоскости;

16)y2 = −a2 , (a > 0),две мнимые параллельные плоскости;

17)y2 = 0,две совпадающие плоскости.

Доказательство. Сначала применяем лемму,а потом для каждого из типов(1)–(5) рассматриваем все случаи.Например,возьмем(1).Возможны случаи:

Если все λi одного знака,а противоположного,то делением на − и переменой осей уравнение приводится к виду1) (эллипсоид).

Если все λi и одного знака,то делением на и переменой осей уравнение приводится к виду2) (мнимый эллипсоид).

Если все λi одного знака,а = 0,то переменой осей уравнение приводится к виду6) (мнимый конус).

Если λi разных знаков,а = 0,то переменой осей уравнение приводится к виду

5) (конус).

Если λi разных знаков,причем у одного тот же знак,что и у ,то переменой осей и делением на − уравнение приводится к виду3) (однополостный гиперболоид).

Если λi разных знаков,причем у двух тот же знак,что и у ,то переменой осей и делением на − уравнение приводится к виду4) (двуполостный гиперболоид).

Таким образом,случай(1)дает1)–6).Аналогично с другими:

(1)	1),2),3),4),5),6)
(2)	7),8)
(3)	9),10),11),12),13)
(4)	14)
(5)	15),16),17)

Напомним,что рангом матрицы называется наибольшее количество линейно независимых столбцов этой матрицы.Ранг матрицы по столбцам равен рангу матрицы по строкам.Ранг матрицы равен порядку наибольшего ненулевого минора этой матрицы.

Лемма54.4. Ранг матрицы не изменяется при домножении ее на невырожденную матрицу.

Доказательство. Домножим данную матрицу A на матрицу C (det C 6= 0) справа и рассмотрим матрицу AC .Очевидно,что rank (AC) не может быть больше rank A, так как столбцы этой матрицы являются линейными комбинациями столбцов матрицы A.Предположим,что rank (AC) < rank A.Теперь снова домножим матрицу AC справа на матрицу C−1 .В результате этого домножения ранг полученной матрицы может снова уменьшиться или остаться неизменным.Тем самым,мы получим,что rank (A) < rank (A),что невозможно.Полученное противоречие доказывает лемму.

105

Аналогично доказывается данное утверждение для умножения матрицы A на матрицу C слева.

Следствие54.2. При переходе к новой системе координат ранги матриц A и Q не изменяются.

Теорема54.3. Каноническое уравнение,в отличие от канонической системы координат,определено однозначно(для видов5, 6, 11, 13 с точностью до множителя).

Доказательство. Так же,как и в случае кривых,доказывается,что коэффициенты (в частности,определитель δ и след S )и корни характеристического многочлена матрицы Q являются ортогональными инвариантами,и что инвариантом является определитель матрицы A.По следствию54.2инвариантны ранги r и R матриц Q и A соответственно.

Тогда поверхность однозначно относится к одному из типов(1)–(5),так как

(1)r = 3, R = 3 или R = 4

(2)r = 2, R = 4

(3)r = 2, R = 2 или R = 3

(4)r = 1, R = 3

(5)r = 1, R = 1 или R = 2

	Внутри типа(1)	λi (i = 1, 2, 3) инварианты,а = /δ .Внутри типа(2) λ1 ,
λ2 инварианты,а		b32 = −		.
			λ1λ2

Остальные поверхности,являясь цилиндрическими,имеют канонические уравнения,не содержащие z.Допустим,имеется замена прямоугольных координат,переводящая одно из таких уравнений в другое.Тогда x и y не зависят от z0 (и поэтому доказательство сводится к рассмотренному двумерному случаю).Докажем это,на-

пример,для уравнения вида λx2 + µy2 + = 0.Пусть x = c11x0 + c21y0 + c31z0 + c1 и y = c12x0 + c22y0 + c32z0 + c2 ,а результирующее выражение не зависит от z0 .Тогда

λc11c31	= −µc12c32,
λc21c31	= −µc22c32,
λc31c31	= −µc32c32,
λc1c31	= −µc2c32,

в частности,если хотя бы одно из c31 и c32 отлично от нуля,то две первые строки матрицы перехода линейно зависимы,и получаем противоречие.

Уравнения распадающихся поверхностей(11, 13, 15, 16, 17)определяются однозначно также из геометрических соображений.

106

ЛЕКЦИЯ17.ОСНОВНЫЕ ВИДЫ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА

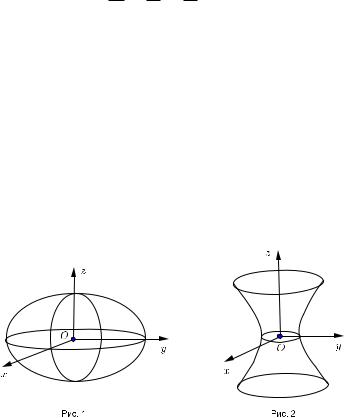
§55.Эллипсоид

Уравнение эллипсоида

x2 y2 z2

a2 + b2 + c2 = 1.

Эллипсоид изображен на рис. 1.

Поскольку |x| a, |y| b, |z| c,то эллипсоид ограничен.

Теорема55.1. Плоское сечение поверхности второго порядка есть кривая порядка не выше двух.

Доказательство. Выберем систему координат,в которой секущая плоскость имеет уравнение z = 0.Тогда уравнение сечения G(x, y) = F (x, y, 0) = 0 это уравнение кривой второго порядка.

Следствие55.1. Непустое плоское сечение эллипсоида эллипс или точка.

Доказательство. Это единственные непустые ограниченные кривые0, 1,или2-го порядка.

	§56.Однополостный гиперболоид
	Уравнение однополостного гиперболоида
		x2		y2	z2
			+		−		= 1.
		a2		b2		c2
	Однополостный гиперболоид изображен на рис. 2.
	В сечении плоскостью z = 0 получается эллипс							x2	+	y2	= 1,называемый горло-
								a2		b2
	вым.

Определение. Прямолинейной образующей поверхности называется прямая,целиком в ней содержащуюся.Как правило,это понятие не применяется к распадающимся поверхностям.

Однополостный гиперболоид обладает следующим замечательным свойством.

Теорема56.1. Однополостный гиперболоид имеет два семейства прямолинейных образующих.Через каждую точку проходит ровно одна прямая каждого семейства, и эти две прямые пересекаются ровно по этой точке.Две различные прямые из одного семейства скрещиваются,а из разных пересекаются или параллельны.

107

108

Доказательство. Перепишем уравнение однополостного гиперболоида в виде

x2

z2

y2

−

= 1 −

,

a2

c2

b2

или

a

− c

a

+ c

=

1 − b

1 + b

.

x

z

x

z

y

y

Рассмотрим пару вещественных чисел λ, µ,не равных нулю одновременно,и для каждой такой пары запишем систему уравнений

λ xa − zc = µ 1 − yb , µ xa + zc = λ 1 + yb .

Для каждой пары чисел λ, µ эти уравнения определяют пару плоскостей,которые

не параллельны.Действительно,		−b	"
"	a
"	λ	µ	"		λ2		µ2
	a	b
"	µ	λ	"	= −	ab		−	ab	< 0.
"			"
Следовательно,эти плоскости"	пересекаются"					по прямой.Каждая точка этой прямой

лежит на гиперболоиде.В самом деле,ее координаты удовлетворяют каждому из уравнений плоскостей,а значит,удовлетворяют и уравнению,полученному их перемножением,т.е.уравнению гиперболоида.Случай,когда одно из чисел λ, µ нулевое, не является исключением.Так,при λ = 0, µ 6= 0 получаем,что

1 − yb = 0, xa + zc = 0,

и уравнение гиперболоида выполняется.

Таким образом,мы получили семейство прямолинейных образующих однополостного гиперболоида,будем называть его семействомI .

Докажем,что через каждую точку гиперболоида M(x0, y0, z0) проходит ровно одна прямая данного семейства.

Для определения значения λ : µ для искомой прямой имеем систему уравнений

λ : µ = 1 − yb0 : xa0 − zc0 , λ : µ = xa0 + zc0 : 1 + yb0 ,

причем выполнено равенство

1 − yb0 : xa0 − zc0 = xa0 + zc0 : 1 + yb0 ,

получающееся из условия принадлежности точки M гиперболоиду.Поскольку хотя бы одно из чисел 1+y0, 1−y0 отлично от нуля,отношение λ : µ находится однозначно. Это отношение и задает прямую семействаI,проходящую через точку M(x0, y0, z0).

Никакие две прямые семействаIне пересекаются.Действительно,если бы они пересекались,то тогда через одну точку проходили бы две прямые семейства,что невозможно.

Никакие две прямые семействаIне параллельны.Для доказательства этого рассмотрим направляющие векторы прямых,по которым пересекаются плоскости.Эти векторы равны

"

µ

−

λ

" ,

"

−

λ

λ

"

, "

λ

µ

"! =

λ2 + µ2

2λµ

λ2 + µ2

b

c

c

a

a

b

, −

, −

λ

µ

µ µ

µ

λ

bc

ac

ab

"

−

b

c

"

"

c

a

"

"

a

−

b

"

"

"

"

"

"

"

"

"

"

"

"

"

"

"

"

"

"

"

и

"

µ0

λ0

"

"

λ0

λ0

"

"

λ0

µ0

"

λ02

+ µ02

2λ0µ0 λ02 + µ02

"

−

b

c

"

"

c

a

"

"

a

−

b

"

"

λ0

−µ0

"

,

" −

µ0

µ0

"

,

"

µ0

λ0

"!

=

bc

, −

ac

, −

ab

.

"

"

"

"

"

"

"

b

c

"

"

c

a

"

"

a

b

"

Эти векторы коллинеарны тогда и только тогда,когда пропорциональны их координаты,т.е.

λ2	+ µ2		λµ
		=		.
λ02 + µ02			λ0µ0

Преобразуем это выражение:

λ0µ0µ2 + λ0µ0λ2 = λµµ02 + λµλ02, µµ0(λ0µ − µλ0) = λλ0(µλ0 − µ0λ),

(µµ0 − λλ0)(λ0µ − λµ0) = 0.

Если λµ0 = λ0µ,то пары плоскостей,а следовательно,и прямые совпадают. Следовательно, λλ0 = µµ0 .В этом случае уравнения прямых имеют вид

λ

a

− c

= µ

1 − b

, µ

a

+ c

= λ

1 + b

x

z

y

x

z

y

и

a

− c

= λ 1 − b

, λ a

+ c

= µ 1 + b .

µ

x

z

y

x

z

y

Сложим первое и последнее уравнения и второе и третье,полученные уравнения

разделим на2:

λxa = µ, µxa = λ.

Первое из этих уравнений умножим на x/a,получим

	x2	x		= λ, rmили	λ	x2	− 1 = 1.
λ		= µ
	a2		a			a2
Если λ = 0,то и µ = 0,что невозможно.Если же							x = ±a (сечение плоскостью,

параллельной плоскости Oyz),то λ = ±µ,и опять-таки имеем совпадающие прямые. Тем самым,никакие две прямые из семействаIне параллельны.

Аналогично для любой пары чисел λ, µ рассмотрим систему уравнений

λ xa + zc = µ 1 − yb , µ xa − zc = λ 1 + yb ,

также определяющую прямую,лежащую на гиперболоиде.Данное семейство прямых будем называть семействоII .Аналогично тому,как это было сделано для прямых семействаI,можно убедиться,что через каждую точку гиперболоида проходит ровно одна прямая семействаIIи никакие две прямые этого семейства не параллельны.

Семейства не пересекаются,так как отображение (x, y, z) ! (−x, −y, −z) переводит прямые одного семейства в прямые другого,параллельные своим прообразам. Действительно,если бы прямая принадлежала обоим семействам,то ее образ также,и тем самым,мы имели бы две параллельные прямые из одного семейства.

Теперь рассмотрим две прямые l1 и l2 из разных семейств.Пусть плоскость, проходящая через l1 и некоторую точку P 2 l2 , P 62l1 .Поэтому соответствующее плоское сечение гиперболоида,являясь по теореме55.1кривой порядка не выше2,

109

должно быть парой парллельных или пересекающихся прямых.Одна из них l1 , а другая некоторая прямолинейная образующая l,проходящая через P .Она не совпадает и не скрещивается с l1 ,поэтому,по доказанному,не может принадлежать первому семейству,значит,принадлежит второму и в силу единственности прямой второго семейства,проходящей через P ,совпадает с l2 .

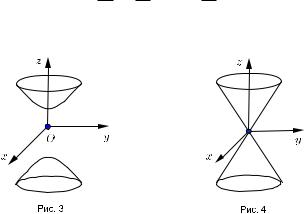
§57.Двуполостный гиперболоид

Уравнение двуполостного гиперболоида

	x2	y2		z2
−		−		+		= 1.
	a2		b2		c2

Двуполостный гиперболоид изображен на рис. 3.

Плоскость z = 0 не пересекает гиперболоид и разделяет его на две части,назы-

ваемые полостями.

Теорема57.1. Двуполостный гиперболоид не имеет прямолинейных образующих.

Доказательство. Прямолинейная образующая не может пересекать плоскость z = 0,значит,она лежит в плоскости z = z0 .Но соответствующее плоское сечение

−x2 − y2 = 1 − z02

a2 b2 c2

ограничено(эллипс,точка или пустое множество)и не может содержать прямую.

§58.Конус второго порядка
Уравнение конуса второго порядка
	x2		y2	z2
		+		−		= 0.
	a2		b2		c2
Конус второго порядка изображен на рис. 4.
Заметим,что уравнение однородно(второго порядка):							F (λx,λy,λz ) =
λ2F (x, y, z),и таким образом,любая прямая,содержащая точку							O и некоторую дру-
гую точку конуса,является прямолинейной образующей.

Определение. Пусть F произвольная кривая,лежащая в плоскости ,а точка O не принадлежит . Конической поверхностью над F с центром в O называется объединение всех прямых вида OX , X 2 F (рис. 5).Прямые OX называеются образующими,а кривая F направляющей конической поверхности.

Теорема58.1. Коническая поверхность над эллипсом является конусом второго порядка.

110