geometry24

то есть векторы (A1, B1, C1) и (A2, B2, C2) коллинеарны,что противоречит условию. Для того чтобы доказать параллельность вектора ( ,β,γ ) рассматриваемым

плоскостям,нужно доказать,что

A1 + B1β + C1γ = 0

A2 + B2β + C2γ = 0.

Подставим координаты данного вектора в первое уравнение:

"

"

"

"

"

"

"

"

A2

B2

C2

"

B1 C1

"

"

C1

A1

"

"

A1

B1

"

"

A1

B1

C1

"

A1

"

B2 C2

"

+ B1

"

C2

A2

"

+ C1

"

A2

B2

"

=

"

A1

B1

C1

"

= 0.

"

"

"

"

"

"

"

"

"

"

Аналогично для второго уравнения.

"

"

Для того чтобы перейти к каноническим уравнениям прямой,остается найти

точку,через которую проходит прямая(начальную точку).В случае						"	A1	B1	"	6=
							A2	B2
0 можно положить z равным какому-либо числу z1 ,например, z1						="	0,и найти"
						"			"
соответствующие ему значения x1 и y1 из системы уравнений(28.1):						"			"
x1 =	B1D2 − B2D1	, y1	=	A2D1 − A1D2	.
	A1B2 − A2B1			A1B2 − A2B1

Определение. Множество прямых пространства,проходящих через данную точку, называется собственной связкой прямых (сама точка называется центром связки). Множество прямых пространства,параллельных данной прямой,называется несоб-

ственной связкой прямых.

Те прямые связки,которые лежат в одной и той же плоскости,образуют пучок прямых.

Очевидно,что уравнения любой прямой,принадлежащей собственной связке с центром в точке (x0, y0, z0),могут быть записаны в виде

x − x0	=	y − y0	=	z − z0	,
		β		γ

где ( ,β,γ ) координаты направляющего вектора прямой.Придавая им различные значения(не равные нулю одновременно),можно придать прямой любое направление,т.е.получить любую прямую связки.

Уравнения любой прямой,принадлежащей несобственной связке прямых,параллельных прямой с направляющим вектором ( ,β,γ ) также имеют вид

x − x0	=	y − y0		=	z − z0	,
		β			γ
только произвольные значения	здесь		нужно придавать координатам точки

(x0, y0, z0),через которую проходит прямая несобственной связки.

§29.Некоторые формулы в прямоугольной системе координат

1.Угол между прямыми

Определение. Углом между прямыми называется наименьший из углов между прямыми,параллельными данным,проходящими через одну точку.

51

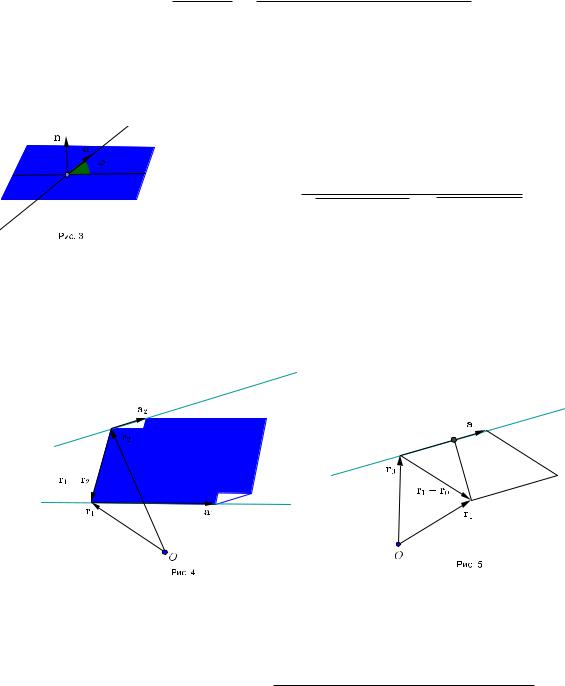
Пусть прямые имеют параметрические уравнения r = r1 + a1t и r = r2 + a2t,

где координаты векторов a1 = ( 1, β1, γ1), a2 = ( 2						, β2, γ2).Тогда угол между ними
находится по формуле
cos ' =	|(a1, a2)|	=		| 1 2 + β	1	β2	+ γ1γ2|		.
	|a1| · |a2|		p 12 + β12 + γ12 · p 22 + β22					+ γ22

2.Угол между прямой и плоскостью

Определение. Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость.

Пусть прямая имеет параметрическое уравнение r = r0 + at,а плоскость задана
общим уравнением Ax + By + Cz + D = 0,где		a = ( ,β,γ ).
Тогда угол между ними находится по формуле
sin ' =	|A + Bβ + Cγ|	.
	pA2 + B2 + C2 · p 2 + β2 + γ2

Это косинус угла между прямой,перпендикулярной плоскости,и направляющим вектором прямой(рис. 3).

3.Расстояние между скрещивающимися прямыми с параметрическими

уравнениями r = r1 + a1t и r = r2 + a2t,где r1 = (x1, y1, z1), r2 = (x2, y2, z2), a1 = ( 1, β1, γ1), a2 = ( 2, β2, γ2).Построим параллелепипед со сторонами r1 −r2 , a1 и a2 .Тогда искомое расстояние высота этого параллелепипеда.

"det 0

1

β1

γ1

1"

"

x1

− x2

y1 − y2

z1 − z2

A"

% = = |

− | =

@

2

2

2 .

V

(a1, a2, r1

r2)

"

2

β2

γ2

"

"

"

s

"

β2 γ2

"

+ "

γ2

2

"

+ " 2

β2

"

S

[a1, a2]

"

"

"

"

"

"

"

|

|

"

β1 γ1

γ1

1

1

β1"

"

"

"

"

"

"

"

4.Расстояние от точки с радиус"

-вектором" "

r1

до прямой" "

с параметриче"

-

ским уравнением r = r0 + at.Построим параллелограмм со сторонами r1 − r0 и a.

52

Тогда искомое расстояние высота этого параллелограмма(рис. 5).

% =

S

=

|[r1 − r0, a]|

=

|a|

|a|

s

"

β

γ

"

2

"

γ

"

2

"

β

"

2

"

y1 − y0

z1 − z0

"

+

"

z1 − z0

x1 − x0

"

+

"

x1 − x0

y1 − y0

"

=

.

"

"

"

"

"

"

2 + β2 + γ2

"

"

"

p

"

"

"

53

ЛЕКЦИЯ9.ЭЛЛИПС,ГИПЕРБОЛА,ПАРАБОЛА

§30.Геометрические определения эллипса,гиперболы и параболы

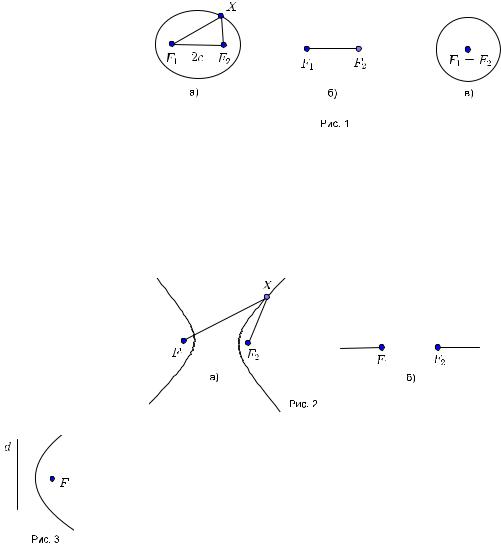
Определение. Эллипсом называется геометрическое место точек( г.м.т. ) X на плоскости,сумма расстояний от которых до двух данных точек F1 и F2 равна заданному числу:

|XF1| + |XF2| = 2a.

Точки F1 и F2 называются фокусами эллипса.

Будем считать,что a > c ≥ 0,где 2c = |F1F2| (рис. 1а).В случае a = c получаем отрезок(рис. 1б),а в случае c = 0 окружность(рис. 1в).

Определение. Гиперболой называется г.м.т. X на плоскости,модуль разности расстояний от которых до двух данных точек F1 и F2 равен заданному числу:

||XF1| − |XF2|| = 2a.

Точки F1 и F2 называются фокусами гиперболы.

Будем считать,что c > a > 0, где 2c = |F1F2| (рис. 2а).В случае a = c получаем два противоположно направленных луча

(рис. 2б),выходящих из фокусов.

Определение. Параболой называется г.м.т. X плоскости,равноудаленных от данной точки F ,называемой фокусом,и данной прямой d,называемой директрисой:

|XF | = %(X, d).

Предполагается,что F 62d.

§31.Эллипс,гипербола и парабола как конические сечения

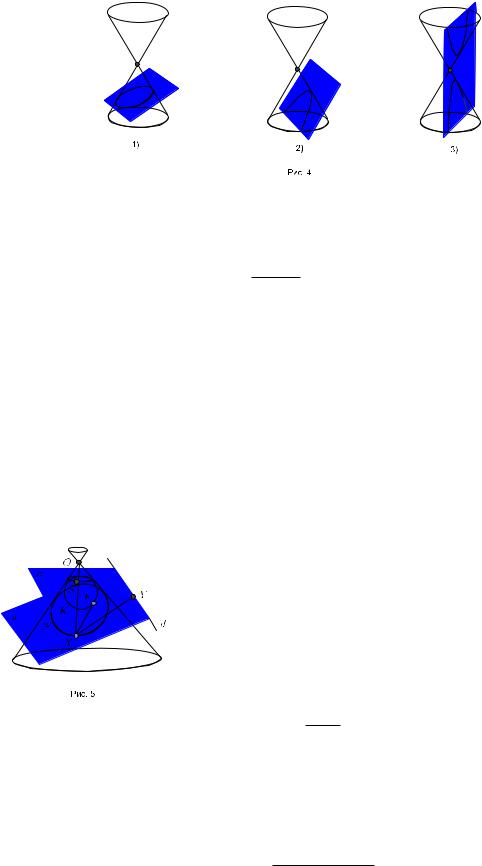
Рассмотрим сечение прямого кругового бесконечного в обе стороны конуса плоскостью.Будем считать,что данная плоскость не проходит через вершину конуса.

Плоскость может пересекать1)одну половину конуса по замкнутой ограниченной кривой, 2)пересекать одну половину конуса по неограниченной кривой или3) пересекать обе половины конуса.

54

Теорема31.1. Каждое коническое сечение,отличное от окружности,является множеством точек X ,отношение расстояний от которых до некоторой точки F к расстоянию до некоторой прямой d (F 62d)равно постоянной величине:

|XF |	= e.
%(X, d)

Доказательство. Для доказательства будем использовать шары Данделена шары,вписанные в конус и касающиеся данной плоскости.

Пусть угол между осью конуса и его образующей, β угол между осью конуса и плоскостью сечения( β < /2).

Впишем в конус шар K ,касающийся плоскости сечения в точке F и касающийся конуса по окружности c.Пусть плоскость пересекается с плоскостью σ , в которой лежит окружность c,по прямой d.Обозначим через F кривую,по которой плоскость сечения пересекает конус.

Рассмотрим произвольную точку X кривой F .Пусть Y основание перпендикуляра,опущенного из X на d, а S точка пересечения образующей конуса XO с окружностью c (на рис. 5изображен случай1),в случаях2)и3)рисунки будут

аналогичные). |XF | = |XS| как касательные к шару,

проведенные из одной точки.Отрезок

XS образует с

осью конуса угол ,а отрезок

XY угол β .Проек-

ции отрезков XS и XY на ось конуса равны,откуда

получаем,что

|XF | cos = |XY | cos β,

откуда сразу следует,что

|XF |

=

cos β

= e = const.

|XY |

cos

|XF |

= cos β

X

Очевидно,что если точка

не принадлежит конусу,то

6

.

|XY |

cos

Меняя углы и β ,мы можем придать отношению

cos β

любое значение,боль-

cos

шее нуля.

%(F, d) = r(sin + sin β), cos β

где r радиус шара K ,что сразу же следует из рассмотрения осевого сечения конуса(рис. 6).

55

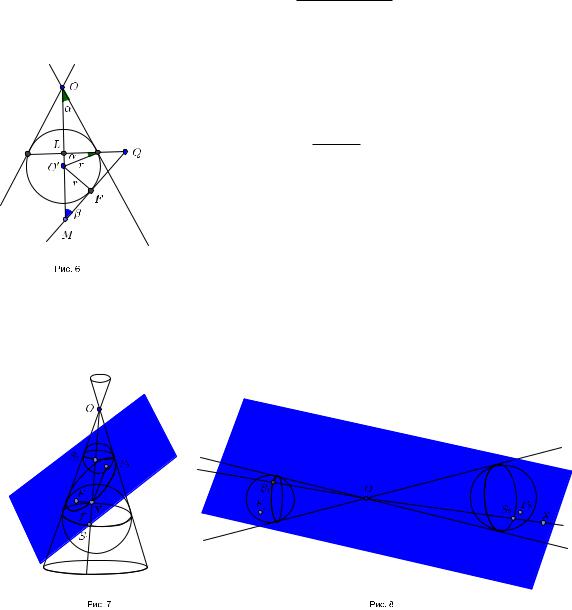
Действительно,

|

O0L

|

= r sin ,

|

O0M

|

=

r

,

|

MQ

|

=

|LO0| + |O0M|

,

|

F Q

|

=

|

MQ

| − |

MF

.

sin β

cos β

|

Таким образом,расстояние от точки

F до прямой d пропорционально радиусу

шара K .Тем самым,выбирая подходящим образом ради-

ус шара(или расстояние от вершины конуса до плоскости

сечения),можно придать

%(F, d) любое значение.

Следовательно,любое множество точек X ,удовлетво-

ряющих условию

|XF |

= e,где

F фиксированная

точка,а

%(X, d)

d фиксированная прямая,можно описать как

коническое сечение.

Определение. Прямая d называется директрисой кони-

ческого сечения,величина

e эксцентриситетом.Дока-

занная теорема называется директориальным свойством

конических сечений.

Теорема31.2. В случае 1)

получается эллипс,в случае

2)

парабола,в случае 3)

гипербола.

Доказательство.

Вершину конуса обозначим через O.

Первый случай. Пусть F интересующее нас сечение конуса плоскостью . Обозначим через F1 и F2 точки касания шаров Данделена и плоскости ,а через c1 и c2 окружности касания шаров с конусом.Пусть X произвольная точка на сечении F .Пусть S1 и S2 точки пересечения OX с c1 и c2 соответственно

(рис. 7).

Тогда,так как равны касательные,проведенные к шару из одной точки:

|XF1| = |XS1|, |XF2| = |XS2|,

|XF1| + |XF2| = |XS1| + |XS2| = |S1S2| = const.

Второй случай сразу следует из предыдущей теоремы. Третий случай. Сохраним прежние обозначения(рис. 8).

Тогда,так как равны касательные,проведенные к шару из одной точки:

|XF1| = |XS1|, |XF2| = |XS2|,

56

||XF1| − |XF2|| = ||XS1| − |XS2|| = |S1S2| = const.

Определение. В соответствии с доказанными теоремами эллипс,гипербола и парабола называются также кониками.

§32.Аналитическое определение коник

Определение. Кривая второго порядка,задаваемая в некоторой прямоугольной системе координат уравнением

	x2	y2						(a ≥ b);
		+			= 1,
	a2		b2
называется эллипсом,
уравнением			x2				y2
						−		= 1;
				a2			b2
гиперболой,
уравнением
	y2 = 2px,							(p > 0).

параболой.

Уравнения(32.1), (32.2)и(32.3)называются также эллипса,гиперболы и параболы соответственно.

(32.1)

(32.2)

(32.3)

каноническими уравнениями

Теорема32.1. Аналитические и геометрические определения эллипса,гиперболы и параболы эквивалентны.

Доказательство.Эллипс. Пусть начало прямоугольной системы координат O совпадает с серединой отрезка F1F2 ,ось абсцисс совпадает с прямой F1F2 и сонаправлена вектору OF2 .Направление оси ординат выберем так,чтобы пара векторов i, j была правой.Пусть точка X(x, y) произвольная точка эллипса(рис. 9).

Тогда геометрическое определение {X||XF1| + |XF2| = 2a} перепишется в виде

p

p

r1 + r2 = 2a, r1 = (x + c)2

+ y2, r2

=

(x − c)2

+ y2

,

= 4p

p

(x + c)2 + y2 = 2a

−

(x

−

c)2

+ y2

,

(x + c)2 + y2

a2 + (x

c)2 + y2

4a (x c)2 + y2,

−

a2 cx−= ap

−

(x

c)2

+ y2

,

a4

−

,

−

2a2cx + c2x2 = a2x−2 + a2c2 p2a2cx + a2y2

−

a4 − a2c2 = (a2 − c2)x2 + a2y2,

x2

y2

b2 = a2 − c2.

(32.4)

+

= 1,

a2

b2

57

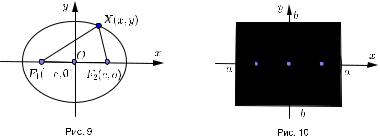
Непосредственно из уравнения видно,что эллипс заключен в прямоугольник со сторонами 2a и 2b,причем на границе его лежат лишь точки пересечения с осями

(рис. 10).

Этот прямоугольник называется основным прямоугольником эллипса. Обратно,пусть точка (x, y) удовлетворяет уравнению(32.4),то есть

y2 = b2 −

b2

x2.

a2

Тогда

b2

= (x + c)2 + y2 = rx2

r1

+ 2cx + c2 + b2

−

x2 =

a2

r

r

a2

2

a2

a

2 p

c

2

=

− b

x2 + 2cx + c2 + b2 =

x2 + 2cx + c2 + b2 =

"

c

"

c

c

= "ax + a" = a + ax,

|

|

"

"

Аналогично,

c

где выражение под знаком модуля" положительно"

,так как

x

a,

a x

c.

r2 = a − ax.

Таким образом,для любой точки,удовлетворяющей уравнению32.4,выполняется r1 + r2 = 2a,то есть она удовлетворяет геометрическому определению эллипса.

Определение. Отношение

		=	p
e =	c			a2 − b2
	a
				a

называется эксцентриситетом эллипса.Прямые,имеющие уравнения x = ±a/e называются директрисами эллипса.

Проверим,что для эллипса выполняется директориальное свойство. Действительно,для его левого" фокуса" в обозначениях предыдущей теоремы

|F1X| = r1 = a + ex, а %(X, d1) = "x + ae " = x + ae ,так что

|F1X| = e. %(X, d)

Гипербола. Пусть начало прямоугольной системы координат O совпадает с серединой отрезка F1F2 ,ось абсцисс совпадает с прямой F1F2 и сонаправлена вектору F1F2 .Направление оси ординат выберем так,чтобы пара векторов i, j была правой. Пусть точка X(x, y) произвольная точка эллипса(рис. 11).

Аналогично эллипсу,упрощая соотношение |r1 −r2| = 2a,приходим к уравнению

x2 − y2 = 1, b2 = c2 − a2. a2 b2

Обратные вычисления проводим так же,как и для эллипса,и получаем

r1 = |a + ex|, r2 = |a − ex|,

причем для правой ветви гиперболы(при x > 0)

r1 = a + ex, r2 = −a + ex,

58

а для левой ветви гиперболы(то есть при x < 0)

r1 = −a − ex, r2 = a − ex.

В любом случае |r1 − r2| = 2a,что и требовалось доказать.

Основной прямоугольник со сторонами 2a и 2b для гиперболы изображен на рис. 12.

Его диагонали имеют уравнения

y = ±ab x

и являются асимптотами гиперболы.Докажем это,например,для y = b x.Имеем

(см.рис.)

a

b

x2

b

a2

lim

lim

= 0.

ax − bra2 − 1!

x!1

= a x!1

x + px2 − a2

Для гиперболы положим эксцентриситет равным

c

p

a2 + b2

e =

=

,

a

a

а уравнения директрис останутся теми же,что и для эллипса: x = ±a/e. Таким образом,для эллипса e < 1,а для гиперболы e > 1.

Проверка директориального свойства осуществляется так же,как и для эллипса. Парабола. Для параболы положим эксцентриситет равным единице: e = 1.

Число p называется фокальным параметром.

Проведем ось абсцисс прямоугольной системы координат через фокус перпендикулярно директрисе параболы.Положим p равным расстоянию между директрисой

и фокусом.Начало координат выберем на расстоянии p/2

от фокуса и на таком

же расстоянии от директрисы.Направление оси ординат

выберем так,чтобы пара векторов

i, j была правой.

Тогда соотношение из геометрического определения пара-

болы примет вид

p2

p2

r x −

p

2

p

2

+ y2 = x +

2

,

x2 − px +

+ y2 = x2 + px +

,

4

4

y2 = 2px.

59

Обратно,для кривой,определяемой уравнением y2 = 2px обозначим через d

прямую y = −p/2,а через F

точку (p/2, 0).Заметим,что для точек этой кривой

всегда x ≥ 0,так что для произвольной ее точки

X(x, y) имеем %(X, d) = p/2 + x, а

p 2

p

2

"

p

"

p

%(X, F ) = r x −

+ y2 = r x −

+ 2px =

"x +

"

= x +

,

2

2

2

2

"

"

и геометрическое определение параболы выполняется.

60