geometry24

Доказательство.

2)	3)	(i, b) + a2	(j, b) + a3	1)
(a, b) = (a1i + a2j + a3k, b) = (a1i, b) + (a2j, b) + (a3k, b) = a1				(k, b) =
		2),3)
= a1(b1i + b2j + b3k, i) + a2(b1i + b2j + b3k, j) + a3(b1i + b2j + b3k, k) =
2),3)	(i, k) + a2b1(j, i) + a2b2(j, j) + a2b3(j, k)+
= a1b1(i, j) + a1b2(i, j) + a1b3
= a3b1(k, i) + a3b2(k, j) + a3b3(k, k) = a1b1 + a2b2 + a3b3.

Следствие1. В прямоугольной системе координат угол между векторами определяется формулой

^	(a, b)				a1b1 + a2b2 + a3b3
cos(a, b) =			=					.
	|a| · |b|			p		· p
					a12 + a22 + a32		b12 + b22 + b32

Следствие2. В прямоугольной системе координат расстояние между точками M1(x1, y1, z1) и M2(x2, y2, z2),находится по формуле

p

%(M1, M2) = (x1 − x2)2 + (y1 − y2)2 + (z1 − z2)2.

Утверждение. Для направляющих косинусов справедливо соотношение cos2 + cos2 β + cos2 γ = 1.

Доказательство. Это квадрат длины орта.

21

ЛЕКЦИЯ4.ПЛОЩАДЬ,ОБЪЕМ И ОРИЕНТАЦИЯ

§11.Ориентированная площадь

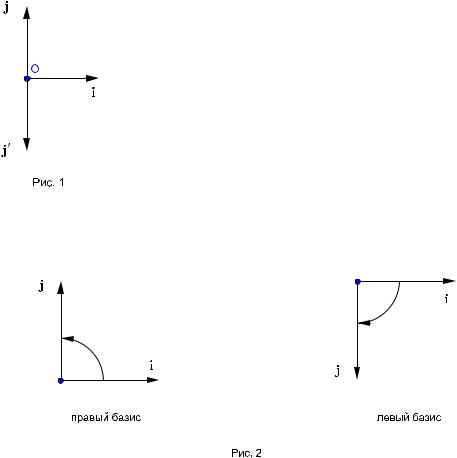
Рассмотрим на плоскости два ортонормированных базиса i, j и i0, j0 .Попробуем совместить эти базисы.Совместим векторы i и i0 .Векторы j и j0 при этом ста-

нут коллинеарными(рис. 1).Эти векторы либо совпадут,и тогда базисы будут совмещены,либо окажутся противоположно направленными,и тогда базисы совместить нельзя.

Таким образом,все ортонормированные базисы на плоскости распадаются на два класса.Два базиса из одного класса можно совместить,а два базиса из разных классов совместить нельзя.

Базис называется правым или левым в зависимости от того,в какую сторону происходит кратчайший поворот от первого базисного вектора ко второму(против часовой стрелки или по часовой

стрелке).

Определение. Положительно ориентированным,или правым,называется базис,

для которого кратчайший поворот от первого базисного вектора ко второму происходит против часовой стрелки.В противоположном случае базис называется отри-

цательно ориентированным,или левым.

Это определение распространяется на любые базисы в плоскости.

Выбор одного из двух классов базисов называется заданием ориентации плоскости.Соответственно,если выбирается класс правых базисов,то плоскость назы-

вается положительно ориентированной,если класс левых отрицательно ориентированной.

Пусть в ортонормированном базисе i, j заданы векторы a=( 1, 2) и b=(β1, β2).

Определение. Ориентированной площадью параллелограмма (a, b),построенного на векторах a, b,называется площадь этого параллелограмма,взятая со знаком “плюс”,если пара векторов a, b правая,и“минус” в противном случае.

Обозначается ориентированная площадь (a, b) через Sor(a, b).

Теорема11.1.	"			"
		1	β1
Sor(a, b) =	"			"
	"	2	β2	" .
	"			"

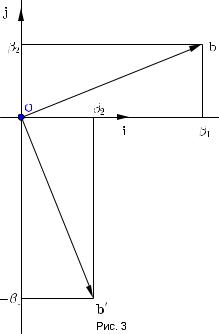
Доказательство. Рассмотрим векторы,ортогональные вектору b и равные ему по длине.Таких векторов два,и они противоположно направлены,их координаты

(−β2, β1) и (β2, −β1).

22

Поскольку площадь параллелограмма рав-
на произведению длин векторов a и b на синус
угла между ними,то она будет равна произве-
дению длин векторов a и b0 на модуль косинуса
угла между ними(первый и второй уголы отли-
чаются на /2).
Осталось проверить совпадение знаков.
Пара векторов b0, b правая(см.рис. 3).
Следовательно,если пара векторов	a, b
правая,то угол ' между векторами a и b0	бу-
дет не больше /2,и его косинус будет неотри-
цательным.А если пара векторов a, b левая,то
угол между векторами a и b0 будет не меньше
/2,и его косинус будет неположительным.
Отсюда Sor(a, b) = |a||b0| cos ' = 1β2 −
2β1 .Последнее равенство получаем,вычисляя
скалярное произведение векторов a и b0 в ор -
тонормированном базисе.
Лемма8. Ориентированная площадь обладает следующими свойствами:

1)Sor(b, a) = −Sor(a, b) (кососимметричность);

2)Sor(a + b, c) = Sor(a, c) + Sor(b, c),

3)Sor(λa, b) = λSor(a, b) (2), 3) линейность по первому аргументу);

4)Sor(a, a) = 0.

Доказательство. Все утверждения следуют из формулы для ориентированной площади и свойств определителя.

§12.Ориентированный объем

Действуем в полной аналогии с тем,как мы это делали для плоскости. Рассмотрим в пространстве два ортонормированных базиса i, j, k и i0, j0, k0 .По-

пробуем совместить эти базисы.Перенесем и повернем вектор i0 так,чтобы он совпал с вектором i.При этом плоскость векторов j0 и k0 ,перпендикулярная вектору i0 ,совместится с плоскостью векторов j и k,которая перпендикулярна i.Теперь повернем эту плоскость вокруг вектора i так,чтобы совпали векторы j и j0 .Тогда векторы k и k0 либо совпадут,и тогда базисы будут совмещены,либо окажутся противоположно направленными,и тогда базисы совместить нельзя.

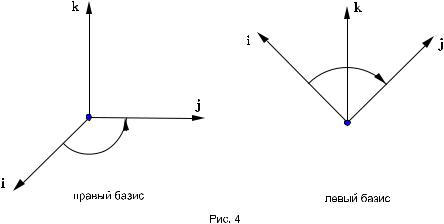
Таким образом,все ортонормированные базисы в пространстве распадаются на два класса(рис. 4).Два базиса из одного класса можно совместить,а два базиса из разных классов совместить нельзя.Базис называется правым или левым в соответ-

ствии с правилом буравчика.

Определение. Если вращать буравчик и векторы так,чтобы первый базисный вектор кратчайшим образом поворачивался ко второму,то буравчик(винт)будет завинчиваться в направлении третьего базисного вектора для правого базиса,и в направлении,противоположном направлению третьего вектора,для левого базиса.

Замечание. Под винтом и буравчиком здесь имеются в виду винт с правой резьбой,каковых абсолютное большинство в технике и что является в ней повсеместным стандартом,или буравчик также с правым винтом на острие,каково также

23

абсолютное большинство реальных инструментов).Это можно переформулировать в терминах часовой стрелки,поскольку правый винт по определению это такой винт,который завинчивается(вперед),когда мы вращаем его по часовой стрелке.

Выбор одного из двух классов базисов называется заданием ориентации пространства.Соответственно,если выбирается класс правых базисов,то пространство называется положительно ориентированным,если класс левых отрицательно ориентированным.

Определение правого и левого базиса распространяется на все базисы пространства.

Лемма9. Ориентация тройки векторов (a, b, c) противоположна ориентации тройки векторов (b, a, c).

Доказательство. Кратчайший поворот от вектора a к вектору b происходит в сторону,противоположную той,в которой осуществляется кратчайший поворот от вектора b к вектору a.

Определение. Ориентированным объемом параллелепипеда (a, b, c),построенного на векторах a, b, c называется объем этого параллелепипеда,взятый со знаком “плюс”,если тройка векторов a, b, c правая,и“минус” в противном случае.

Замечание. Мы давали определение определителя,исходя из решения системы линейных уравнений.Возможен и другой подход.Можно ввести ориентированный объем параллелепипеда,построенного на векторах a1, a2, . . . , an в пространстве Rn (считая известным ориентированный объем параллелепипеда в пространстве Rn−1 ), рассмотреть его свойства и доказать единственность.Далее матрице,составленной из координат рассматриваемых векторов,сопоставляется число,равное данному ориентированному объему.Это число и называется определителем матрицы.Такой подход можно найти,например,в книге В.В.Прасолова,В.М.Тихомирова“Геометрия”.

§13.Векторное и смешанное произведения векторов

Определение. Векторным произведением векторов a и b в ориентированном пространстве называется вектор c,обозначаемый [a, b] и определяемый следующим образом:

1)длина c равна площади параллелограмма (a, b);

2)вектор c перпендикулярен a и b;

3)тройка a, b, c правая.

По определению ориентации такой вектор c существует и однозначно определен.

24

Если векторы a и b коллинеарны,то c = 0.

Замечание. Исторически понятие векторного произведения тоже имеет физические корни.При движении двух заряженных частиц в одной плоскости возникает сила,перпендикулярная этой плоскости,модуль которой пропорционален зарядам этих частиц и синусу угла между скоростями.

Лемма10. Пусть i, j, k положительно ориентированный ортонормированный базис.Тогда

[i, j] = k, [i, k] = −j, [j, k] = i.

Доказательство. Получаем эти равенства сразу же,применяя определение векторного произведения и учитывая,что тройка векторов i, j, k правая,а длины всех этих векторов равны1.

Определение. Число (a, b, c) = ([a, b], c) называется смешанным произведением

тройки a, b, c.

Теорема13.1. (a, b, c) = Vor(a, b, c).

Доказательство. Абсолютные значения величин в левой и правой частях равенства совпадают,поскольку модуль смешанного произведения также равен объему параллелепипеда,построенного на векторах a, b, c.

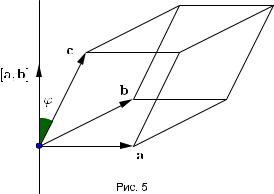
В самом деле,объем параллелепипеда равен(рис. 5)произведению площади основания [a, b] на высоту |c|| cos '|.Здесь ' угол между векторами c и [a, b]. Поэтому можно записать

V = |[a, b]||c|| cos '| = |([a, b], c)| = |(a, b, c)|.

Знак смешанного произведения совпадает со знаком cos '.Поэтому смешанное произведение положительно,когда вектор c направлен в ту же сторону от плоскости векторов a и b,что и вектор [a, b],т.е.в том случае,если тройка векторов a, b, c правая.Смешанное произведение отрицательно,когда вектор c направлен в другую сторону от плоскости векторов a и b,чем вектор [a, b],т.е. в том случае,если тройка векторов a, b, c левая.

Теорема13.2. Смешанное произведение кососимметрично по любой паре аргументов и линейно по каждому из них:

1) (a, b, c) = −(b, a, c) = (b, c, a) = −(c, b, a) = (c, a, b) = −(a, c, b);

2) (a + b, c, d) = (a, c, d) + (b, c, d),	(λa, b, c) = λ(a, b, c),
(a, b + c, d) = (a, b, d) + (a, c, d),	(a, λb, c) = λ(a, b, c),
(a, b, c + d) = (a, b, c) + (a, b, d),	(a, b, λc) = λ(a, b, c).

Доказательство. 1)По предыдущему утверждению абсолютная величина(объем параллелепипеда)не меняется.Утверждение про знаки следует из леммы9.

2)Линейность по третьему аргументу следует из линейности скалярного произведения векторов.Из этого при помощи п. 1следует линейность по остальным аргументам.

25

Теорема13.3. Векторное произведение обладает следующими свойствами:

1)[a, b] = −[b, a];

2)[λa, b] = λ[a, b];

3)[a + b, c] = [a, c] + [b, c].

Доказательство. Пп. 1) и 2) сразу вытекают из определения.Для доказательства п. 3) рассмотрим вектор d = [a + b, c] − [a, c] − [b, c].Найдем

(d, d) = ([a + b, c] − [a, c] − [b, c], d) = (a + b, c, d) − (a, c, d) − (b, c, d) = 0.

Отсюда d = 0,а это и есть п. 3.

Теорема13.4. Пусть i, j, k ортонормированный базис положительной ориента-

ции, a = ( 1, 2, 3), b = (β1, β2, β3), c = (γ1, γ2, γ3).Тогда

	"	i	j k	"		"	1	2	3	"
[a, b] =	"	1	2 3	"	, (a, b, c) =	"	β1	β2	β3	"
	"			"		"				" .
	"			"		"				"
	"	β1	β2 β3	"		"	γ1	γ2	γ3	"
	"			"		"				"

Доказательство. Воспользуемся предыдущей теоремой и леммой10:

[a, b] = [ 1i + 2j + 3k, β1i + β2j + β3k] =
1β1	[i, i] + 1β2 [i, j] + 1β3				[i, k] + 2β1		[j, i] + 2β2	[j, j] +
2	|{z}3	+ 3	β|{z}1 [	3	|{z}2	3	|{z}3	|{z}
	=0		=k		=−j		=−k	=0
+ β [j, k]			k, i] + β [k, j] + β [k, k] =
	|{z}		|{z}		|{z}		| {z }
	=i		=j		=−i		=0

( 2"β3 −

= """ 2

β2

3β2)i + ( 3β1 − 1β3)j + ( 1β2 − 2β1)k =

3	"	"	3 1	"	"	1	2	"
β3	"	"	β3 β1	"	"	β1	β2	"
	" i +	"		" j +	"			" k.
	"	"		"	"			"

Для доказательства второго соотношения воспользуемся определением смешанного произведения,первым соотношением и записью скалярного произведения в прямоугольных координатах

"

2

3

"

"

3

1

"

"

1

2

"

(a, b, c) = ([a, b], c) =

"

β2

β3

"

γ1

+

"

β3

β1

"

γ2

+

"

β1

β2

"

γ3

=

"

"

"

"

"

"

"

1

2

3

"

"

"

"

"

"

"

=

"

β1

β2

β3

"

"

".

"

"

"

γ1

γ2

γ3

"

"

"

§14.Двойное векторное произведение

Теорема14.1. Имеют место следующие формулы:

1)[a, [b, c]] = b(a, c) − c(a, b) (формула двойного векторного произведения или “бац”минус“цаб”;

2)[a, [b, c]] + [b, [c, a]] + [c, [a, b]] = 0 (тождество Якоби).

Доказательство. 1)выберем ортонормированный базис i, j, k положительной ориентации так,что

a = ( 1, 2, 3), b = (β1, β2, 0), c = (γ1, 0, 0),

26

то есть i сонаправлен с c, j лежит в плоскости b, c.Тогда

"

β

0

"

"

0

β1

"

"

β1

β2

"

"

02

"

"

"

"

"

[b, c] =

"

0

"

, "

0 γ1

"

,

"

γ1

0

" = (0, 0, −β2γ1).

"

"

2

"

"

3

"

" "

3

"1

"

"

1 2

"

[a, [b, c]] =

0

−

,

"

−

β2γ1

0

0 0

=

"

β2γ1 "

"

" ,

"

"

"

−

"

"

"

"

"

"

= (

2

β2"γ1", 1β2γ1, 0).

" "

"

С другой стороны,
	(a, c) = 1γ1,	b(a, c) = ( 1γ1β1, 1γ1β2, 0),
	(a, b) = 1β1 + 2β2, c(a, b) = (γ1 1β1 + γ1 2β2, 0, 0),
откуда	b(a, c) − c(a, b) = (−γ1 2β2, 1γ1β2, 0) = [a, [b, c]].
2)По п.	1:	[a, [b, c]] = b(a, c) − c(a, b)
+
		[b, [c, a]] = c(b, a) − a(b, c)
		[c, [a, b]] = a(c, b) − b(c, a)

[a, [b, c]] + [b, [c, a]] + [c, [a, b]] = 0

27

ЛЕКЦИЯ5.ЗАМЕНЫ КООРДИНАТ.СИСТЕМЫ КООРДИНАТ

§15.Замены координат

Приведем сначала некоторые сведения из алгебры,которые понадобятся в дальнейшем.

Определение. Матрицей называется специальная таблица

	a11	a12 . . .
A =	0 a21	a22 . . .
	@
	B a. . .	a	m2	. . .
	B m1

в которой m строк и n столбцов.

a1n		C
a
a2n		1		,
		A
	mn Cm			n

Обозначение: A = [aij]m n .

Для матриц одной и той же размерности определяются операции

A + B = [aij + bij], A − B = [aij − bij],

λA = [λaij], AT = [aji]n m транспонирование.

Определение. Пусть

A = [aij]m n, B = [bij]n k

(число столбцов матрицы A совпадает с числом строк матрицы B ).Тогда определено

произведение матриц A и B :

C = AB = [cij]m k,

где

cij = ai1b1j + ai2b2j + . . . + ainbnj.

Элемент cij ,стоящий в i-й строке j -м столбце матрицы C равен произведению i-й строки матрицы A на j -й столбец матрицы B .

Определение. Обратной матрицей к квадратной матрице A (размерности n n) называется матрица A−1 ,такая,что AA−1 = E ,где E единичная матрица(по главной диагонали стоят единицы,а все остальные элементы нулевые).

Выполняются следующие свойства(во всех пунктах,кроме первого,матрицы квадратные):

1)(AB)T = BT AT ;

2)det AT = det A;

3)det(AB) = det A · det B ;

4)(A−1)T = (AT )−1 (если обратная матрица существует). Теперь перейдем к рассмотрению замен координат.

Пусть в пространстве имеются два базиса:старый e1, e2, e3 и новый e01, e02, e03 .Разложим новые базисные векторы по старому базису:

8

< e01 = c11e1

:e02 = c12e1 e03 = c13e1

+ c21e2 + c31e3,

+ c22e2 + c32e3, (15.1) + c23e2 + c33e3.

28

Определение. Матрицей перехода от базиса e1, e2, e3 к базису e01, e02, e03 называется матрица

	c11	c12	c13	1
C =	0 c21	c22	c23		,
	@ c31	c32	c33	A

то есть матрица,по столбцам которой стоят координаты новых базисных векторов в старом базисе.

Замечание. Тройка векторов e01, e02, e03 является базисом тогда и только тогда, когда векторы линейно независимы,т.е.матрица C невырожденная( |C| =6 0).

Напомним,что аффинная система координат в пространстве задается репером

Oe1e2e3 ,а точка	M имеет координаты (x, y, z),если	OM = xe1 + ye2 + ze3 .
Теперь рассмотрим две системы координат:старую Oe1e2e3 и			новую
O0e10 e20 e30 .Пусть	C матрица перехода от базиса	e1, e2, e3 к базису	e10 , e20 , e30 ,

(x0, y0, z0) координаты точки O0 (нового начала координат)в старой системе координат, (x, y, z) и (x0, y0, z0) координаты точки в старой и новой системах координат соответственно.

Теорема15.1. Координаты точки в старой и новой системе координат связаны

соотношениями	x			x0			x0
		A			A			A
	@ z			@ z0			@ z0
	0 y	1	= C	0 y0	1	+	0 y0	1	,	(15.2)

Доказательство. Обозначим данную точку через M .Тогда

OM = OO0 + O0M, OO0 = x0e1 + y0e2 + z0e3,

O0M = OM − OO0 = x0e01 + y0e02 + z0e03 =

=x0(c11e1 + c21e2 + c31e3) + y0(c12e1 + c22e2 + c32e3) + z0(c13e1 + c23e2 + c33e3) =

=(x0c11 + y0c12 + z0c13)e1 + (x0c21 + y0c22 + z0c23)e2 + (x0c31 + y0c32 + z0c33)e3.

OM = (x0 +x0c11 +y0c12 +z0c13)e1 +(y0 +x0c21 +y0c22 +z0c23)e2 +(z0 +x0c31 +y0c32 +z0c33)e3.

Следствие3. Координаты вектора в старой ( ,β,γ ) и новой ( 0, β0, γ0) системах координат связаны соотношениями

0 1 0 0 1

@β A = C @ β0 A .

γ γ0

Доказательство. Эти формулы получаются из(15.2),если учесть,что координаты вектора равны разности координат его конца и начала.

Замечание. Всякое соотношение вида(15.2)с невырожденной матрицей C может быть проинтерпретировано как переход к некоторой новой системе координат.

Теорема15.2. Пусть C матрица перехода от базиса e1, e2, e3 к базису e01, e02, e03 , а D матрица перехода от e01, e02, e03 к e001, e002, e003 .Тогда CD матрица перехода от e1, e2, e3 к e001, e002, e003 .

Доказательство. Пусть ( ,β,γ ), ( 0, β0, γ0) и ( 00, β00, γ00) координаты одного и того же вектора в базисах e1, e2, e3 , e01, e02, e03 и e001, e002, e003 соответственно.Тогда выполнены равенства:

0		1		0		1		0	00	1
	β		= C		β00		= CD		β00		,
@	γ	A		@	γ0	A		@	γ00	A

29

откуда сразу следует требуемое.Так,подставив базисный вектор e001 в эти формулы, получим

@		A	@	0	A	@	1	A	u11	A
	γ			γ0			0		@ u31
0	β	1	= C 0	β0	1	= CD 0	0	1	= 0 u21	1 ,

т.е.первый столбец матрицы CD.

§16.Прямоугольные системы координат и ортогональные матрицы

Определение. Квадратная матрица C называется ортогональной,если CT = C−1 , то есть CT C = E и CCT = E .

Теорема16.1. Матрица C является ортогональной тогда и только тогда,когда она является матрицей перехода от ортонормированного базиса к ортонормированному.

Доказательство. Пусть

C= [cij]3 3

матрица перехода от ортонормированного базиса i, j, k к базису e1, e2, e3 . Тогда справедливы формулы(15.1):

e1 = c11i + c21j + c31k, e2 = c12i + c22j + c32k, e3 = c13i + c23j + c33k.

Если матрица C ортогональная,то
(ei, ej) = c1ic1j + c2ic2j + c3ic3j = δij =	1,	если i = j,
	0,	если i 6= j,

(δij символ Кронекера),поскольку умножаем i-ю строку матрицы C на j -й столбец матрицы CT ,т.е.на j -ю строку матрицы C .Таким образом,мы получили,что базис e1, e2, e3 также ортонормированный.

Обратно:пусть C матрица перехода от ортонормированного базиса i, j, k к ортонормированному базису i0, j0, k0 .Тогда,например,

(i0, i0) = c211 + c212 + c213 = 1,

а это произведение первой строки матрицы C на первый столбец матрицы CT ,

(i0, j0) = c11c21 + c12c22 + c13c23 = 0,

а это произведение первой строки матрицы C на второй столбец матрицы CT . Рассматривая все остальные скалярные произведения векторов i0, j0, k0 ,получаем

требуемое.

Замечание. Аналогичное утверждение очевидно справедливо и для плоскости. Утверждение. Ортогональные матрицы 2 2 имеют один из следующих видов

cos '	sin '	,	cos '	sin '	.
sin '	−cos '		sin '	−cos '

30