geometry24

Очевидно,что при проективном преобразовании она перейдет в кривую второго порядка и что определение корректно,то есть не зависит от умножения тройки однородных координат на ненулевой множитель.

По той же теореме из линейной алгебры,которой мы пользовались,когда говорили о поверхностях,существует такая проективная замена координат,что в новой системе уравнение примет вид

q0(x0) = λ1(x01)2 + λ2(x02)2 + λ3(x03)2 = 0.

Взависимости от знаков λi возможны пять случаев:

1λ1 и λ2 одного знака,а λ3 противоположного,заменой базиса уравнение приводится к виду

(x001)2 + (x002)2 − (x003)2 = 0.

2 все λi одного знака,уравнение приводится к виду

(x001)2 + (x002)2 + (x003)2 = 0.

3 λ3 = 0, а λ1 и λ2 разных знаков,тогда

(x001)2 − (x002)2 = 0.

4 λ3 = 0, а λ1 и λ2 одного знака,тогда

(x001)2 + (x002)2 = 0.

5 λ2 = λ3 = 0,тогда

(x001)2 = 0.

Мы доказали следующую теорему.

Теорема76.1. Существует система однородных координат,в которой данная кривая второго порядка имеет один из следующих видов:

1(x001)2 + (x002)2 − (x003)2 = 0 (овал);

2(x001)2 + (x002)2 + (x003)2 = 0 (мнимый овал);

3(x001)2 − (x002)2 = 0 (пара различных прямых);

4(x001)2 + (x002)2 = 0 (пара мнимых прямых);

5(x001)2 = 0 (пара совпавших прямых).

Теорема76.2. Существует ровно пять указанных классов кривых второго порядка относительно проективных преобразований.

Доказательство. В силу предыдущей теоремы нужно только показать,что кривые из разных классов не могут быть переведены друг в друга проективным преобразованием.Это следует сразу из того,что прямые переходят в прямые и что ранг матрицы сохраняется.

Замечание. Как мы уже видели,аффинное преобразование это проективное, переводящее несобственную прямую в несобственную и ограниченное на собственные точки.Таким образом,проективные классы могут содержать несколько аффинных. Именно,овал это эллипс,гипербола и парабола,мнимый овал мнимый эллипс, различные прямые параллельные или пересекающиеся прямые,аналогично для мнимых.При этом эллипс овал,не пересекающий несобственную прямую,гипербола овал,пересекающий несобственную прямую,парабола овал,касающийся несобственной прямой.

141

ЛЕКЦИЯ22.ВЕКТОР-ФУНКЦИЯ

§77.Векторная функция.Предел и непрерывность

Выберем на прямой,на плоскости или в пространстве точки X и Y .Будем обозначать через %(X, Y ) расстояние между этими точками.Будем говорить,что точка X стремится к фиксированной точке X0 ,если %(X, X0) ! 0.

Определение. Пусть G любое множество точек на прямой,плоскости или в пространстве.Говорят,что на множестве G задана вектор-функция f ,если каждой точке X этого множества сопоставлен вектор f(X).

Для вектор-функций,так же,как и для скалярных,вводится понятие предела.

Определение. Говорят,что вектор a является пределом функции f(X) при X ! X0 ,если |f(X) − a| ! 0 при X ! X0 .

Обозначение. X!X0	или	f(X)	!	a	при	X	!	0 .
lim f(X) = a								X
Имеют место теоремы о пределах,аналогичные теоремам о пределах для ска-
лярных функций.
Теорема77.1. Если f(X) и g(X) вектор-функции,а						λ(X) скалярная функция,
и f(X) ! a, g(X) ! b, λ(X) ! µ при X ! X0 ,то

f(X) ± g(X) ! a ± b, λ(X)f(X) ! µa, [f(X), g(X)] ! [a, b], (f(X), g(X)) ! (a, b).

Доказательство. Теорема доказывается так же,как и аналогичная теорема для скалярных функций.Докажем предпоследнее утверждение.Здесь воспользуемся неравенством

|[c, d]| = |c||d|| sin '| |c||d|,

которое выполняется для произвольных векторов c, d.

|[f(X), g(X)] − [a, b]| = |[f(X) − a, g(X)] + [a, g(X) − b]|

|f(X) − a||g(X)| + |a||g(X) − b|.

Отсюда следует,что |[f(X), g(X)] − [a, b]| ! 0 при X ! X0 ,т.е.что [f(X), g(X)] !

[a, b].

Определение. Вектор функция f(X) называется непрерывной в точке X0 ,если f(X) ! f(X0) при X ! X0 .

Утверждение. Пусть f(X) и g(X) вектор-функции,непрерывные в точке X0 , а λ(X) скалярная функция,непрерывная в этой точке.Тогда вектор-функции

f(X) ± g(X), λ(X)f(X), [f(X), g(X)],

а также скалярная функция (f(X), g(X)) непрерывны в точке X0 . Доказательство. Это утверждение сразу же следует из теоремы о свойствах пределов.

142

§78.Производная и дифференциал вектор-функции скалярного аргумента

Определение. Пусть f(t) вектор-функция,определенная на отрезке			[a, b].Если
существует предел отношения
f(t0 + h) − f(t0)
	h
при h ! 0,то он называется производной вектор-функции f в точке t0			и обознача-
ется f0(t0).

Определение. Вектор-функция f = f(t) называется дифференцируемой в точке t0 , если ее приращение в точке t0

f(t0) = f(t0 + h) − f(t0)

представимо в виде

f(t0) = ch + "(t0, h)h,

где "(t0, h) ! 0 при h ! 0.

При этом линейная вектор-функция ch называется дифференциалом функции f(t) в точке t0 и обозначается df = ch.

Следовательно, f = df + "(t0, h)h.

Если вектор-функция дифференцируема в точке,то она непрерывна в этой точке.Действительно,очевидно,что при h ! 0 дифференциал df = ch ! 0,а следовательно,и f ! 0.

Теорема78.1. Вектор-функция f дифференцируема в точке t0 тогда и только тогда,когда она имеет производную в этой точке.

Доказательство. Если вектор-функция дифференцируема в точке t0 ,то она имеет производную в этой точке,и производная равна c:

lim

f(t0 + h) − f(t0)

= lim

f

= lim(c + "(t0, h)) = c.

h

h!0

h

h!0

h!0

Обратно,если существует производная f0(t) = lim

f

,положим

h!0

h

"(t0, h) =

f(t0)

− f0(t0).

h

Тогда

f = f0(t0)h + "(t0, h)h,

где lim "(t0, h) = 0.Значит,

f(t) дифференцируема в точке t0 и df = f0(t0)h.

h!0

Обозначим независимую переменную h через dt,тогда

df = f0dt, f0

=

df

.

dt

Кроме того, f

= df + "(t0, h)h.

Пусть теперь t = t(s),причем функция

t(s) дифференцируема в точке s0 и

t0 = t(s0).Тогда,обозначив

s = s0 + h,получим

f

= ft

t

+

"(t0, t) t

.

h

h

h

143

Так как t ! 0 при h ! 0,то полагая "(t0, 0) = 0 (вообще говоря,векторфункция "(t0, h) не определена при h = 0,мы можем доопределить ее в нуле произ-

вольным образом,обычно полагают			"(t0, 0) = 0),получаем
	lim		"(t0,		t)		t	= 0.
			h
	h!0
В самом деле,из существования производной функции t(s)									в точке s0 следует ее
непрерывность в этой точке.А значит,при						h ! 0 t = t(s0 + h) − t(s0) ! 0.При
h = 0 имеем	t = 0,следовательно,функция							t непрерывно зависит от h,откуда
получаем,что	lim "(t0, t) = 0.
	h!0				f
Следовательно,производная f0		= lim					существует,и f0		= f0t0 .
	s		h!0		h			s	t s

Таким образом,как и в случае скалярных функций,получаем инвариантность

записи первого дифференциала:как для независимой переменной s,так и для зависимой переменной t имеем

df = ft0dt, df = fs0ds.

Для вектор-функций выполняются правила дифференцирования,аналогичные правилам дифференцирования скалярных функций.

Теорема78.2. Если f(t) и g(t) дифференцируемые в точке t0 вектор-функции, а λ(t) дифференцируемая в точке t0 скалярная функция,то функции

λ(t)f, f(t) ± g(t), [f(t), g(t)], (f(t), g(t))

дифференцируемы в точке t0 ,причем

(λf)0 = λ0f + λf0,

(f ± g)0 = f0 ± g0,

[f, g]0 = [f0, g] + [f, g0], (f, g)0 = (f0, g) + (f, g0).

Доказательство. Теорема доказывается аналогично формулам дифференцирования скалярных функций в анализе.Для примера докажем предпоследнюю формулу.

[f, g]0

= lim

[f(t0 + h), g(t0 + h)] − [f(t0), g(t0)]

=

h!0

h

= lim

[f(t0 + h), g(t0 + h)] [f(t0), g(t0 + h)] − [f(t0), g(t0)]

=

h!0

f(t0 + h)

f(t0)

h

g(t0 + h)

g(t0)

lim

0

0

h

−

, g(t0 + h)A

+ f(t0),

h

−

A

].

= h!0

= [f

, g] + [f, g

Определение. Производная вектор-функции f0 называется второй производной функции f(t) и обозначается f00 .

Аналогично определяются третья,четвертая и т.д.производные.

Определение. Вектор-функция,имеющая непрерывные производные до k-го порядка включительно на отрезке (a, b),называется k раз дифференцируемой на отрезке

(a, b).

Пусть e1, e2, e3 три некомпланарных вектора.Каждый вектор r допускает представление в виде

r = xe1 + ye2 + ze3,

144

где числа x, y, z определяются однозначно и называются координатами вектора r относительно базиса e1, e2, e3 .

Пусть r(t) вектор-функция,заданная на отрезке.Определим три скалярные функции x(t), y(t), z(t) условием

r(t) = x(t)e1 + y(t)e2 + z(t)e3.

Параметрическое задание кривой уравнениями

x = x(t), y = y(t), z = z(t)

эквивалентно заданию ее с помощью одного векторного уравнения

r = r(t) = x(t)e1 + y(t)e2 + z(t)e3,

где e1, e2, e3 единичные векторы,имеющие направления координатных осей x, y, z.

Теорема78.3. Вектор-функция r(t) непрерывна(дифференцируема)тогда и только тогда,когда функции x(t), y(t), z(t) непрерывны(дифференцируемы).

Доказательство. Достаточность очевидна.
Докажем необходимость.Для этого домножим равенство	r(t) = x(t)e1 + y(t)e2 +
z(t)e3 скалярно на вектор e10 ,перпендикулярный векторам	e2 и e3 .Получим

x(t)(e1, e01) = (r(t), e01).Отсюда видно,что непрерывность(дифференцируемость) вектор-функции r(t) влечет(дифференцируемость)функции x(t).Аналогично для функций y(t) и z(t).

Теорема78.4. Для вектор-функции имеет место формула Тейлора.Именно,если f(t) n раз дифференцируемая вектор-функция,то

		(					t)n
	f(t + t) = f(t) + tf0(t) + · · · +										(f(n)(t) + "(t, t)),
							n!
где |"(t,	t)| ! 0 при t ! 0.
Доказательство. В самом деле,
	f(t) = x(t)e1 + y(t)e2 + z(t)e3.
Но		(					t)n
	x(t + t) = x(t) + tx0(t) + · · · +									(x(n)(t) + "1(t, t)),
							n!
	y(t + t) = y(t) + ty0	(					t)n
		(t) + · · · +							(y(n)(t) + "2(t, t)),
							n!
	z(t + t) = z(t) + tz0	(					t)n
		(t) + · · · +						(z(n)(t) + "3(t, t)),
							n!
где "j(t,	t) ! 0 (j = 1, 2, 3) при	t ! 0.

Умножая эти равенства на e1, e2, e3 соответственно,складывая и замечая,что

f(k)(t) = x(k)(t)e1 + y(k)(t)e2 + z(k)(t)e3,

получаем формулу Тейлора для вектор-функции f(t).

145

§79.Интеграл вектор-функции

Понятие интеграла в смысле Римана для вектор-функции вводится буквально так же,как для скалярной функции.Интеграл обладает обычными свойствами.

Если f(t) непрерывная на отрезке a t b вектор-функция и a < c < b, то

Z b Z c Z b

f(t)dt = f(t)dt + f(t)dt.

a a c

Если µ постоянная,то

Z b Z b

µf(t)dt = µ f(t)dt.

a a

Если r постоянный вектор,то

Z b Z b

(r, f(t))dt = r, f(t)dt

a a

и	Zab[r, f(t)]dt = r, Zab f(t)dtA .
	Имеет место формула дифференцирования интеграла с переменным верхним
пределом			Za	x
		d
				f(t)dt = f(x).
		dx

§80.Годограф вектор-функции.Частные производные

Определение. Пусть f(X) вектор-функция,заданная на множестве G.Выберем произвольную точку O и для каждого X из множества G отложим вектор f(X) от точки O.Множество получающихся таким образом концов векторов называется

годографом,или траекторией вектор-функции.

В трехмерном пространстве годографом вектор-функции одного скалярного аргумента будет кривая,а годографом вектор-функции двух переменных поверхность.

Пример80.1. Пусть f : t ! (cos t, sin t), t 2 R .Годограф окружность единичного радиуса.

У разных вектор-функций может быть одна и та же траектория.Окружность единичного радиуса будет также траекторией вектор-функции g: t ! (cos 2t, sin 2t), t 2 R .

Рассмотрим вектор-функцию векторного аргумента f(X),где X = (t, u, v).

Определение. Частной производной вектор-функции f по переменной t в точке

(t0, u0, v0) называется производная вектор-функции f по t,когда u = u0, v = v0 ,т.е.

	@f	= ft = lim	f(t0 + h, u0, v0) − f(t0, u0, v0)	.
	@t
		h!0	h

Аналогично определяются частные производные по u и v.

146

Пусть r = r(u, v) вектор-функция двух скалярных аргументов, (u, v) точка некоторой плоской области D.

Пусть векторы e1, e2, e3 образуют базис пространства.Тогда справедливо равенство

r(u, v) = x(u, v)e1 + y(u, v)e2 + z(u, v)e3.

По определению частной производной имеем

@r

ru = @u = xu(u, v)e1 + yu(u, v)e2 + zu(u, v)e3,

@r

rv = @v = xv(u, v)e1 + yv(u, v)e2 + zv(u, v)e3.

Определение. Вектор-функция r(u, v) называется дифференцируемой в точке (u, v), если ее полное приращение в этой точке для любых u, v представимо в виде

p

r = r(u+ u, v+ v)−r(u, v) = ru(u, v) u+rv(u, v) v+"(u, v, u, v) u2 + v2,

	где	"(u, v, u, v)
	lim				= 0.
	u!0, v!0	p u2 + v2

Определение. Главная линейная часть приращения ru(u, v) u + rv(u, v) v называется дифференциалом вектор-функции r и обозначается dr.

Положим u = du, v = dv,тогда будем иметь

dr = rudu + rvdv.

Частные производные второго порядка вектор-функции r(u, v) определяются

следующим образом:	@							@2r(u, v)
ruu =					ru(u, v) =						,
		@u						@u2
ruv =	@			ru(u, v) =			@2r(u, v)				,
	@v							@u@v
	@					@2r(u, v)
rvv =			rv(u, v) =						.
	@v							@v2

Дифференциал второго порядка имеет вид

d2r = d(dr) = d(rudu + rvdv) = ruudu2 + 2ruvdudv + rvvdv2.

Аналогично определяются частные производные вектор-функции более высоких порядков.

147

ЛЕКЦИЯ23.ЭЛЕМЕНТЫ ТЕОРИИ КРИВЫХ

§81.Понятие кривой

Определение. Пусть M произвольное множество точек пространства.Если каждой точке X множества M поставлена в соответствие некоторая точка f(X) пространства,то говорят,что задано отображение f множества M в пространство. Точка f(X) называется образом точки X . Точка X называется прообразом точки f(X).Множество f(M),состоящее из образов всех точек множества M ,называется образом множества M .

Определение. Отображение f множества M называтеся взаимно-однозначным,или одно-однозначным,или биекцией,если образы различных точек различны.

Пусть f взаимно-однозначное отображение.Тогда естественным образом определено отображение f−1 ,заданное на множестве f(M),которое каждой точке f(X) ставит в соответствие точку X ,т.е.ее прообраз при отображении f .

Определение. Отображение f−1 называется обратным к отображению f .

Определение. Отображение f множества M называется непрерывным,если для любой точки X из множества M и любого " > 0 существует δ > 0,такое,что для любой точки Y 2 M расстояние между точками f(Y ) и f(X) меньше " как только расстояние между Y и X меньше δ .

Пусть f взаимно-однозначное и непрерывное отображение множества M .

Определение. Отображение f называется топологическим отображением,если отображение f−1 множества f(M) также непрерывно.

Множество M и его образ f(M) при топологическом отображении f называются

топологически эквивалентными,или гомеоморфными.

Определение. Множество γ точек пространства называется элементарной кривой, если оно является образом открытого отрезка прямой при топологическом отображении его в пространство.

Определение. Пусть γ элементарная кривая и a < t < b отрезок,образом которого при отображении f является кривая.Пусть x(t), y(t), z(t) координаты точки кривой,соответствующей точке t отрезка.Тогда уравнения

x = x(t), y = y(t), z = z(t)

называются уравнениями кривой γ в параметрической форме,или параметризацией кривой γ .

Считая x(t), y(t), z(t) координатами радиус-вектора r(t) соответствующей точки кривой γ ,получим вектор-функцию r(t), t 2 (a, b),годографом которой является данная кривая.

Пусть кривая γ задана вектор-функцией r(t), t 2 (a, b).Заменим параметр t параметром u с помощью соотношения t = g(u), u 2 ( ,β ),где функция g строго возрастает и непрерывна.Тогда получим новую параметризацию кривой γ : r = r(g(u)), u 2 ( ,β ).Тем самым,одна и та же кривая допускает различные параметризации.

Определение. Множество G точек пространства называется открытым,если для каждой точки X этого множества можно указать такое число " > 0 такое,что все точки пространства,расстояние которых от X меньше ",также принадлежат G.

148

Очевидно,что множество,состоящее из любой совокупности открытых множеств,также будет открытым.

Определение. Окрестностью точки X называется любое открытое множество,содержащее эту точку.

Определение. Множество M точек пространства называется связным,если не существует двух открытых множеств G0 и G00 ,разбивающих M на две части M0 и M00 ,одна из которых принадлtжала бы только G0 ,а другая только G00 .

Пример81.1. Парабола связное множество,гипербола несвязное множество.

Определение. Множество γ точек пространства называется простой кривой,если это множество связно и у каждой его точки X есть такая окрестность,что расположенная в ней часть γ является элементарной кривой.

Строение простой кривой в целом определяется следующей теоремой:

Теорема81.1. Простая кривая гомеоморфна отрезку или окружности.

Определение. Простая кривая,гомеоморфная окружности,называется замкнутой.

Определение. Окрестностью точки X на простой кривой γ называется общая часть кривой γ и некоторой пространственной окрестности точки X .

По определению,у каждой точки простой кривой есть окрестность,являющаяся элементарной кривой(рис. 1).В дальнейшем,говоря об окрестности точки кривой, будем иметь в виду такую элементарную окрестность.

Пусть простая кривая γ является образом открытого отрезка или окружности g при топологическом отображении f .Пусть X произвольная точка g и ! любая

ее окрестность.Тогда образ ! при отображении f	является окрестностью точки
f(X) на кривой γ .Обратно,любая окрестность точки	f(X) может быть получена
таким способом.

Определение. Отображение множества M в пространство называется локально топологическим,если у каждой точки этого множества есть окрестность,в которой отображение f топологическое.

Определение. Множество γ точек пространства называется общей кривой,если оно является образом простой кривой при локально топологическом отображении ее в пространство.

Определение. Отображение f1 простой кривой γ1 и отображение f2 простой кривой γ2 определяют одну и ту же общую кривую γ ,если между точками γ1 и γ2 может быть установлено топологическое соответствие,при котором образы соответствующих точек на этих кривых совпадают.

149

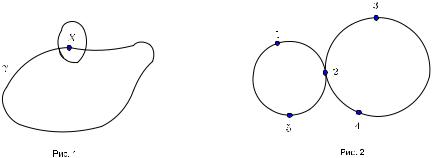
Пример81.2. На рисунке2изображена общая кривая.Ее можно представить как образ окружности при локально топологическом отображении двумя различными способами,которые с точки зрения данного определения дают различные кривые. Действительно,пусть точка движется по окружности.Тогда ее образ может двигаться по кривой,занимая последовательно положения1, 2, 3, 4, 2, 5,а может и в следующем порядке: 1, 2, 4, 3, 2, 5.Отображения,соответствующие этим обходам, определяют различные общие кривые,хотя как множества точек они совпадают.

Пусть общая кривая γ является образом при локально топологическом отображении f в пространство простой кривой γ¯ .Окрестностью точки f(X) на кривой γ будем называть образ любой окрестности точки X на кривой γ¯ при отображении f . Так как отображение f в достаточно малой окрестности точки X является топологическим,то f(X) на γ имеет окрестность,являющуюся элементарной кривой.

Таким образом,исследование любой кривой“в малом”,т.е.в достаточно малой окрестности каждой ее точки,может быть сведено к исследованию элементарной кривой.

§82.Регулярная кривая

Определение. Кривая γ называется регулярной,или k раз дифференцируемой,если у каждой точки этой кривой есть окрестность,допускающая регулярную параметризацию,т.е.задание уравнениями в параметрической форме

x = x(t), y = y(t), z = z(t),

где x, y, z регулярные( k раз непрерывно дифференцируемые функции).При k = 1 кривая называется гладкой.

Определение. Вещественная функция f(x) называется аналитической в открытом множестве D R,если для любой точки x0 2 D f(x) представима в виде

X1

f(x) = an(x − x0)n = a0 + a1(x − x0) + a2(x − x0)2 + a3(x − x0)3 + . . . ,

n=0

где коэффициенты a0, a1, a2, a3, . . . вещественные и ряд сходится к f(x) для любого x из некоторой окрестности x0 .

Определение. Кривая называется аналитической,если она в достаточно малой окрестности каждой своей точки допускает аналитическую параметризацию(функции x, y, z аналитические).

В дальнейшем будем рассматривать только регулярные кривые.

Кривая в окрестности каждой точки может быть задана параметрическими уравнениями вида

x = x(t), y = y(t), z = z(t), a < t < b.

(82.1)

Возникает вопрос,когда уравнения(82.1)определяют регулярную кривую?

Теорема82.1. Если x(t), y(t) и z(t) регулярные функции,удовлетворяющие условию

x02(t) + y02(t) + z02(t) > 0, при a < t < b,

то система равенств

x = x(t), y = y(t), z = z(t) (a < t < b)

150