geometry24

Определение. Пусть прямая в аффинной системе координат задана уравнением

F (x, y)	= Ax + By + C = 0. Положительной полуплоскостью называется мно-
жество	точек (x, y),удовлетворяющих неравенству F (x, y) > 0. Отрицательной

полуплоскостью называется множество точек (x, y),удовлетворяющих неравенству

F (x, y) < 0:

F+ = {(x, y)|F (x, y) > 0}, F− = {(x, y)|F (x, y) < 0}.

Теорема21.3. Если точки P и Q лежат в одной полуплоскости,то и весь отре-

зок P Q лежит в ней.Если

P и Q лежат в разных полуплоскостях,то отрезок

P Q пересекает данную прямую.Тем самым,множества

F+ и F− действительно

являются полуплоскостями с границей,проходящей по данной прямой.

Доказательство. Пусть P (xP , yP ), Q(xQ, yQ).Координаты точки

X отрезка P Q

равны

x =

µxP + λxQ

, y =

µyP + λyQ

,λ, µ > 0.

µ + λ

µ + λ

Тогда

F (x, y) = A

µxP + λxQ

+ B

µyP + λyQ

+ C

µ + λ

=

1

[µF (xP , yP ) + λF (xQ, yQ)] ,

µ + λ

µ + λ

µ + λ µ + λ

причем множитель строго положителен.Значит,если

P и Q принадлежат F+ или

F− ,то есть F (xP , yp) и F (xQ, yQ) одного знака,то и

F (x, y) того же знака.Если же

F (xP , yP ) и F (xQ, yQ) разных знаков,то при µ = |F (xP ,yP )| , λ =

|F (xQ,yQ)| соответ-

1

1

ствующее F (x, y) обращается в нуль.

Замечание. Если отложить вектор (A, B) от некоторой точки (x0, y0) на прямой,то его конец окажется в F+ .Действительно,

A(x0 + A) + B(y0 + B) + C = (Ax0 + By0 + C) + A2 + B2 = A2 + B2 > 0.

41

ЛЕКЦИЯ7.ПРЯМЫЕ И ПЛОСКОСТИ

§22.Пучки прямых на плоскости

Определение. Множество всех прямых на плоскости,проходящих через фиксированную точку,называется собственным пучком прямых,а сама точка центром пучка.

Множество всех прямых на плоскости,параллельных данной прямой,называется

несобственным пучком прямых.

Замечание. Терминология связана с проективной геометрией.

Теорема22.1. Прямая l с уравнением F = Ax + By + C = 0 принадлежит(собственному или несобственному)пучку,задаваемому парой несовпадающих прямых

l1 и l2 с уравнениями F1 = A1x + B1y + C1 = 0 и F2 = A2x + B2y + C2 = 0 тогда и только тогда,когда ее уравнение является нетривиальной линейной комбинацией

уравнений l1 и l2 : F = F1 + βF2 .

Доказательство. Пусть в случае собственного пучка прямые l1 и l2 пересекаются в точке P0(x0, y0).Прямая l принадлежит этому пучку тогда и только тогда,когда

P0 2 l.

В случае несобственного пучка прямые l1 и l2 параллельны.Прямая l принадлежит этому пучку тогда и только тогда,когда она им параллельна. Доказательство необходимости. Пусть P (xP , yP ) произвольная точка прямой l,принадлежащей пучку.В случае собственного пучка выберем P так,чтобы она не совпадала с P0 .Рассмотрим уравнение

˜ −

F (x, y) = F2(xP , yP )F1 F1(xP , yP )F2 = 0.

Это уравнение степени не выше первой:

˜ ˜ ˜ ˜

F (x, y) = Ax + By + C.

При этом F1(xP , yP ) и F2(xP , yP ) не могут одновременно равняться нулю,иначе обе прямые l1 и l2 проходили бы через P .

В случае собственного пучка векторы (A1, B1) и (A2, B2) неколлинеарны,следо-

˜ ˜
вательно (A, B) 6= 0.
В случае несобственного пучка векторы (A1, B1) и (A2, B2) коллинеарны.Пред-
положим,что
˜ ˜	, yP )A1		− F1(xP , yP )A2, F2(xP , yP )B1 − F1(xP , yP )B2) = 0.
(A, B) = (F2(xP
Поскольку уравнение		˜
		F (x, y) = 0 имеет решение(ему удовлетворяют координаты
точки P ,например),то		˜	= 0.Тогда получаем,что уравнения F1(x, y) = 0 и
		C

F2(x, y) = 0 пропорциональны и задают одну прямую,что противоречит условию. Тем самым,в обоих случаях имеем уравнение первой степени,которое задает

прямую.

Вслучае собственного пучка,подставляя в это уравнение координаты точек P

иP0 ,получаем,что прямая проходит через эти две точки.

Вслучае несобственного пучка это уравнение прямой,проходящей через точку P и параллельной прямым l1 и l2 .

42

В обоих случаях это уравнение прямой l.По теореме20.1получаем

˜	(xP , yP ))F1	+ (−λF1(xP , yP ))F2	= 0, λ 6= 0.
F = λF = (λF2

Доказательство достаточности. В случае собственного пучка

F (x0, y0) = F1(x0, y0) + βF2(x0, y0) = 0.

Следовательно, l проходит через центр пучка.

В случае несобственного пучка F	=	F1 + βF2 ,значит,вектор (A, B) =
(A1, B1) + β(A2, B2) коллинеарен (A1, B1)		и (A2, B2).Раз это уравнение прямой,
то (A, B) 6= 0.Значит, lkl1kl2 ,и прямая	l принадлежит пучку.

Следствие22.1. Три прямые Aix + Biy + Ci = 0, i = 1, 2, 3 принадлежат одному и тому же пучку тогда и только тогда,когда

"	A1	B1	C1	"
"	A2	B2	C2	"	= 0.
"				"
"				"
"	A3	B3	C3	"
"				"

§23.Прямая на плоскости в прямоугольной системе координат

Лемма23.1. Вектор n = (A, B) нормальный вектор прямой Ax + By + C = 0.

Доказательство. Векторы,параллельные прямой,задаются уравнением(см.лемму21.1) A + Bβ = 0 или,так как координаты прямоугольные, (n, ( ,β )) = 0.

Теорема23.1. Расстояние от точки P (x0, y0) до прямой l,заданной уравнением

Ax + By + C = 0,равно

%(P, l) = |Axp0 + By0 + C|. A2 + B2

Доказательство. Пусть P1(x1, y1) произвольная точка на прямой, ' угол между векторами PP1 и n нормальным вектором прямой.Тогда

%(P, l) =

P P

1| · |

cos '

=

|(PP1, n)|

=

|A(x0

− x

1) + B(y0 − y1)|

=

|

|

|n|

pA2 + B2

=

|(Ax0 + By0

+ C) − (Ax

1 + By1 + C)|

=

|Ax0

+ By0 +

C|

.

pA2 + B2

pA2 + B2

Определение. Уравнение прямой Ax+By+C = 0 называется нормированным,если A2 + B2 = 1,то есть нормальный вектор n = (A, B) имеет единичную длину.

Замечание. Каждая прямая имеет два нормированных уравнения.Они получаются из уравнения прямой Ax + By + C = 0 делением на длину нормального

вектора:
±	p	A	x +	p	B	y +	p	C	= 0.
		A2 + B2			A2 + B2			A2 + B2

Определение. Для нормированного уравнения прямой F (x, y) = Ax + By + C = 0 величина F (x, y) называется отклонением точки (x, y) от прямой.

43

Имеем для нормированного уравнения
F (x, y) = "	·	%((x, y), l), " =		+1,	если	(x, y) 2 F+,
				−1,	если	(x, y) 2 F−.

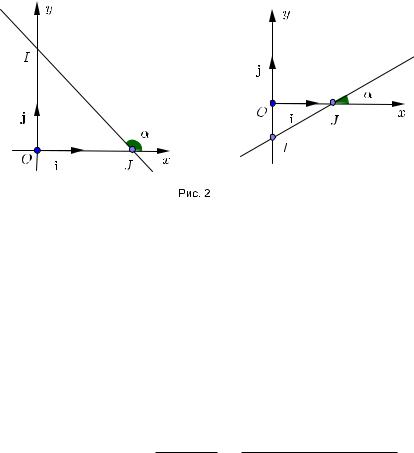
Выясним геометрический смысл коэффициентов k и b в уравнении прямой на плоскости с угловым коэффициентом в прямоугольной системе координат.

Прямая l,заданная уравнением y = kx + b,пересекает ось ординат в точке I с координатами (0, b).

Определение. Углом наклона прямой l к оси абсцисс на ориентированной плоскости называется наименьший угол ,отсчитываемый в положительном направлении,на который нужно повернуть ось Oi вокруг точки пересечения J прямой с данной осью, чтобы она совпала с прямой l.

Ясно,что 0 < .

Точка пересечения прямой l и оси абсцисс J имеет координаты (x0, 0),где x0 =

−b/k.Если b > 0, x0 < 0 или b < 0, x0 > 0,то угол острый( tg > 0),если b > 0, x0 > 0 или b < 0, x0 < 0,угол тупой( tg < 0).

Тангенс угла наклона прямой l к оси абсцисс находится как отношение катетов OI и OJ прямоугольного треугольника OIJ ,взятое со знаком“минус”,если b и x0 одного знака,и“плюс”,если b и x0 разных знаков.Таким образом, tg = k.

Найдем угол между двумя прямыми на плоскости.Пусть в прямоугольной си-

стеме координат прямые имеют уравнения A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0. Тогда косинус угла между прямыми равен модулю косинуса угла между их нормаль-

ными векторами n1 и n2 :

cos ' =	|(n1, n2)|		=		|A1A2	+ B	1B2|	.
	|n1| · |n2|			pA12 + B12 · pA22 + B22

§24.Различные виды уравнений плоскости

Параметрическое уравнение плоскости

Пусть a и b два линейно независимых вектора,параллельных плоскости.Тогда любой вектор плоскости однозначно представляется в виде их линейной комбинации.Поэтому,взяв произвольную точку плоскости с радиус-вектором r0 ,получим параметрические уравнения плоскости

r = r0 + sa + tb,

44

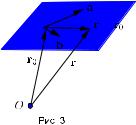
где s и t параметры, r радиус-вектор произвольной точки плоскости.

Общее уравнение плоскости

Теорема24.1. Плоскости в пространстве определяются уравнениями первой степени от трех переменных.Обратно:любое уравнение первой степени от трех переменных определяет плоскость.

Доказательство. Из параметрического уравнения плоскости ясно,что точка с радиус-вектором r лежит в рассматриваемой плоскости тогда и только тогда,когда векторы r − r0, a и b компланарны,то есть линейно зависимы,иначе говоря, их смешанное произведение равно нулю: (r − r0, a, b) = 0.Переходя к аффинным координатам векторов,получаем уравнение

"

x − x0 y − y0 z − z0

"

a1

a2

a3

= 0.

"

b1

b2

b3

"

"

"

Обозначая

"

"

"

"

"

"

A =

"

a2 a3

" , B =

"

a3 a1

"

, C = "

a1 a2

"

,

b2 b3

b3

b1

b1 b2

"

"

"

"

x0

"

z0

"

"

"

"

"

"y0

"

"

"

"

"

"−

−"

−

"

D =

−

(Ax0 + By0 + Cz0) =

a1

a2

a3

"

,

"

b1

b2

b3

"

"

"

преобразуем уравнение к виду

"

"

"

"

"

"

A(x − x0) + B(y − y0) + C(z − z0) = 0,

Ax + By + Cz + D = 0.

Поскольку a и b неколлинеарны,то (A, B, C) 6= 0.Увидеть это можно,например, из следующего рассуждения.Допустим, ai и bj координаты некоторых векторов a0 и b0 относительно ортонормированного базиса i, j, k положительной ориентации.

Эти тройки чисел ненулевые непропорциональные,так что				a0	и b0 неколлинеарны.
Значит,	[a0	6	.Но координаты этого вектора в базисе			в точности равны
		, b0] = 0		i, j, k
(A, B, C).
Итак, Ax + By + Cz + D = 0 уравнение первой степени.
Рассмотрим теперь произвольное уравнение первой степени Ax + By + Cz + D =
0.Тогда один из коэффициентов при переменных,например,					A,не равен нулю.

Рассмотрим точку M (−D/A, 0, 0) и векторы a = (−B, A, 0) и b = (−C, 0, A).Эти

векторы неколлинеарны,поэтому уравнение			A "
"	−C	0
"	D/A	y	z	"	= 0
	x + B	A	0
"	−			"
"				"
"				"
"				"

задает плоскость,проходящую через точку M параллельно a и b.Но если мы раскроем определитель,то получим в точности исходное уравнение.

45

Определение. Уравнение вида

Ax + By + Cz + D = 0, где A2 + B2 + C2 6= 0

называется общим уравнением плоскости.

Уравнение плоскости в отрезках

Лемма24.1. Вектор ( ,β,γ ) параллелен плоскости Ax + By + Cz + D = 0 тогда и только тогда,когда A + βB + γC = 0.

Доказательство. Лемма доказывается аналогично случаю прямой на плоскости.

Определение. Общее уравнение плоскости называется полным,если все его коэффициенты A, B, C и D отличны от нуля.В противном случае уравнение называется

неполным.

Рассмотрим все возможные неполные уравнения.

1)Если D = 0,то плоскость проходит через начало координат,поскольку точка (0, 0, 0) принадлежит плоскости.

2)Если A = 0,то уравнение By + Cz + D = 0 определяет плоскость,параллельную вектору e1 ,поскольку координаты векторов ( ,β,γ ),параллельных плоскости, удовлетворяют уравнению βB + γC = 0.Следовательно,вектор (1, 0, 0) параллелен

плоскости.Аналогично,если	B = 0,то уравнение Ax + Cz + D = 0 задает плос-
кость,параллельную вектору	e2 ,а если C = 0,то получаем уравнение плоскости

Ax + By + D = 0,которая параллельна вектору e3 .

3)Если A = B = 0,то уравнение Cz + D = 0 определяет плоскость,параллельную плоскости Oe1e2 ,поскольку эта плоскость параллельна векторам (1, 0, 0) и (0, 1, 0).Аналогично уравнения By + D = 0 и Ax + D = 0 определяют плоскости,

параллельные плоскостям Oe1e3 и Oe2e3 .

4)Если A = B = D = 0,то уравнение

Cz = 0 определяет плоскость Oe1e2

(плоскость,параллельную плоскости

Oe1e2 и проходящую через начало координат).

Аналогично рассматриваются случаи A = C = D = 0 и B = C = D = 0.

Рассмотрим теперь полное уравнение плоскости,запишем его в виде

x

y

z

+

+

= 1,

иначе

−D/A

−D/B

−D/C

x

y

z

D

D

D

+

+

= 1, a = −

, b = −

, c = −

.

a

b

c

A

B

C

Уравнение такого вида называется уравнением прямой в

отрезках.

Коэффициенты a, b и c в этом уравнении равны вели-

чинам отрезков,которые плоскость отсекает на осях Ox, Oy

и Oz соответственно.Действительно,для того чтобы найти,

например,точку пересечения плоскости с осью Ox,нужно

положить в уравнении плоскости y = z = 0 и найти x.По-

лучим x = a.

Векторное уравнение плоскости

Определение. Нормальным вектором плоскости называется любой ненулевой вектор,ортогональный данной плоскости.

46

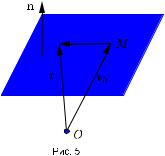
Теорема24.2. Плоскость с нормальным вектором n,проходящая через точку M с радиус-вектором OM = r0 ,задается векторным уравнением

(r, n) + D = 0,

(24.1)

где D = −(r0, n).

Доказательство. Эта теорема доказывается точно так же,как и аналогичная теорема для прямой на плоскости.

Замечание. В полной аналогии со случаем прямой на плоскости плоскость в пространстве,заданная уравнением F (x, y, z) = Ax + By + Cz + D = 0,разбивает пространство на два полупространства

F+ = {(x, y, z)|F (x, y, z) > 0}, F− = {(x, y, z)|F (x, y, z) < 0}.

Вектор (A, B, C) опять указывает на F+ .

47

ЛЕКЦИЯ8.ПЛОСКОСТИ И ПРЯМЫЕ В ПРОСТРАНСТВЕ

§25.Взаимное расположение плоскостей в пространстве

Теорема25.1. Плоскости 1 и 2 ,заданные уравнениями A1x+ B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0 параллельны тогда и только тогда,когда векторы

(A1, B1, C1) и (A2, B2, C2) коллинеарны,то есть			A1	=	B1	=	C1 .Эти плоскости
совпадают тогда и только тогда,когда		= B1	A2		B2		C2
	A1		= C1	= D1 .
	A2	B2	C2		D2

Доказательство. Докажем сначала утверждение о параллельности плоскостей. Достаточность. Из условия пропорциональности следует,что множества ре-

шений уравнений A1 + B1β + C1γ = 0 и A2 + B2β + C2γ = 0 совпадают,то есть плоскостям параллельны одни и те же множества векторов,а значит,плоскости па-

раллельны.

Необходимость. Один из коэффициентов первого уравнения должен быть отличен от нуля.Без ограничения общности,это A1 .Тогда по лемме24.1,неколлинеарные векторы (−B1, A1, 0) и (−C1, 0, A1) параллельны плоскости 1 и,таким образом, образуют базис плоскости.Поскольку 1k 2 , то

A2 · (−B1) + B2 · A1 + C2 · 0 = 0, A2 · (−C1) + B2 · 0 + C2 · A1 = 0,

откуда

A1 = B1 , A1 = C1 .

A2 B2 A2 C2

Перейдем ко второй эквивалентности.

Достаточность очевидна,поскольку умножение уравнения на ненулевой множитель не изменяет его множества решений.

Необходимость. По первой части A2 = λA1 , B2 = λB1 , C2 = λC1 .Пусть (x0, y0, z0) произвольная точка совпадающих плоскостей,так что

0 = λ(A1x0 + B1y0 + C1z0 + D1) − (A2x0 + B2y0 + C2z0 + D2) = λD1 − D2.

Пропорциональность четверок установлена.

Следствие25.1. Плоскости 1 и 2 (в обозначениях предыдущей теоремы)пересекаются по прямой тогда и только тогда,когда векторы (A1, B1, C1) и (A2, B2, C2) неколлинеарны.

§26.Пучки и связки плоскостей

Определение. Собственным пучком плоскостей называется множество всех плос-

костей,проходящих через фиксированную прямую. Несобственным пучком плоскостей называется множество всех плоскостей,параллельных данной плоскости.

Теорема26.1. Плоскость F = Ax + By + Cz + D = 0 принадлежит пучку плоскостей,определяемому двумя несовпадающими плоскостями F1 = A1x + B1y + C1z +

D1 = 0 и F2 = A2x+B2y+C2z+D2 = 0 тогда и только тогда,когда F = 1F1 + 2F2 , где 1 и 2 не равны одновременно нулю.

Доказательство. Утверждение теоремы доказывается полностью аналогично случаю прямых.

48

Определение. Собственной связкой плоскостей называется множество всех плос-

костей,проходящих через фиксированную точку(сама точка называется центром связки). Несобственной связкой плоскостей называется множество всех плоскостей, параллельных данной прямой.

Утверждение. Общее уравнение связки плоскостей с центром в точке (x0, y0, z0) имеет вид

A(x − x0) + B(y − y0) + C(z − z0) = 0.

Доказательство. Для того чтобы плоскость Ax + By + Cz + D = 0 принадлежала связке,необходимо и достаточно выполнения единственного условия

Ax0 + By0 + Cz0 + D = 0.

Это условие можно переписать следующим образом:

D = −Ax0 − By0 − Cz0.

подставим найденное значение D в уравнение плоскости и получим уравнение связки плоскостей:

A(x − x0) + B(y − y0) + C(z − z0) = 0.

Утверждение. Общее уравнение несобственной связки плоскостей имеет вид

−(Bβ + Cγ)x + B y + C z = 0,

если ( ,β,γ ) координаты направляющего вектора прямой,которой параллельны плоскости связки, 6= 0.

Доказательство. Коэффициенты уравнения плоскости

Ax + By + Cz + D = 0

по лемме24.1должны удовлетворять соотношению A + Bβ + Cγ = 0,откуда(при6= 0)получаем A = −(Bβ + Cγ)/ ,что сразу дает требуемое.

§27.Плоскость в прямоугольной системе координат

Утверждение. Рассмотрим плоскость Ax + By + Cz + D = 0.Тогда вектор n = (A, B, C) является нормальным вектором плоскости.

Доказательство. Вектор ( ,β,γ ) параллелен плоскости тогда и только тогда,когда

0 = A + Bβ + Cγ = (n, ( ,β,γ )),

то есть вектор n перпендикулярен любому вектору плоскости.

Теорема27.1. Пусть плоскость имеет уравнение Ax+By+ Cz + D = 0,а точка P cкоординатами (x0, y0, z0) произвольная точка.Тогда

%(P, ) = |Ax0p+ By0 + Cz0 + D|. A2 + B2 + C2

Доказательство. Пусть P1(x1, y1, z1) произвольная точка,а угол ' угол между векторами PP1 и n нормальным вектором .Тогда

49

%(P, ) =

P

P

||

cos '

=

|(P1P, n)|

=

|A(x0 − x1) +

B(y0 − y1) +

C(z0 − z1)|

=

|

1

|

|n|

pA2 + B2 + C2

=

|(Ax0 + By0

+ Cz0

+ D) − (Ax1 + By1 + Cz1

+ D)|

=

|Ax0 + By0 + Cz0 + D|

.

pA2 + B2 + C2

pA2 + B2 + C2

Углы между плоскостями,нормированное уравнение и отклонение также определяются и вычисляются полностью аналогично случаю прямых на плоскости.

§28.Прямая в пространстве

Текущий вектор точки на прямой запишется в виде r = r0 + at,где r0 радиус-

вектор начальной точки,а a направляющий вектор прямой(рис. 2).

Если координаты вектора a равны ( ,β,γ ),то получаем параметрические урав-

нения прямой в пространстве

8

< x = x0 + t

: y = y0 + βt z = z0 + γt

Исключая параметр t,получаем канонические уравнения

x − x0	=	y − y0	=	z − z0	.
		β		γ

В пространстве прямая определяется уже двумя линейными уравнениями,иными словами,прямая является пересечением двух плоскостей.Действительно, a 6= 0, допустим,что 6= 0 и возникают две пересекающиеся плоскости

β(x − x0) − (y − y0) = 0 γ(x − x0) − (z − z0) = 0.

Обратно,пусть имеем пересечение двух плоскостей или систему линейных уравнений

	A1x + B1y + C1z + D1	= 0	(28.1)
	A2x + B2y + C2z + D2 = 0,

где векторы (A1, B1, C1) и (A2, B2, C2) неколлинеарны.

Утверждение. В этом случае координаты направляющего вектора прямой,по которой пересекаются плоскости,равны

"

B1

C1

"

"

C1

A1

"

"

A1

B1

"

( ,β,γ ) =

"

B2

C2

"

,

"

C2

A2

"

,

"

A2

B2

"

"

"

"

"

"

" .

"

"

"

"

"

"

Доказательство. Указанный вектор не является векторным произведением,так как система координат не обязана быть прямоугольной.

Надо доказать,что указанный вектор ненулевой и что он параллелен обеим плоскостям.

Предположим,что данный вектор нулевой.Тогда

B1 = C1 , C1 = A1 , A1 = B1 ,

B2 C2 C2 A2 A2 B2

50