geometry24

или имеется два асимптотических направления (1, 0) и (0, 1),если a11 = a22 = 0, a12 6= 0 (эти асимптотические направления находятся из уравнения 2a12xy = 0).

В противном случае кривая асимптотических направлений не имеет. Эллиптические кривые не имеют асимптотических направлений,параболические

кривые имеют одно асимптотическое направление,а гиперболические кривые имеют два асимптотических направления.

Для гиперболы асимптотические направления это направления ее асимптот (отсюда и название),для пары пересекающихся прямых это направления самих прямых.

Для параболы единственным асимптотическим направлением является направление ее оси,а для пары параллельных или совпадающих прямых направление этих прямых.

81

ЛЕКЦИЯ13.ДИАМЕТРЫ КРИВОЙ ВТОРОГО ПОРЯДКА

§44.Диаметры

Рассмотрим непустую кривую второго порядка F ,заданную в некоторой аффинной системе координат уравнением

F (x, y) = a11x2 + 2a12xy + a22y2 + 2a1x + 2a2y + a0 = 0.

Лемма44.1. Если направление ( ,β ) неасимптотическое,то хотя бы одно из чисел

a11 + a12β, a12 + a22β

отлично от нуля.

Доказательство. Предположим,что

a11 + a12β = 0, a12 + a22β = 0.

Домножим первое из этих равенств на ,второе на β и сложим полученные уравнения:

(a11 + a12β) + β(a12 + a22β) = a11 2 + 2a12 β + a22β2 = q( ,β ) = 0.

Тем самым,направление ( ,β ) асимптотическое,что противоречит условию.

Пусть l прямая неасимптотического направления,заданная параметрическими уравнениями

x = x0 + t, y = y0 + βt.

Найдем точки пересечения F и l,для этого подставим параметрические уравнения прямой в уравнение кривой:

a11(x0 + t)2 + 2a12(x0 + t)(y0 + βt) + a22(y0 + βt)2 + 2a1(x0 + t) + 2a2(y0 + βt) + a0 = 0

или

F2t2 + 2F1t + F0 = 0,

где

F2 = q( ,β ) = a11 2 + 2a12 β + a22β2,

F1 = (a11x0 + a12y0 + a1) + β(a12x0 + a22y0 + a2),

F0 = F (x0, y0).

Теорема44.1. Середины хорд кривой F данного неасимптотического направления ( ,β ) лежат на прямой

(a11x + a12y + a1) + β(a12x + a22y + a2) = 0,

или

	1 @F			(x, y) +	1 @F			(x, y)β = 0.
	2 @x				2 @y

Доказательство. Для нахождения общих точек кривой второго порядка и прямой неасимптотического уравнения мы имеем уравнение второй степени.Это уравнение

82

имеет два решения(возможно,совпадающих)либо не имеет решений.Предположим, что прямая l пересекает кривую F в точках t1 и t2 (возможно, t1 = t2 ).Пусть точка (x0, y0) середина хорды кривой,соединяющей эти точки.Тогда значение t0 = 0,которому соответствует данная точка,можно найти по формуле Виета для квадратного уравнения:

0 = t0 = t1 + t2 = −F1 , F1 = 0. 2 F2

Таким образом,середины хорд кривой данного неасимптотического направления лежат на кривой

(a11x + a12y + a1) + β(a12x + a22y + a2) = 0.

По лемме44.1это уравнение первой степени,следовательно,оно задает прямую.

Определение. Прямая ( a11 + βa12)x + ( a12 + βa22)y + ( a1 + βa2) = 0 называется диаметром кривой второго порядка

F = a11x2 + 2a12xy + a22y2 + 2a1x + 2a2y + a0 = 0,

сопряженным данному неасимптотическому направлению ( ,β ). Теорема44.2. Любой диаметр проходит через все центры кривой.

Доказательство. Пусть (x0, y0) произвольный центр кривой второго порядка. Тогда

a11x0 + a12y0 + a1 = 0, a12x0 + a22y0 + a2 = 0.

Умножим первое уравнение на ,а второе на β и сложим полученные равенства:

(a11 + a12β)x0 + (a12 + a22β)y0 + (a1 + a2β) = 0.

Тем самым,точка (x0, y0) лежит на диаметре.

§45.Сопряженные диаметры и направления

Теорема45.1. Диаметр,сопряженный данному неасимптотическому направлению ( ,β ) имеет направление ( , β ):

(a11 + a12β) + (a12 + a22β)β = ( ,β )A		= 0.	(45.1)
	β

Доказательство. Сопряженный к ( ,β ) диаметр имеет уравнение

(a11x + a12y + a1) + β(a12x + a22y + a2) = 0.

Направление (u, v) прямой ax + by + c = 0,как мы знаем,должно обнулять однородную часть: au + bv = 0.В нашем случае

(a11 + a12β ) + β(a12 + a22β ) = ( ,β )A = 0.

β

Определение. Направления ( ,β ) и ( , β ),связанные уравнением(45.1),называются сопряженными относительно данной кривой второго порядка F .

83

Следствие45.1. Если направление ( , β ) не является асимптотическим,то сопряженным для ( , β ) будет направление ( ,β ).

Доказательство. Утверждение сразу следует из симметричности уравнения(45.1)транспонированием.

Направление ( ,β ) является самосопряженным,т.е.сопряжено само с собой, тогда и только тогда,когда

a11 2 + 2a12 β + a22β2 = 0,

т.е.оно является асимптотическим направлением.

Определение. Направление ( ,β ) называется особым,если оно сопряжено с каждым направлением ( , β ).

Теорема45.2. Любая параболическая кривая имеет единственное особое направление,которое совпадает с ее асимптотическим направлением.

Доказательство. Направление ( ,β ) является особым тогда и только тогда,когда

a11 + a12β = 0, a12 + a22β = 0.

Эта система линейных уравнений имеет ненулевое решение в том и только в том случае,когда ее определитель равен нулю,т.е.

"	a11	a12	"
"	a12	a22	"	= δ = 0.
"			"
"			"

В этом случае коэффициенты уравнений пропорциональны,и уравнения имеют единственное(с точностью до пропорциональности)решение ( ,β ) = (−a12, a11). Однако это и есть асимптотическое направление параболической линии.

Следствие45.2. Особое направление параболической кривой определяется собственным вектором матрицы Q,соответствующим собственному числу 0.

Лемма45.1. Пусть направление ( ,β ) не является особым.Тогда существует единственное сопряженное ему направление ( , β ).

Доказательство. Направление ( , β ),сопряженное направлению ( ,β ),находится из уравнения

(a11 + a12β) + β (a12 + a22β) = 0.

Поскольку направление ( ,β ) неособое,то по крайней мере одно из чисел a11 +a12β , a12 + a22β отлично от нуля.Тем самым,мы можем положить

( , β ) = (−(a12 + a22β), a11 + a12β).

Этот вектор единственен с точностью до умножения на ненулевое число.

Мы видели,что для параболических кривых особое направление,которое является асимптотическим,сопряжено любому направлению.Других случаев,когда оказываются сопряженными неасимптотическое и асимптотическое направления,быть не может.

Теорема45.3. Для центральной кривой (δ 6= 0) направление ( , β ),сопряженное неасимптотическому направлению ( ,β ),также является неасимптотическим.

84

Доказательство. Предположим,что направление ( , β ) асимптотическое.Тогда получаем систему из двух уравнений(первое условие сопряженности направлений ( ,β ) и ( , β ),а второе условие асимптотичности направления ( , β ):

(a11 + a12β) + β (a12 + a22β) = 0,(a11 + a12β ) + β (a12 + a22β ) = 0.

Рассмотрим эту систему как систему линейных уравнений относительно ( , β ). Она имеет ненулевое решение тогда и только тогда,когда ее определитель равен нулю:

"

a11 + a12β

a12 + a22β

" = 0.

a11

+ a12β

a12 + a22β

Разложим определитель

"

"

из определителей общие

"на сумму определителей и вынесем"

"

"

множители элементов столбцов:

a11a22

"

β

" − a122

"

β

" = δ

"

β

"

= 0.

β

β

β

"

"

"

"

"

"

"

"

"

"

"

"

"

"

"

"

"

"

Следовательно,либо δ = 0,либо векторы ( ,β ) и ( , β ) коллинеарны.Последнее невозможно,поскольку ( ,β ) неасимптотическое направление,а ( , β )асимптотическое.

Таким образом,асимптотическое направление может быть сопряженным неасимптотическому только в случае нецентральной кривой (δ = 0).

Определение. Диаметры кривой второго порядка называются сопряженными,если они имеют сопряженные направления.

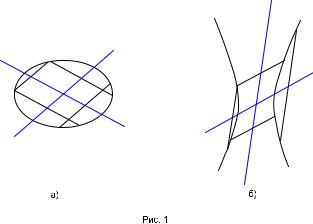
На рис. 1а)изображены сопряженные диаметры эллипса,на рис. 1б) гиперболы.

Каждый из сопряженных диаметров делит пополам хорды,параллельные второму диаметру.

Замечание. Сопряженным направлениям не всегда соответствуют сопряженные диаметры.Действительно,может просто не существовать хорд данного направления.

§46.Главные диаметры и направления

Здесь систему координат снова считаем прямоугольной. Диаметр,сопряженный неасимптотическому направлению ( ,β ),перпендику-

лярный этому направлению,является осью симметрии кривой.Действительно,он делит пополам хорды этого направления и им перпендикулярен.

85

Определение. Направление ( ,β ) называется главным по отношению к данной кривой второго порядка F ,если перпендикулярное к нему направление с ним сопряжено.

Таким образом,любое особое направление является главным.Главным будет и направление,перпендикулярное особому.

Теорема46.1. Вектор ( ,β ) задает главное направление кривой

F = a11x2 + 2a12xy + a22y2 + 2a1x + 2a2y + a0 = 0

тогда и только тогда,когда он является собственным вектором матрицы Q,принадлежащий некоторому собственному числу λ.

Доказательство. Рассмотрим сначала неособое направление ( ,β ).Тогда с ним сопряжено(см.лемму45.1)единственное направление

( , β ) = (−(a12 + a22β), a11 + a12β).

Направления ( ,β ) и ( , β ) перпендикулярны тогда и только тогда,когда

+ ββ = 0,

а значит,неособое направление ( ,β ) является главным тогда и только тогда,когда векторы ( ,β ) и (β , − ) коллинеарны,т.е.

a11	+ a12β	= λ
a12	+ a22β		β		(46.1)

для некоторого λ.Для особого направления это равенство тоже выполняется(при этом λ = 0).

Тем самым,направление ( ,β ) является главным тогда и только тогда,когда

для него выполняется равенство(46.1),или			β .
Q β	= λ
Перепишем:		=	0 .
(Q − λE) β
			0

Эта система имеет ненулевое решение ( ,β ).Для этого определитель ее должен равняться нулю: det(Q − λE) = χQ(λ) = λ2 − Sλ + δ = 0.Рассмотрим его корень λ. Если λ = 0,то система перепишется в виде

a11 + a12β = 0, a12 + a22β = 0,

Умножим первое уравнение на ,второе на β ,и сложим полученные равенства:

a11 2 + a12 β + a22β2 = 0,

то есть ( ,β ) асимптотическое направление.

Если же λ 6= 0, то

a11 + a12β = λ , a12 + a22β = λβ,

86

Умножим первое уравнение на ,второе на β ,и сложим полученные равенства:

a11 2 + a12 β + a22β2 = λ( 2 + β2) 6= 0.

Таким образом,направление,определяемое собственным вектором матрицы Q,является главным.В случае λ 6= 0 это направление неасимптотическое,а следовательно, главное,так как условие коллинеарности и нормали к сопряженному диаметру,как мы показали,эквивалентно условию

(Q − λE)	β	=	0 .
			0

В случае λ = 0 оно асимптотическое и особое,следовательно,оно также является главным.

Следствие46.1. Каждая кривая второго порядка,оличная от окружности,имеет ровно два различных главных направления.Для окружности(возможно,мнимой или нулевого радиуса)все направления являются главными.

Доказательство. По лемме36.2матрица Q всегда имеет два собственных вектора.

Поскольку направление,перпендикулярное главному,очевидно,также является главным,то найденные главные направления взаимно перпендикулярны.

Определение. Диаметр кривой второго порядка называется главным,если он сопряжен перпендикулярному ему направлению,т.е.если он перпендикулярен некоторому главному направлению.

Любой главный диаметр является осью симметрии кривой.Обратное,вообще говоря,неверно(например,рассмотрим перпендикулярные прямые).

Направление главного диаметра является главным направлением.Обратное тоже неверно(например,для параболических линий все диаметры имеют асимптотическое направление,но существует главное направление,перпендикулярное асимптотическому направлению,которое неасимптотическое и не является направлением главного диаметра).

Таким образом,для параболических кривых существует только один главный диаметр.Для центральных кривых,отличных от окружности,существует два взаимно перпендикулярных главных диаметра.Для окружности все диаметры являются главными.

Итак,каноническая система координат имеет следующий вид:

Осью абсцисс этой системы является главный диаметр(единственный для нецентральных кривых и любой из двух главных диаметров для центральных кривых).

Осью ординат этой системы является второй главный диаметр для центральных кривых и прямая,перпендикулярная главному диаметру для нецентральных кривых (в случае параболы эта прямая проходит через точку пересечения кривой с главным диаметром).

87

ЛЕКЦИЯ14.КАСАТЕЛЬНАЯ.АФФИННЫЕ ПРЕОБРАЗОВАНИЯ

§47.Касательная к кривой второго порядка

Определение. Особой точкой кривой второго порядка называется центр,принадлежащий кривой.

Так,особыми точками являются точка пересечения пары пересекающихся прямых,все точки пары совпадающих прямых и единственная точка пары мнимых пересекающихся прямых.

Все особые точки удовлетворяют условиям

F (x0, y0) =	@F	(x0, y0) =	@F	(x0, y0) = 0.
	@x		@y

Определение. Касательной к кривой второго порядка F в неособой точке (x0, y0) называется прямая,проходящая через эту точку и пересекающая F в двух совпавших точках,либо содержащаяся в F .

Теорема47.1. Касательная к кривой

F (x, y) = a11x2 + 2a12xy + a22y2 + 2a1x + 2a2y + a0 = 0

в неособой точке (x0, y0) имеет уравнение

@F

@F

(x0, y0)(x − x0) +

(x0, y0)(y − y0) = 0,

@x

@y

или

(a11x0 + a12y0 + a1)x + (a12x0 + a22y0 + a2)y + (a1x0 + a2y0 + a0) = 0.

(47.1)

Доказательство. Прямая

x = x0 + t, y = y0 + βt

пересекает кривую в точках,соответствующим решениям уравнения

F2t2 + 2F1t + F0 = 0,

где

F2 = a11 2 + 2a12 β + a22β2 = q( ,β ),

F1 = (a11x0 + a12y0 + a1) + β(a12x0 + a22y0 + a2) =

1

@F

1

@F

=

(x0, y0) +

β

(x0, y0),

2

@x

2

@y

F0 = F (x0, y0) = 0,

поскольку точка лежит на кривой.Условие касания F1 = 0,то есть

@F

@F

(x0, y0) + β

(x0, y0) = 0,

@x

@y

88

следовательно,можно взять ( ,β ) так,чтобы
= −	@F	(x0, y0), β =	@F	(x0, y0).
	@y		@x

Поскольку точка (x0, y0) неособая,то этот вектор ненулевой.Так как при сколь угодно малом возмущении(повороте)будет уже F1 6= 0,то есть секущая,то это две совпавшие точки.Получаем

@F	(x0, y0)(x − x0) +	@F	(x0, y0)(y − y0) = 0
@x		@y

или

(a11x0 + a12y0 + a1)(x − x0) + (a12x0 + a22y0 + a2)(y − y0) = 0.

С учетом F (x0, y0) = 0 это дает

(a11x0 + a12y0 + a1)x + (a12x0 + a22y0 + a2)y + (a1x0 + a2y0 + a0) = 0.

§48.Оптические свойства эллипса,гиперболы и параболы

Эллипс,гипербола и парабола в каждой своей точке имеют касательные,поскольку их центры симметрии(в случае эллипса и гиперболы)не лежат на самих кривых или(в случае параболы)центра симметрии просто нет.

Далее будем считать,что луч отражается от кривой как от ее касательной. Решим сначала вспомогательную задачу.

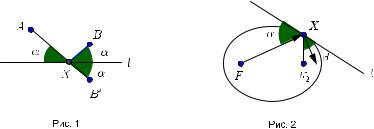
Задача1. Для данной прямой l и двух точек A и B ,лежащих по одну сторону от нее,найти такую точку X 2 l,что сумма расстояний |XA| + |XB| минимальна.

Решение. Построим точку B0 ,симметричную B относительно l (рис. 1). Ясно,что сумма |AX| + |XB0| минимальн при X = (AB0) \ l.Но |XB| = |XB0|,

так что минимум достигается при равенстве острых углов,образуемых AX и BX с l.

Теорема48.1. Лучи света,исходящие из одного фокуса эллипса,после зеркального отражения от эллипса проходят через его второй фокус.

Доказательство. Из геометрического определения эллипса следует,что сумма расстояний от любой точки,находящейся внутри эллипса,до его фокусов,меньше 2a, а сумма расстояний от любой точки,находящейся снаружи эллипса,до его фокусов, больше 2a.

Пусть луч света вышел из фокуса F1 и,отразившись от точки X эллипса,не попал в другой фокус F2 (рис. 2).Значит,если l касательная в точке X ,то углыи β не равны,а сумма расстояний |F1X|+|F2X| не минимальна при пробегании X по l.Но все остальные точки касательной лежат вне эллипса,следовательно,сумма расстояний от любой из них до фокусов больше |F1X| + |F2X|.

89

Для доказательства оптического свойства гиперболы понадобится еще одна вспомогательная задача.

Задача2. Для данной прямой l и двух точек A и B ,лежащих по разные стороны от нее,найти такую точку X 2 l,что модуль разности расстояний от нее до точек A и B ||AX| − |BX|| максммален.

Решение. Построим точку B0 ,симметричную B относительно l (рис. 3). Ясно,что ||AX| − |XB0|| максимален при X = (AB0) \ l.Но |XB| = |XB0|,так

что максимум достигается при равенстве острых углов,образуемых AX и BX с l. С помощью этой задачи доказывается оптическое свойство гиперболы.

Теорема48.2. Лучи,исходящие из одного фокуса гиперболы,после зеркального отражения от гиперболы кажутся исходящими из другого ее фокуса.

А теперь докажем оптическое свойство параболы.

Теорема48.3. Лучи,исходящие из фокуса параболы,после зеркального отражения от параболы,становятся параллельными оси параболы.

Доказательство. Рассмотрим параболу с фокусом F и директрисой d.Пусть луч вышел из фокуса F и отразился от точки X параболы.Пусть Y проекция точки X на d.Пусть l серединный перпендикуляр к Y F .По определению параболы,

треугольник XY F равнобедренный,и				l проходит через X .Докажем,что				l является
касательной к параболе в точке X .Предположим противное.Тогда имеется еще
одна точка пересечения			с параболой	6	, а	Y 0	ее проекция на директрису
		l		X0 = X
d (рис.	4).Тогда по свойству серединного перпендикуляра |Y X0| = |X0F |, а так
как X0	точка параболы,то |Y 0X0|			= |X0F |.Значит, |X0Y 0| = |X0Y |,но длина
наклонной должна быть больше длины перпендикуляра.Таким образом,								l является

касательной.

При этом углы между Y X и l и между F X и l равны,так что отраженный луч лежит на продолжении Y X?d.

90