geometry24

Определение. Линия на поверхности называется линией кривизны,если ее направление в каждой точке является главным направлением.

Если координатные линии на поверхности являются линиями кривизны,то коэффициенты F первой квадратичной формы и M второй квадратичной формы равны нулю. F = 0 в силу ортогональности координатной сети,а M = 0 в силу сопряженности.

§110.Связь между главными кривизнами и нормальной кривизной

Выразим нормальную кривизну поверхности в произвольном направлении через нормальные кривизны.Введем прямоугольную систему координат Oxyz,приняв касательную плоскость поверхности в произвольной точке O за плоскость xy, а нормаль поверхности за ось z.Выберем оси x и y так,чтобы они совпадали с главными направлениями в точке O.

Пусть z = z(x, y) уравнение поверхности в окрестности точки O при таком выборе системы координат.В точке O zx = 0, zy = 0.Поэтому в точке O

I = dx2 + dy2,

II = rdx2 + 2sdxdy + tdy2.

Так как направления (0 : dy) и (δx : 0) в точке O главные направления,сопряжены,то s = 0 и,следовательно,

II = rdx2 + tdy2.

Отсюда нормальная кривизна в произвольном направлении (dx : dy)

rdx2 + tdy2 k = dx2 + dy2 .

Взяв направления (0 : dy) и (δx : 0),видим,что r и t являются главными кривизнами.

Пусть угол,образуемый произвольным направлением (dx : dy) с главным направлением (δx : 0), k нормальная кривизна в этом направлении, k1 и k2 главные кривизны,соответствующие направлениям (δx : 0) и (0 : dy) соответственно.Тогда из выражения нормальной кривизны получается формула Эйлера для нор-

мальной кривизны в произвольном направлении

k = k1 cos2 + k2 sin2 .

Для получения нормальной кривизны в произвольном направлении достаточно знать главные кривизны.

Найдем выражения для главных кривизн в случае произвольного задания поверхности.

Пусть k1 и k2 главные кривизны поверхности и пусть для определенности k1 ≥ k2 .В этом случае k1 является максимумом,а k2 минимумом отношения квадратичных форм

II L 2 + 2M + N 2

I = E 2 + 2F + G 2 .

Пусать ¯ значения переменных ,при котором это отношение достигает мак-

, ¯ ,

симума(существование таких , нам уже известно).Тогда для всех , II − k1I 0,

211

причем для ¯

= ,

ний то есть

= ¯ достигается равенство.Отсюда следует,что для этих значе-

(II − k1I)0 = 0, (II − k1I)0 = 0,

¯	¯
L + M ¯ − k1	(E + F ¯) = 0,
¯	¯

M + N ¯ − k1(F + G¯) = 0.

¯	и ¯,получим уравнение для k1 :
Исключая из этих равенств
"	−	−	"
"	L k E M	k1F	"
"	M− k11F N	−k1G	"	= 0.
"			"

Таким образом,получено уравнение для главных кривизн.Разложив его на сумму определителей,его можно записать в другом виде:

k2(EG − F 2) − k(LG − 2MF + NE) + (LN − M2) = 0.

212

ЛЕКЦИЯ33.НЕКОТОРЫЕ ТИПЫ ПОВЕРХНОСТЕЙ

§111.Средняя и гауссова кривизны

Определение. Полусумма главных кривизн поверхности называется средней кривизной поверхности:

H = k1 + k2 .

2

Если k и k + /2 нормальные кривизны поверхности в двух взаимно перпендикулярных направлениях,то их полусумма равна средней кривизне поверхности.

Действительно,по формуле Эйлера имеем

k = k1 cos2 + k2 sin2 ,

k + /2 = k1 cos2( + /2) + k2 sin2( + /2) = k1 sin2 + k2 cos2 .

Складываем полученные значения:

k + k + /2 = k1 cos2 + k2 sin2 + k1 sin2 + k2 cos2 = k1 + k2,

откуда и получаем требуемое.

Среднее значение нормальных кривизн поверхности в данной точке

1 Z 2

2 0

k d

равно средней кривизне поверхности в этой точке.И это свойство также получается сразу из формулы Эйлера:

1			Z0			2
								k
	2					Z0
		1						2
=
		2						Z0
= k1					1
				2

				1	2
d =					Z0	(k1 cos2 + k2 sin2 )d =
			2
	1 + cos 2											cos 2
k1							+ k2	1		−				d =
					2							2
2	1 +			cos 2						1		2 1		cos 2		k	1	+ k	2
						d + k2						Z0		− 2	d =					.
				2					2									2

Определение. Произведение главных кривизн поверхности называется гауссовой или полной кривизной поверхности:

K = k1k2.

Средняя и гауссова кривизны поверхности легко выражаются через коэффициенты первой и второй квадратичных форм из квадратного уравнения для главных кривизн по формулам Виета:

H =	1	LG − 2MF + NE	, K =	LN − M2	.
	2 EG − F 2			EG − F 2

Знак гауссовой кривизны определяется знаком LN −M2 .Поэтому гауссова кривизна положительна в эллиптических точках,отрицательна в гиперболических и равна нулю в параболических точках и точках уплощения.

213

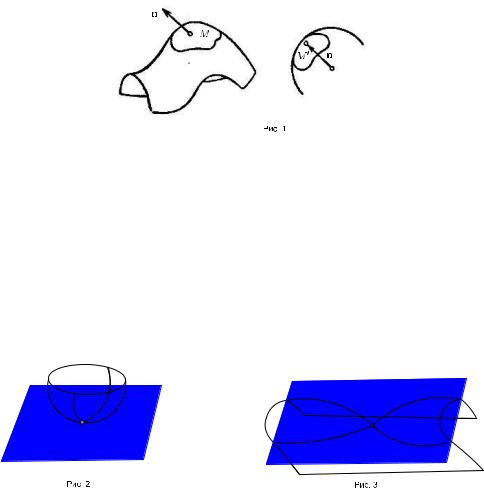
Пусть M произвольное множество точек на поверхности.Отложим от произвольной точки O единичные векторы нормалей к поверхности точек множества M .Концы этих нормалей образуют некоторое множество M0 на единичной сфере(рис. 1).Это множество называется сферическим изображением множества M .

Теорема111.1. (Гаусс)Отношение площади сферического изображения области на поверхности к площади этой области стремится к абсолютному значению гауссовой кривизны в данной точке O поверхности,когда область стягивается к этой точке.

§112.Геометрический смысл второй квадратичной формы поверхности

С помощью второй квадратичной формы поверхности производится изучение пространственного строения окрестности точки на поверхности.Обозначим

2h = Ldu2 + 2Mdudv + Ndv2.

Величина h с точностью до малых более высокого порядка относительно du, dv равна расстоянию от точки M0 поверхности с координатами (u + du, v + dv) до касательной плоскости в точке M с координатами (u, v),причем расстояние берется со знаком,в зависимости от того,с какой стороны от расположена точка M .Это сразу получается,если уравнение поверхности записать в системе координат с началом в точке M ,в которой касательная плоскость к поверхности в точке M является плоскостью xy,а нормаль осью z.Если вторая квадратичная форма знакоопределенная,то поверхность в достаточно малой окрестности этой точки располагается по одну сторону от касательной плоскости в данной точке,и в этом случае точка M эллиптическая(рис. 2).

Если вторая квадратичная форма знакопеременная,то поверхность в окрестности точки M располагается по разные стороны от плоскости ,и точка M гиперболическая(рис. 3).

Если вторая квадратичная форма знакоопределенная,но принимает нулевые значения при не равных нулю одновременно du и dv,то точка M параболическая(рис. 4).

§113.Линейчатые поверхности

214

Определение. Линейчатой поверхностью называется поверхность,описанная движением прямой,называемой образующей,пересекающей при движении некоторую кривую γ ,называемую направляющей поверхности.

Пусть уравнение направляющей кривой γ имеет вид % = %(u), u 2 ( ,β ), а единичный вектор образующей d в точке,соответствующей значению параметра u, есть µ(u) (рис. 5).

Уравнение линейчатой поверхности S ,образованной движением образующей d, пересекающей направляющую γ ,имеет вид

r(u, v) = %(u) + vµ(u), u 2 ( ,β ), v 2 R,

где r(u, v) радиус-вектор произвольной точки P (u, v) на поверхности S . Поскольку ru = %0u + vµ0u , rv = µ(u),то нормальный вектор линейчатой поверх-

ности имеет вид

n = [ru, rv] = [%0u, µ] + v[µ0u, µ].

Первая квадратичная форма линейчатой поверхности с учетом µ2 = 1, (µ0u, µ) = 0 имеет вид

I = dr2 = ((%0u + µ0uv)du + µ(u)dv)2 =

= (%0u2 + 2(%0u, µ0u)v + µ0u2v2)du2 + 2(µ,% 0u)dudv + dv2.

Определение. Линейчатая поверхность называется развертывающейся,если ее касательная плоскость остается неизменной вдоль прямолинейной образующей,в противном случае линейчатую поверхность называют косой поверхностью.

Рассмотрим три примера,исчерпывающие класс развертывающихся линейчатых поверхностей.

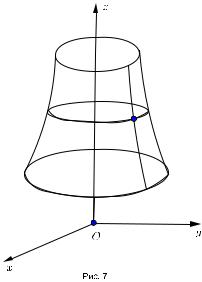
Коническая поверхность с вершиной в точке M(%0) и направляющей % = %(u) имеет уравнение

r(u, v) = %0 + vµ(u),

где µ единичный вектор,коллинеарный % − %0 ,и тем самым,является линейчатой поверхностью(рис. 6).На-

правление нормального вектора,вычисленного в произ- вольной точке образующей,остается неизменным,так как

n(u, v) = [µ0u, µ]v.

Таким образом,коническая поверхность есть развертывающаяся поверхность,и ее первая квадратичная форма имеет вид

215

I = dr2 = µ0u2v2du2 + dv2.

Цилиндрическая поверхность с направляющей % = %(u) и образующей с постоянным единичным направляющим вектором µ имеет уравнение

r(u, v) = %(u) + vµ,

и для нее нормальный вектор n(u, v) = [%0u, µ] остается неизменным вдоль образующей,т.е.всякая цилиндрическая поверхность является развертывающейся,а ее первая квадратичная форма

I = %0u2du2 + 2(%0u, µ)dudv + dv2.

Поверхность,образованная касательными к некоторой кривой % = %(u) также является развертывающейся поверхностью.Действительно,для указанной поверхности направляющий вектор образующей µ(u) = %0(u),а поэтому нормальный вектор касательной плоскости в произвольной точке образующей совпадает с вектором [%00uu, %0u]v и не меняет своего направления.

Следовательно,поверхность касательных является развертывающейся поверхностью,а ее первая квадратичная форма имеет вид

I = (%0u + v%00uu)2du2 + 2(%0u2 + v(%00uu, %0u))dudv + %0u2dv2.

Развертывающиеся поверхности характеризуются тем,что касательная плоскость к ним в различных точках одной и той же образующей неизменна.Совокупность всех касательных плоскостей развертывающейся линейчатой поверхности представляет собой однопараметрическое семейство.Иначе говоря,развертывающаяся линейчатая поверхность является огибающей однопараметрического семейства плоскостей.

§114.Поверхности вращения

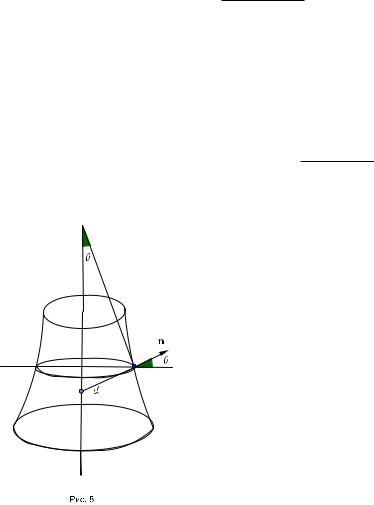
Определение. Поверхность F называется поверхностью вращения,если она образуется вращением некоторой кривой вокруг оси.Линии пересечения поверхности с плоскостями,проходящими через ось вращения,называются меридианами,а линии пересечения с плоскостями,перпендикулярными оси,называются

параллелями (рис. 7).

Составим уравнение поверхности вращения,которая образуется при вращении кривой γ

x = x(u), z = z(u), (x ≥ 0)

расположенной в плоскости xz,вокруг оси z.Точка (x(u), 0, z(u)) кривой γ при повороте кривой на угол v переходит в точку

(x(u) cos v, x(u) sin v, z(u)).

216

Отсюда уравнение поверхности вращения

x = x(u) cos v, y = x(u) sin v, z = z(u).

Линии u = const являются меридианами,а v = const параллелями.Найдем первую квадратичную форму поверхности:

ru = (x0(u) cos v, x0(u) sin v, z0(u)), rv = (−x(u) sin v, x(u) cos v, 0), E = (ru, ru) = x02 + z02, F = 0, G = x2,

откуда

I = (x02 + z02)du2 + x2dv2.

Меридианы и параллели поверхности образуют ортогональную сеть,поскольку F = 0.Геометрически это очевидно.

Найдем вторую квадратичную форму поверхности:

ruu = (x00(u) cos v, x00(u) sin v, z00(u)), ruv = (−x0(u) sin v, x0(u) cos v, 0),

rvv = (−x(u) cos v, −x(u) sin v, 0),

p

= p

= p

= xp

.

откуда

EG − F 2

EG

(x02 + z02)x2

x02 + z02

"

x00 cos v

x00 sin v

z00

"

"

−x0 sin v

x0 cos v

0

"

x0 cos v

x0 sin v

z0

x0 cos v

x0 sin v

z0

"

"

z00x0

z0x00

"

"

"

x sin v

x cos v

0

"

"

x sin v

x cos v

0

"

"

−

"

"

"

L =

"

"

=

−

, M =

"

−

"

= 0,

"

"

(x0

2

+ z0

2

)x

2

(x0

2

2

)

(x0

2

+ z0

2

)x

2

−

+ z0

"

"

p

v

−

p

"

x cosp

x sin v

0

"

x0 cos v

x0 sin v

z0

"

"

xz0

"

x sin v

x cos v

0

"

"

"

N =

"

−

"

=

.

"

"

x0

2

+ z0

2

(x0

2

+ z0

2

)x

2

p Отсюда

z00

x0 − z0x00

z0x

II =

du2 +

dv2.

px02 + z02

px02 + z02

Параллели и меридианы образуют сопряженную сеть

(M = 0).Значит,параллели и меридианы являются

линиями кривизны.

Коэффициенты I и II зависят только от u.

Найдем главные кривизны поверхности враще-

ния.Пусть k1

кривизна меридиана, k2 кривиз-

на параллели, угол,образованный касательной

меридиана с осью поверхности.Так как плоскость

меридиана содержит нормаль к поверхности,то нор-

мальная кривизна поверхности в направлении мери-

диана равна кривизне меридиана,т.е.

k1 .Для кри-

визны поверхности в направлении параллели по тео-

реме Мёнье получаем значение k2 cos (радиус кри-

визны окружности,которая является параллелью,

равен ее радиусу).Величина

k2 cos имеет простой

геометрический смысл.Именно,если обозначить d

длину отрезка нормали поверхности до точки пере-

сечения с осью,то

k2 cos = 1/d.

217

ЛИТЕРАТУРА

1.Александров П.С. “Лекции по аналитической геометрии”,М.: “Наука”, 1968, 912с.

2.Балк М.Б.,Болтянский В.Г. “Геометрия масс”,М.: “Наука”, 1987, 160с.

3.Беклемишев Д.В. “Курс аналитической геометрии и линейной алгебры”,М.: “Высшая школа”, 1998, 320с.

4.Беклемишева Л.А.,Петрович А.Ю.,Чубаров И.А. “Сборник задач по анали-

тической геометрии и линейной алгебре”,М.:Физматлит, 2001, 496с.

5.Н.В.Ефимов Н.В. “Высшая геометрия”,М.: “Наука”, 1971, 576с.

6.Иванова Е.Е. “Дифференциальное исчисление функций одного переменного”, Изд-во МГТУ им.Баумана, 1998, 407с.

7.Ильин В.А.,Позняк Э.Г. “Аналитическая геометрия”,М.: “Наука”, 1999, 224с.

8.Клейн Ф. “Неевклидова геометрия”,М.-Л.:ОНТИ НКТП СССР, 1936, 356с.

9.Кудрявцев Л.Д. “Курс математического анализа”.Т.1.Дифференциальное и интегральное исчисления функций одной переменной,Дрофа, 2008, 704с.

10.Кузютин В.Ф.,Зенкевич Н.А.,Еремеев В.В. “Геометрия”,Лань, 2003, 416с.

11.Моденов П.С.,Пархоменко А.С. “Сборник задач по аналитической геометрии”,

М.: “Наука”, 1976, 384с.

12.Мусхелишвили Н.И. “Курс аналитической геометрии”,М.: “Высшая школа”, 1967, 655с.

13.Постников М.М. “Аналитическая геометрия”,М.: “Наука”, 1973, 754с.

14.Прасолов В.В.,Тихомиров В.М. “Геометрия”,М.:Изд-во МЦНМО, 2007, 328с.

15.Погорелов А.В. “Дифференциальная геометрия”,М.: “Наука”, 1974, 176с.

16.Рашевский П.К. “Курс дифференциальной геометрии”,Л.:ГИТТЛ, 1950, 428 с.

17.Троицкий Е.В. “Аналитическая геометрия”,Изд-во МГУ, 2003, 118с.

18.Чернавский А.В. “Лекции по дифференциальной геометрии.ЧастьIII.Кривые и поверхности”, http://higeom.math.msu.su/people/chernavski/chern3.pdf

19.Энциклопедия элементарной математики.Т. 5.Геометрия.М.: “Наука”, 1966, 624с.

218

ОГЛАВЛЕНИЕ
Лекция1.Некоторые сведения из алгебры . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1
§ 1.Определители второго порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1
§ 2.Определители третьего порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	3
§ 3.Основные свойства определителей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	3
§ 4.Система трех линейных уравнений с тремя неизвестными с определителем,
отличным от нуля. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	6
§ 5.Понятие определителя любого порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	7
Лекция2.Векторы в пространстве . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	9
§ 6.Векторы и линейные операции над ними . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	9
§ 7.Линейная зависимость и независимость векторов.Базис . . . . . . . . . . . . . . . . . . . .	13
Лекция3.Центр масс.Скалярное произведение . . . . . . . . . . . . . . . . . . . . . . . . . .	17
§ 8.Деление отрезка в данном отношении . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	17
§ 9.Барицентрические координаты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	18
§10.Скалярное произведение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	19
Лекция4.Площадь,объем и ориентация . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	22
§11.Ориентированная площадь . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	22
§12.Ориентированный объем . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	23
§13.Векторное и смешанное произведения векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	24
§14.Двойное векторное произведение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	26
Лекция5.Замены координат.Системы координат . . . . . . . . . . . . . . . . . . . . . . .	28
§15.Замены координат . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	28
§16.Прямоугольные системы координат и ортогональные матрицы . . . . . . . . . . . . .	30
§17.Углы Эйлера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	32
§18.Полярные,сферические и цилиндрические координаты . . . . . . . . . . . . . . . . . . . .	34
Лекция6.Прямые на плоскости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	36
§19.Алгебраические кривые . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	36
§20.Различные виды уравнений прямой на плоскости . . . . . . . . . . . . . . . . . . . . . . . . . . .	37
§21.Взаимное расположение двух прямых на плоскости . . . . . . . . . . . . . . . . . . . . . . . .	40
Лекция7.Прямые и плоскости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	42
§22.Пучки прямых на плоскости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	42
§23.Прямая на плоскости в прямоугольной системе координат . . . . . . . . . . . . . . . . .	43
§24.Различные виды уравнений плоскости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	44
Лекция8.Плоскости и прямые в пространстве . . . . . . . . . . . . . . . . . . . . . . . . . . .	48
§25.Взаимное расположение плоскостей в пространстве . . . . . . . . . . . . . . . . . . . . . . . .	48
§26.Пучки и связки плоскостей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	48
§27.Плоскость в прямоугольной системе координат . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	49
§28.Прямая в пространстве . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	50
§29.Некоторые формулы в прямоугольной системе координат . . . . . . . . . . . . . . . . . .	51
Лекция9.Эллипс,гипербола,парабола . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	54
§30.Геометрические определения эллипса,гиперболы и параболы . . . . . . . . . . . . . .	54
§31.Эллипс,гипербола и парабола как конические сечения . . . . . . . . . . . . . . . . . . . . .	54

219

§32.Аналитическое определение коник . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	57
Лекция10.Полярные уравнения коник.Общая теория . . . . . . . . . . . . . . . . . .	61
§33.Фокальный параметр . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	61
§34.Полярные уравнения коник . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	61
§35.Параметрические уравнения коник . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	62
§36.Общая теория кривых второго порядка.Канонические уравнения . . . . . . . . . .	63
Лекция11.Определение вида и расположения кривых . . . . . . . . . . . . . . . . . .	69
§37.Примеры . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	69
§38.Инварианты многочлена второй степени . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	72
§39.Полуинвариант . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	73
Лекция12.Вид кривой и инварианты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	75
§40.Определение канонического уравнения по инвариантам . . . . . . . . . . . . . . . . . . . .	75
§41.Распадающиеся кривые . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	77
§42.Центры кривых второго порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	77
§43.Асимптотические направления кривых второго порядка . . . . . . . . . . . . . . . . . . . .	80
Лекция13.Диаметры кривой второго порядка . . . . . . . . . . . . . . . . . . . . . . . . . . .	82
§44.Диаметры . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	82
§45.Сопряженные диаметры и направления . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	83
§46.Главные диаметры и направления . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	85
Лекция14.Касательная.Аффинные преобразования . . . . . . . . . . . . . . . . . . . .	88
§47.Касательная к кривой второго порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	88
§48.Оптические свойства эллипса,гиперболы и параболы . . . . . . . . . . . . . . . . . . . . . .	89
§49.Аффинные преобразования . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	91
Лекция15.Движения и подобие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	95
§50.Движения и изометрические преобразования . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	95
§51.Движения плоскости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	95
§52.Движения пространства . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	97
§53.Подобие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	99
Лекция16.Поверхности второго порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	101
§54.Поверхности второго порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	101
Лекция17.Основные виды поверхностей второго порядка . . . . . . . . . . . . . .	107
§55.Эллипсоид . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	107
§56.Однополостный гиперболоид . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	107
§57.Двуполостный гиперболоид . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	110
§58.Конус второго порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	110
§59.Эллиптический параболоид . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	111
§60.Гиперболический параболоид . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	112
§61.Нераспадающиеся цилиндры . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	113
Лекция18.Общая теория поверхностей второго порядка . . . . . . . . . . . . . . .	115
§62.Центры поверхностей второго порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	115
§63.Пересечение поверхности второго порядка с прямой . . . . . . . . . . . . . . . . . . . . . . . .	116
§64.Определение вида и расположения поверхности второго порядка . . . . . . . . . . .	118
Лекция19.Элементы проективной геометрии . . . . . . . . . . . . . . . . . . . . . . . . . . .	121

220