geometry24

Тем самым,геометрически центр кривизны это центр соприкасающейся окружности кривой.Поэтому эволюта геометрическое место центров кривизны плоской кривой.

Замечание1. Расстояние между соответствующими точками эволюты и данной кривой равно радиусу кривизны,так как % = |R − r(s)| = |p(s)n(s)| = p(s).

Замечание2. Точки эволюты лежат на нормали кривой со стороны ее вогнутости,так как p(s) > 0.

Пусть γ регулярная кривая,для которой всюду k0(s) сохраняет знак и k(s) нигде не обращается в нуль.В этом случае эволюта $ кривой γ является регулярной

кривой без особых точек.

Найдем длину отрезка эволюты,соответствующего отрезку

s1s2 кривой.Имеем

n

tk

1

0

1

0

R0

= r +

0

= t +

−

+ n

= n

,

k

k

k

k

Z

Z

"

1

0

"

S(s1, s2) =

s2

|R0|ds =

s2

"

" ds.

s1

s1

k

"

"

Отсюда,так как k0

сохраняет знак,получаем

"

"

"

"

1

1

"

"

S(s1, s2) = "

k(s2)

−

k(s1)

" .

"

"

Таким образом,длина дуги отрезка эволюты равна абсолютной величине разности радиусов кривизны кривой в точках,соответствующих концам этого отрезка.

181

ЛЕКЦИЯ28.ЭВОЛЬВЕНТА.ПОВЕРХНОСТЬ

§94.Эвольвента плоской кривой

Определение. Эвольвентой кривой γ называется такая кривая $,по отношению к которой γ является эволютой.

Пусть r = r(s) естественная параметризация кривой γ .Будем обозначать через t и n единичные векторы касательной и главной нормали этой кривой.Радиусвектор точки эвольвенты R(s) очевидно допускает представление

R(s) = r(s) + λ(s)t(s).

Дифференцируя это равенство по s,получим

R0(s) = t + λ0t + λkn.

Отсюда,так как R0 перпендикулярен t, λ0 = −1.Следовательно, λ = c − s. Таким образом,если кривая имеет эвольвенту,то она задается уравнением

R = r(s) + t(c − s),

где c = const.

Убедимся,что каждая кривая,задаваемая этим уравнением,имеет своей эволютой кривую γ и,следовательно,является для нее эвольвентой.

Найдем кривизну K кривой $ (кривизну γ будем обозначать через k):

R0 = r0(s) + t0(c − s) − t = t0(c − s) = kn(c − s),

R00 = k0n(c − s) + k(−kt)(c − s) − kn = (k0(c − s) − k)n − k2(c − s)t,

	K2 =	[R0, R00]2	=	k6(c − s)4[n, −t]2	=		1	, K =	1	,
		(R02)3				(c − s)2			c − s
				(k2(c − s)2)3

поскольку рассматриваем значения параметра s < c.

Как видно из выражения для R0 ,касательным вектором кривой $ является вектор n единичный вектор нормали к кривой γ .Следовательно,единичный вектор нормали будет направлен перпендикулярно вектору n,т.е.он будет или совпадать

с вектором, t,или совпадать с вектором

−t.Вектор

R00 направлен в сторону во-

гнутости кривой(он показывает направление изменения вектора R0 .Нас интересует

его

составляющая,ортогональная касательной,т.е.

−

k2(c

−

s)t.Поскольку в нашем

2

случае k

> 0,то единичный вектор нормали совпадает с вектором −t.

Уравнение эвольвенты кривой γ в случае произвольной параметризации,оче-

видно

R = r(t) − prr0(02t(t) Z pr02(t)dt,

или,в скалярной форме

)

Z p

x0(t)

dt,

X = x(t) −

x02(t) + y02(t)

p

x0(t) + y02(t)

182

		y0(t)		Z p		dt.
Y = y(t) −					x02(t) + y02(t)
	p

x0(t) + y02(t)

Вуравнении эвольвенты присутствует произвольная постоянная c.Тем самым,

укривой γ имеется бесконечно много эвольвент.Рассмотрим две эвольвенты

R1 = r(s) + (−s + c1)t(s) и R1 = r(s) + (−s + c1)t(s).

Найдем расстояние между соответствующими точками эвольвент:

% = |R1(s) − R2(s)| = |(c1 − c2)t| = |c1 − c2|.

Тем самым,это расстояние постоянно.

Наглядно образование эвольвенты можно представить следующим образом. Представим нерастяжимую нить,натянутую на часть кривой γ ,соответствующую s < c,с концом в точке Q(c).Если натягивать нить и одновременно отделять ее от кривой так,чтобы нить была направлена по касательной,то ее свободный конец опишет эвольвенту.

Эвольвентой окружности является спиралевидная кривая.Её уравнения имеют следующий вид:

x = r(cos ' + (' − c) sin '), y = r(sin ' − (' − c) cos ').

где ' угол, a r радиус(на рис. 1приведена эвольвента окружности единичного радиуса при c = 0).

В технике эвольвенту окружности используют как профиль зуба для колес зубчатой передачи(рис. 2).Эвольвентное зацепление предложил Л.Эйлер.

Пусть боковые поверхности зубьев двух цилиндрических зубчатых колёс с параллельными осями вращения,проходящими через точки O1 и O2 (рис. 3),очерчены по эвольвентам,а линия контакта зубьев при некотором расположении колес проходит через точку K .Тогда в точке K нормали KM1 и KM2 к эвольвентам $1 и $2 будут лежать на отрезке M1M2 общей касательной к окружностям радиусов r1 и r2 соответственно(эти окружности по отношению к эвольвентам являются эволютами).При вращении колес точка K перемещается вдоль отрезка M1M2 (новое положение эвольвент показано на рисунке штриховыми линиями)до тех пор,пока рассматриваемая пара зубьев не выйдет из взаимного зацепления.Однако зубчатую передачу профилируют так,что к этому времени возникает зацепление между другой парой зубьев,и линия их контакта снова перемещается вдоль отрезка M1M2 .

183

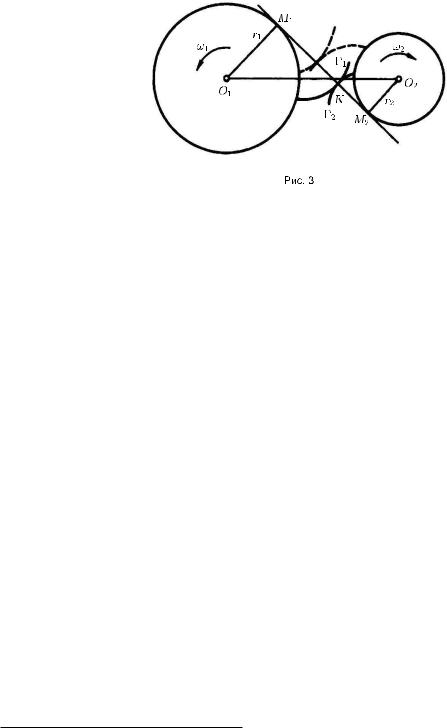
Если угловая скорость !2 ведущего колеса постоянна,то постоянна и скорость !2r2 движения точки K по линии,называемой линией зацепления.Но тогда постоянна и угловая скорость !1 = !2r2/r1 ведомого колеса.Таким образом,эвольвентное зацепление обеспечивает плавность вращения ведомого колеса и постоянство передаточного отношения !1/!2 = r2/r1 зубчатой передачи.Кроме того,некоторые изменения межосевого расстояния O1O2 ,вызванные неизбежными погрешностями при установке зубчатых колёс не влияют на передаточное отношение,если эти погрешности, конечно,не столь велики,что зубья колёс вообще не могут войти в зацепление.

§95.Элементарная поверхность.Простая поверхность.Общая поверхность

Определение. Область на плоскости называется элементарной областью,если она является образом открытого круга при топологическом отображении.Таким образом,элементарная область это область,гомеоморфная кругу.

Пусть γ простая замкнутая кривая на плоскости.Известна теорема Жордана10 о том,что простая замкнутая кривая на плоскости разбивает плоскость на две области и является границей для каждой из этих областей.Одна из областей конечна,другая бесконечна.Оказывается,конечная область гомеоморфна кругу.Таким образом,внутренность квадрата,прямоугольника,эллипса элементарные области.

Определение. Множество точек Φ пространства называется элементарной поверхностью,если оно является образом элементарной области на плоскости при топологическом отображении ее в пространство.

Пусть Φ элементарная поверхность и G элементарная область в плоскости,образом которой при топологическом отображении f является поверхность Φ. Пусть u и v декартовы координаты произвольной точки,принадлежащей области, x, y, z координаты соответствующей точки поверхности.Координаты x, y, z точки поверхности есть функции координат точки области G:

x = f1(u, v), y = f2(u, v), z = f3(u, v).

Определение. Эта система равенств,задающая отображение f области G в пространство,называется уравнениями поверхности в параметрической форме, u и v

называются криволинейными координатами на поверхности.

Определение. Координатными линиями данной поверхности называют линии на поверхности,соответствующие прямым u = const и v = const.

10Мари Энмон Камилл Жордан(1838–1922) французский математик,известный своими работами по алгебре,теории функций,топологии и кристаллографии.

184

Определение. Множество Φ точек пространства называется простой поверхностью,если это множество связно и каждая точка X этого множества имеет окрестность H такую,что часть Φ,расположенная в H ,является элементарной поверхностью.

Элементарная поверхность является простой поверхностью.Однако элементарными поверхностями далеко не исчерпываются все простые поверхности.Например, сфера является простой поверхностью,но не элементарной.

Простые поверхности нельзя охарактеризовать в целом общо и просто,как это было сделано для простых кривых.Некоторое представление о разнообразии простых поверхностей дает следующее рассуждение. Если из произвольной простой по-

верхности удалить замкнутое множество точек,но так,чтобы не нарушить связности оставшейся части,то эта оставшаяся часть будет также простой поверхностью.

Определение. Простая поверхность называется полной,если предельная точка для любой сходящейся последовательности точек поверхности также является точкой поверхности.

Например,сфера,параболоид полные поверхности,а сферический сегмент не является полной поверхностью(сферический сегмент без ограничивающей его

окружности).

Определение. Простая полная конечная поверхность на-

зывается замкнутой.

Кроме сферы,замкнутой поверхностью является, например,тор поверхность,получаемая вращением окружности вокруг прямой,лежащей в плоскости окружности и не пересекающей окружность.

Определение. Окрестностью точки X на простой поверхности Φ называется общая часть поверхности Φ и некоторой пространственной окрестности точки X .

Согласно определению,у каждой точки простой поверхности есть окрестность, которая является элементарной поверхностью.В дальнейшем,говоря об окрестности точки на поверхности,мы будем иметь в виду такую элементарную окрестность.

Определение. Множество Φ точек пространства называется общей поверхностью, если оно является образом простой поверхности при локально топологическом отображении ее в пространство.

Определение. Мы будем говорить,что отображение f1 простой поверхности Φ1 и отображение f2 простой поверхности Φ2 задают одну и ту же общую поверхность Φ,если между точками поверхностей Φ1 и Φ2 можно установить топологическое соответствие,при котором образы соответствующих точек этих поверхностей на поверхности Φ совпадают.

Пусть общая поверхность Φ является образом простой поверхности	¯	при ло-
	Φ
кально топологическом отображении f .

Определение. Окрестностью точки f(X) на поверхности Φ называется образ любой

окрестности точки на поверхности ¯ при отображении .

X Φ f

Так как отображение f в достаточно малой окрестности точки X является топологическим,то f(X) на Φ имеет окрестность,являющуюся элементарной поверхностью.Таким образом,исследование любой поверхности“в малом”сводится к рассмотрению элементарной поверхности.

185

§96.Регулярная поверхность.Аналитическое задание поверхности

Определение. Поверхность Φ называется регулярной (k раз дифференцируемой), если у каждой точки этой поверхности есть окрестность,допускающая регулярную параметризацию,то есть задание уравнениями в параметрической форме

x = f1(u, v), y = f2(u, v), z = f3(u, v),

где f1, f2, f3 регулярные( k раз непрерывно дифференцируемые)функции,заданные в элементарной области H плоскости uv.При k = 1 поверхность называется

гладкой.

Определение. Поверхность называется аналитической,если она в достаточно малой окрестности каждой своей точки допускает аналитическую параметризацию.

В дальнейшем мы будем рассматривать только регулярные поверхности. Регулярная поверхность в окрестности каждой своей точки может быть задана

уравнениями в параметрической форме

x = x(u, v), y = y(u, v), z = z(u, v),

где x, y, z регулярные функции переменных u, v,заданные в некоторой области G плоскости uv.Естественно возникает вопрос:когда система равенств

x = x(u, v), y = y(u, v), z = z(u, v),

где x, y, z регулярные функции переменных u, v в некоторой области G плоскости uv, задает поверхность?Ответ на него во многих случаях дает теорема.

Теорема96.1. Если x(u, v), y(u, v), z(u, v) регулярные функции в области G плоскости uv,удовлетворяющие условию,что ранг матрицы

xu yu zu

xv yv zv

всюду в G равен двум,то система равенств

x = x(u, v), y = y(u, v), z = z(u, v)

задает некотрую поверхность Φ.Эта поверхность есть образ простой поверхности G при локально топологическом отображении,которое точке (u, v) области G сопоставляет точку пространства с координатами x(u, v), y(u, v), z(u, v).

Доказательство. В доказательстве нуждается только утверждение об однооднозначности отображения.Докажем его.

Пусть утверждение неверно.Тогда существует точка (u0, v0) области G,в сколь угодно малой окрестности которой можно указать две различные точки (u1, v1) и (u2, v2) такие,что

x(u1, v1) − x(u2, v2) = 0, y(u1, v1) − y(u2, v2) = 0, z(u1, v1) − z(u2, v2) = 0.

Имеем

x(u1, v1) − x(u2, v2) = (x(u1, v1) − x(u1, v2)) + (x(u1, v2) − x(u2, v2)) = = (v1 − v2)xv(u1, 1) + (u1 − u2)xu( 10 , v2) = 0.

186

Аналогично

y(u1, v1) − y(u2, v2) = (v1 − v2)yv(u1, 2) + (u1 − u2)yu( 20 , v2) = 0.

z(u1, v1) − z(u2, v2) = (v1 − v2)zv(u1, 3) + (u1 − u2)zu( 30 , v2) = 0.

Так как u1 − u2 , v1 − v2 не равны нулю одновременно,из полученных равенств заключаем,что ранг матрицы

xu( 10 , v2)	yu( 20 , v2)	zu( 30 , v2)
xv(u1, 1)	yv(u1, 2)	zv(u1, 3

меньше двух,то есть ее миноры второго порядка равны нулю.По непрерывности функций xu, xv, . . . , zv отсюда следует,что все миноры второго порядка матрицы

xu yu zu

xv yv zv

в точке (u0, v0) равны нулю,то есть ранг матрицы меньше двух.Противоречие доказывает утверждение теоремы.

Некоторые поверхности при подходящем выборе осей координат x, y, z допускают параметризацию для всей поверхности вида

x = u, y = v, z = f(u, v),

где f(u, v) функция,определенная в области G плоскости uv.Уравнения этой поверхности могут быть записаны в эквивалентной форме z = f(x, y).

Такая параметризация поверхности отличается наглядностью.Соответствие между точками поверхности и точками плоскости xy осуществляется проектированием прямыми,параллельными оси z.

Мы будем говорить,что поверхность Φ неявно задана уравнением '(x, y, z) = 0, выражая этим только то,что координаты точек поверхности удовлетворяют данному уравнению.При этом могут существовать точки пространства,удовлетворяющие данному уравнению и не принадлежащие поверхности Φ.

Теорема96.2. Пусть '(x, y, z) регулярная функция переменных x, y, z.Пусть

M множество точек пространства,удовлетворяющих уравнению	'(x, y, z) = 0	,
(x0, y0, z0) точка этого множества,в которой 'x2 + 'y2 + 'z2 6= 0	.Тогда у точ-

ки (x0, y0, z0) есть окрестность такая,что все точки M ,принадлежащие этой окрестности,образуют регулярную элементарную поверхность.

Доказательство. Пусть для определенности 'z 6= 0 в точке (x0, y0, z0).По теоре-

ме о неявной функции существуют	числа δ,">	0 и регулярная функция	(x, y),
определенная в области |x − x0| < δ ,|y − y0| < δ		,такие,что все точки (x, y,	(x, y)),

|x − x0| < δ ,|y − y0| < δ удовлетворяют уравнению '(x, y, z) = 0,причем этими точками исчерпываются все точки параллелепипеда |x −x0| < δ ,|y −y0| < δ ,|z −z0| < ", удовлетворяющие уравнению '(x, y, z) = 0.Элементарная поверхность,о которой идет речь в теореме,задается уравнением z = (x, y).

187

ЛЕКЦИЯ29.ОСОБЫЕ ТОЧКИ.КАСАТЕЛЬНАЯ ПЛОСКОСТЬ

§97.Особые точки регулярной поверхности

Определение. Точка P регулярной поверхности называется обыкновенной точкой по отношению к данной степени регулярности k,если в окрестности этой точки поверхность допускает k раз дифференцируемую параметризацию

x = x(u, v), y = y(u, v), z = z(u, v),

удовлетворяющую условию:ранг матрицы
xu	yu	zu
xv	yv	zv

в точке P равен двум.В противном случае точка P называется особой.

Линия на поверхности,все точки которой являются особыми точками,называ-

ется особой линией.

Для поверхностей исследование особых точек провести гораздо труднее,чем для кривых.Рассмотрим только простейшие случаи.

Пусть

x= x(u, v), y = y(u, v), z = z(u, v)

регулярная параметризация поверхности в окрестности точки Q.Пусть ранг мат-

рицы

xu yu zu xv yv zv

всюду в окрестности Q равен двум,кроме самой точки Q,в которой он меньше двух. Запишем уравнение поверхности в векторном виде

r = r(u, v), где r(u, v) = x(u, v)e1 + y(u, v)e2 + z(u, v)e3,

(e1, e2, e3 единичные векторы,направленные по осям x, y, z).Тогда условие того, что ранг приведенной матрицы равен двум или меньше двух,сводится к тому,что [ru, rv] 6= 0 или [ru, rv] = 0 соответственно.

Рассмотрим вектор-функцию

w = [ru, rv] .

|[ru, rv]|

Докажем,что она инвариантна относительно замен координат с якобианом больше нуля,а при замене координат с якобианом меньше нуля она только меняет знак.

Сделаем замену переменных

u = u( ,β ), v = v( ,β ),

где u и v регулярные функции ,β .Тогда R( ,β ) = r(u( ,β ), v( ,β )) регулярная функция ,β .Имеем

R = ruu + rvv , Rβ = ruuβ + rvvβ.

188

Тогда

[R , Rβ]

[ruu + rvv , ruuβ + rvvβ]

W =

=

=

|[R , Rβ]|

|[ruu + rvv , ruuβ + rvvβ]|

"

[ru, rv] ·

"

u

uβ

[ru, rv]u vβ + [rv, ru]v uβ

v

vβ

"

"

"

|

|

[ru, rv]

·

v

vβ

=

=

"

"

"

= w.

[ru, rv]u vβ + [rv, ru]v uβ

"

u

uβ

""

±

"

"

"

!

"

""

Утверждение. Если wP

не стремится"к определенному"

""пределу при P

Q

,

точка Q поверхности будет особой.

Доказательство.

В самом деле,если Q обыкновенная точка,то в ее окрестности

может быть введена регулярная параметризация ( ,β ) такая,что

[r , rβ] 6= 0 в точке

Q и,следовательно,при P ! Q

[r , rβ]

= ±

[ru, rv]

|[r , rβ]|

|[ru, rv]|

стремится к определенному пределу.

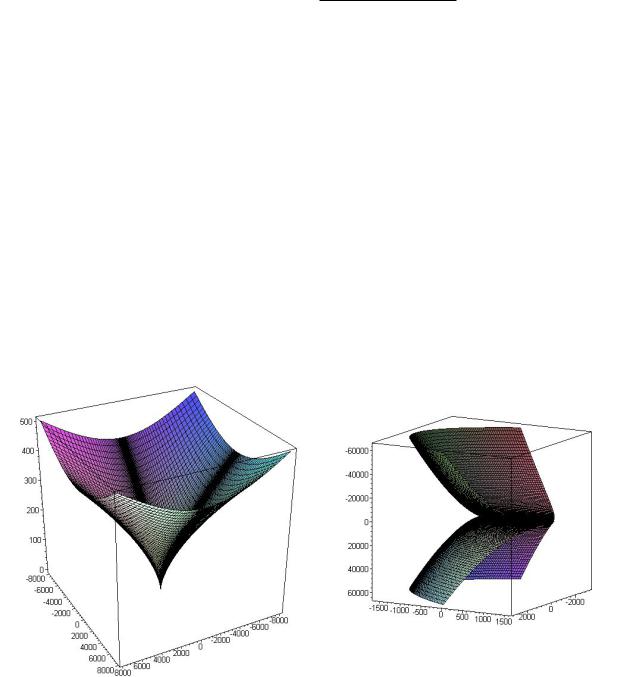
Пример97.1. Точка (0, 0) на поверхности

x = u3, y = v3, z = (u6 + v6)1/3

является особой точкой. w(u, v) не стремится к определенному пределу,когда u и v произвольным образом стремятся к нулю(рис. 1).

Рис. 1 Рис. 2

Допустим теперь,что при P ! Q wP стремится к определенному пределу wQ . Тогда рассмотренный только что признак не дает ответа на вопрос,будет ли точка Q особой или обыкновенной.

Пусть криволинейные координаты точки Q u0 и v0 .Возьмем в плоскости uv малый простой контур γ¯ ,охватывающий точку (u0, v0).Пусть γ соответствующий контур на поверхности.Спроектируем контур γ на плоскость & ,проходящую через точку Q,перпендикулярную вектору wQ .Если проекция γ˜ контура γ на плоскость

189

& не охватывает точки Q или охватывает ее более одного раза,то Q заведомо особая точка.

Допустим,что утверждение неверно,и Q обыкновенная точка.Тогда поверхность допускает параметризацию r = r( ,β ),удовлетворяющую в Q условию [r , rβ] 6= 0,откуда следует,что r и rβ неравные нулю и не параллельные векторы.

Пусть = 0 + (t), β = β0 + (t) уравнение контура γ .Тогда контур в плоскости & ,заданный уравнением

r = r(Q) + (t)r (Q) + (t)rβ(Q)

мало отличается от γ˜ .И так как этот контур получается аффинным преобразованием из γ¯ ,то он,а с ним и γ˜ один раз охватывает точку Q подобно тому как контур γ¯ охватывает точку ( 0, β0).

Пример97.2. Точка (0, 0) на поверхности

x = u2 − v2, y = 2uv, z = u5

является особой(рис. 2).

При обходе окружности γ¯ u2 + v2 = "2 соответствующая точка γ˜ проходит

дважды окружность x2 + y2		= "4 .Это сразу же видно,если рассмотреть такую
параметризацию окружности:		u = " cos t, v = " sin t.Действительно,тогда имеем:
x = "2 cos 2t, y = "2 sin 2t.Таким образом, γ˜ охватывает точку (0, 0) дважды.
Пример97.3. Все точки поверхности
		x = u, y = v2, z = v3,
расположенные на оси x-ов( v = 0)являются особыми(рис. 3).
Здесь плоскость & является плоскостью xy.Контур			γ соответствующей окруж-
ности2	γ¯ : (x − a)2 + y2 = "2 располагается целиком в полуплоскости y ≥ 0 (так как
y = v	)и,следовательно,ни разу не охватывает точку		Q(a, 0) оси x-ов.

Определение. Особая линия типа,рассмотренного в этом примере,называется реб-

ром возврата поверхности.

Каждая плоскость,перпендикулярная ребру возврата,пересекает поверхность по кривой,для которой точка ребра возврата является особой точкой точкой возврата.В рассмотренном примере такими сечениями являются полукубические параболы.

Рассмотрим теперь поверхность,заданную уравнением '(x, y, z) = 0.

Особыми точками этой поверхности могут быть только те точки,где 'x = 'y = 'z = 0.Действительно,если в точке Q поверхности одна из частных производных,

например, 'z 6= 0,то поверхность в окрестности точки	Q допускает регулярную
параметризацию вида z = (x, y),откуда следует,что	Q является обыкновенной
точкой.

Пусть 'x = 'y = 'z = 0 в точке поверхности Q(x0, y0, z0).Раскладывая функцию ' по формуле Тейлора в окрестности точки Q,получим

a11(x − x0)2 + a22(y − y0)2 + a33(z − z0)2+

+2a12(x − x0)(y − y0) + 2a13(x − x0)(z − z0) + 2a23(y − y0)(z − z0) + R = 0.

Если квадратичная форма P aij i j является определенной,то есть обращается в нуль только когда все k равны нулю,то в достаточно малой окрестности точки

190