geometry24

для некоторых , 0, β , β0, γ , γ0

8

< s = a + 0a0,

s = βb + β0b0, : s = γc + γ0c0.

Заметим,что для этого было необходимо несовпадение a и a0 и т.д.Тогда

8

< u = βb − γc = γ0c0 − β0b0,

v = γc − a = 0a0 − γ0c0, : w = a − βb = β0b0 − 0a0.

Таким образом, u отвечает точке,лежащей и на прямой BC ,и на B0C0 ,то есть Q. Аналогично v некоторый представитель координат R, а w P .Сложив почленно равенства,определяющие u, v и w,получим u+v+w = (0, 0, 0),то есть точки лежат на одной прямой(плоскости связки).

Доказательство достаточности. Переформулируем доказанное утверждение в следующем виде.

Пусть на проективной плоскости заданы две тройки точек ABC и A0B0C0 , ни одна из которых не инцидентна одной прямой.Обозначим через A, B, C, A0 , B0 , C0 прямые,инцидентные B и C , A и C , A и B , B0 и C0 , A0 и C0 , A0 и

B0

,и пусть

6

, A6A

,

6

, B6B

,

6

, C6C

.Обозначим через

A = A0

=

0

B = B0

= 0

C = C0

= 0

a, b, c прямые,инцидентные точкам

A и A0 ,

B и B0 , C и C0 соответственно.

Обозначим через A, B и C точки,инцидентные прямым

A и A0 , B и B0 и C и C0

соответственно.Пусть три прямые

a, b, c инцидентны одной точке.Тогда три

точки A, B и C инцидентны одной прямой.

По принципу двойственности мы доказали тем самым следующее двойственное

утверждение.

Пусть на проективной плоскости заданы две тройки прямых ABC и A0B0C0 ,

ни одна из которых не инцидентна одной точке.Обозначим через A, B, C, A0, B0, C0

точки,инцидентные

B и C, A и C,

A и B, B0

и C0 , A0 и C0 , A0 и B0 ,и пусть

6

, A6A

,

6

, B6B

,

6

, C6C

0

.Обозначим через A, B и C точки,

A = A0

=

0

B = B0

=

0

C = C0

=

инцидентные прямым A и A0 , B и B0 , C и C0

соответственно.Обозначим через

a, b, c прямые,инцидентные точкам

A и A0 ,

B и B0 , C и C0 соответственно.

Пусть три точки A, B и C инцидентны одной прямой.Тогда три прямые a, b, c инцидентны одной точке.

Но это и есть обратное утверждение.

§71.Проективная система координат в связке и на проективной плоскости

Рассмотрим связку с центром O.

Определение. Две аффинных системы координат Oe1e2e3 и Oe01e02e03 называются эквивалентными,если для некоторого ненулевого числа λ e01 = λe1 , e02 = λe2 , e03 = λe3 .

Утверждение. Каждый луч связки имеет одни и те же однородные координаты относительно двух систем Oe1e2e3 и Oe01e02e03 тогда и только тогда,когда эти системы эквивалентны.

Доказательство. Достаточность очевидна.

Необходимость.Луч,на котором лежит вектор e01 ,имеет в системе координат Oe01e02e03 координаты {1 : 0 : 0},следовательно,его координатами в обеих системах

131

будут тройки вида λ1, 0, 0,где

λ1 6= 0.Значит,поскольку в системе

Oe1e2e3 этот

вектор имеет координаты

1

1 6

, то

1

1

1 .Аналогично

2

2

2 ,

(λ

, 0, 0) (λ

= 0)

e0

= λ

e

e0

= λ

e

e30 = λ3e3 .Луч,на котором лежит вектор e0

= e10

+ e20 + e30 имеет в обеих системах

одни и те же координаты {1 : 1 : 1},так что имеем равенство

2

e0 = λ(e1 + e2 + e3)

для некоторого

6

.Так как с другой стороны

e0

1

1

2

3

3 , то

1

λ = 0

= λ

e

+ λ

e

+ λ

e

λ = λ

=

λ2 = λ3 ,и утверждение доказано.

Определение. Проективной системой координат в связке O называется класс эквивалентных между собой аффинных систем координат с началом в O.

Определение. Задать проективную систему координат в связке значит,задать в

этой связке три некомпланарных координатных луча		¯	¯	¯	и четвертый еди-
		X1	, X2	, X3
¯	,некомпланарный ни с какими двумя из лучей			¯	¯	¯
ничный луч E				X1	, X2	, X3 .

Доказательство. Докажем эквивалентность определений проективной системы координат.

Сначала докажем,что проективная система координат в смысле первого определения является проективной системой координат в смысле второго определения.

Вместо задания единичных векторов можно задать оси координат ¯ ¯ ,

OXi = OEi

где ei = OEi , i = 1, 2, 3 и точку E(1, 1, 1) единичную точку данной аффинной системы координат.Проекции этой точки на оси координат(проекции берутся параллельно плоскости двух других осей координат)определяют единичные векторы OEi = ei ,причем OE = OE1 + OE2 + OE3 .Очевидно,что две аффинные системы координат тогда и только тогда эквивалентны,когда у них одинаковые оси,а единичные точки лежат на одном и том же луче единичном луче связки.

Теперь докажем,что проективная система координат в смысле второго определения является проективной системой координат в смысле первого определения.

¯		¯ ¯ ¯ ¯
На единичном луче E данной проективной координатной системы		X1X2X3E
¯	соответственно.По-
возьмем точку E ,обозначим через Ei ее проекции на лучи Xi
лучим векторы ei = OEi (рис. 2).Аффинная система координат	Oe1e2e3 и все ей эк-
вивалентные системы очевидно определяют данную проективную систему		¯ ¯ ¯ ¯
		X1X2X3E .

Каждая система координат,входящая в данный класс эквивалентных систем,опре-

деляется заданием точки на единичном луче ¯ .

E E

132

Определение. Тройками проективных координат луча связки O в проективной си-

стеме ¯ ¯ ¯ ¯ называются тройки однородных координат данного луча в аффин-

X1X2X3E

ной системе координат Oe1e2e3 или в любой эквивалентной ей системе.

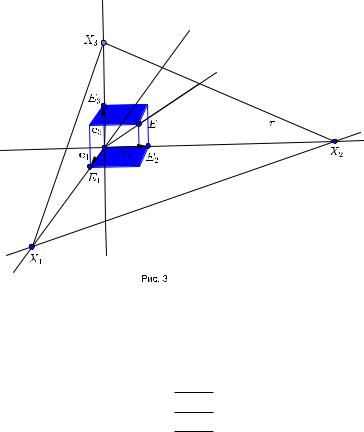
Посредством перспективного отображения на плоскость ¯ получаем точки X1, X2, X3 вершины координатного треугольника,и единичную точку E (рис. 3).

Определение. Четыре точки X1, X2, X3, E называются фундаментальными (или базисными)точками данной проективной системы координат на плоскости.

Очевидно,что вершины и стороны координатного треугольника имеют координаты:

X1 = (1 : 0 : 0), X3X2 = {1 : 0 : 0}

X2 = (0 : 1 : 0), X1X3 = {0 : 1 : 0}

X3 = (0 : 0 : 1), X1X2 = {0 : 0 : 1}

133

ЛЕКЦИЯ21.ЗАМЕНЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ

§72.Замены координат на проективной плоскости

Рассмотрим следующую задачу.

Задача. Пусть в связке O (или плоскости )даны две координатные системы:

“старая” X1, X2, X3, E и“новая” X10 , X20 , X30 , E0 ,причем известны координаты фундаментальных точек“новой системы” X10 , X20 , X30 , E0 в“старой”системе:

X10 = (c11 : c21 : c31), X20 = (c12 : c22 : c32), X30 = (c13 : c23 : c33), E0 = ("1 : "2 : "3).

Найти выражения координат x1, x2, x3 произвольной точки M относительно“старой”системы координат через координаты x01, x02, x03 той же точки в“новой”системе координат.

Решение. Предположим сначала,что тройки координат точек X10 , X20 , X30 , E0 выбраны согласованными,то есть такими,что выполняется векторное равенство

(c11 : c21 : c31) + (c12 : c22 : c32) + (c13 : c23 : c33) = ("1 : "2 : "3).

¯
Выберем на луче E какой-нибудь ненулевой вектор OE = e и возьмем его проек-
¯	¯	¯
ции e1 = OE1, e2 = OE2, e3 = OE3 на лучи X1	, X2	, X3 .Тогда Oe1e2e3 есть аффинная
система координат в связке,задающая проективную систему координат X1X2X3E .

Каждая тройка x1, x2, x3 проективных координат в системе X1X2X3E луча m есть тройка однородных координат в аффинной системе Oe1e2e3 некоторого направляющего вектора u этого луча.

Проективную систему координат X10 X20 X30 E0 задает аффинная система координат в связке O с единичными векторами

e01 = (c11, c21, c31), e02 = (c12, c22, c32), e03 = (c13, c23, c33)

(их координаты даны в системе Oe1e2e3 ).

С другой стороны,тройка координат x01, x02, x03 вектора u в системе X10 X20 X30 E0 есть тройка координат(в аффинной системе координат Oe01e02e03 )какого-то направ-

ляющего вектора u0 = λu того же луча m.Поэтому имеем

		x0		x0		x0
	x1 = c11	1	+ c12	2	+ c13	3	,
		λ		λ		λ
		x0		x0		x0
	x2 = c21	1	+ c22	2	+ c23	3	,
		λ		λ		λ
		x0		x0		x0
	x3 = c31	1	+ c32	2	+ c33	3	,
		λ		λ		λ

или

λx1 = c11x01 + c12x02 + c13x03, λx2 = c21x01 + c22x02 + c23x03, λx3 = c31x01 + c32x02 + c33x03.

Это и есть формулы перехода от проективной системы X1X2X3E к проективной системе X10 X20 X30 E0 в предположении,что для координатной записи фундаментальных точек X10 , X20 , X30 , E0 относительно системы X1X2X3E выбраны согласованные тройки координат.

134

Предположим теперь,что выбраны произвольные(не согласованные)тройки координат.Тогда их надо заменить определяющими те же точки согласованными тройками,т.е.выбрать ненулевые множители λ1, λ2, λ3 ,такие,что

X10 = (λ1c11, λ1c21, λ1c31), X20 = (λ2c12, λ2c22, λ2c32), X30 = (λ3c13, λ3c23, λ3c33),

и чтобы имело место векторное равенство

(λ1c11, λ1c21, λ1c31) + (λ2c12, λ2c22, λ2c32) + (λ3c13, λ3c23, λ3c33) = ("1, "2, "3).

Это равенство равносильно системе уравнений относительно λ1, λ2, λ3 :

8

< c11λ1 + c12λ2 + c13λ3 = "1,

:c21λ1 + c22λ2 + c23λ3 = "2, c31λ1 + c32λ2 + c33λ3 = "3.

Определитель этой системы отличен от нуля,так как столбцы матрицы коэффициентов линейно независимы.Решение системы единственно,и его можно найти по формулам Крамера.При этом ни одно из чисел λj не равно нулю,поскольку никакие три из точек X10 , X20 , X30 , E0 не лежат на одной прямой.

Находим λ1, λ2, λ3 и уже с помощью согласованных троек координат записываем формулы преобразования координат:

λx1 = c011x01 + c012x02 + c013x03, λx2 = c021x01 + c022x02 + c023x03, λx3 = c031x01 + c032x02 + c033x03,

где

c110	= λ1c11, c120		= λ2c12, c130		= λ3c13,
c210	= λ1c21,	c220	= λ2c22,	c230	= λ3c23,
c310	= λ1c31,	c320	= λ2c32,	c330	= λ3c33.

Замечание. Формально можно считать,что проективная система координат на плоскости задается невырожденной матрицей C .Считая при этом,что имеется исходная проективная система координат x1, x2, x3 (скажем,система однородных координат),мы получим выражения проективных координат произвольной точки M через ее координаты в исходной системе кооринат:

x10	A	x1	A
@ x30		@ x3
0 x20	1	= λC−1 0 x2	1 .

Тем самым,проективные координаты являются обобщением однородных координат.Однородные координаты(на прямой,на плоскости,в пространстве)являются специальным случаем проективных координат,когда одна(для прямой),две (на плоскости)или три(в пространстве)из фундаментальных точек сдвигаются в бесконечно удаленную точку.

Рассматривая проективные координаты точки на плоскости как однородные координаты лучей в связке,мы рассматриваем проективную геометрию только как часть аффинной геометрии пространства,как геометрию конкретно выбранной в нем связки.Такой подход может иметь место,но следует помнить о сказанном выше.

135

§73.Проективные преобразования

Определение. Всякое аффинное преобразование пространства,оставляющее центр связки O на месте,отображает прямые,проходящие через O,в некоторые другие прямые,проходящие через O.Возникающее таким образом отображение связки в себя называется проективным.

Непосредственно из определения следует,что проективное преобразование переводит прямые проективной плоскости в прямые,сохраняя отношение инцидентности.

Если C матрица проективного преобразования в репере Oe1e2e3 ,то в соответствующих однородных координатах проективное преобразование запишется в виде

x˜1	A	x1	A
@ x˜3		@ x3
λ 0 x˜2	1	= C 0 x2	1 ,

где λ произвольный ненулевой множитель.В соответствующих аффинных координатах на плоскости

x˜ =

x˜1

=

c11x1 + c12x2 + c13x3

=

c11x + c12y + c13

,

(73.1)

x˜3

c31x1 + c32x2 + c33x3

c31x + c32y + c33

y˜ =

x˜2

=

c21x1 + c22x2 + c23x3

=

c21x + c22y + c23

.

(73.2)

x˜3

c31x1 + c32x2 + c33x3

c31x + c32y + c33

Пусть при проективном преобразовании ' проективной плоскости фундаментальная четверка Y1Y2Y3E некоторой проективной системы координат переходит в четверку точек Y10Y20Y30E0 .Эти четыре точки не лежат на одной прямой,поскольку отношение инцидентности сохраняется.Следовательно,они также определяют проективную систему координат.

Лемма73.1. Пусть M произвольная точка плоскости, M0 ее образ при проективном преобразовании '.Тогда M0 имеет относительно системы координат Y10Y20Y30E0 те же координаты,что M имела относительно системы Y1Y2Y3E .

Доказательство. Пусть координаты точек Y1, Y2, Y3, E в исходной системе координат X1X2X3E

Y1 = (a1 : a2 : a3), Y2 = (b1 : b2 : b3), Y3 = (c1 : c2 : c3), E = ("1 : "2 : "3),

причем тройки координат выбраны согласованно,т.е.

{a1 : a2 : a3} + {b1 : b2 : b3} + {c1 : c2 : c3} = {"1 : "2 : "3}.

Тогда однородные координаты x1, x2, x3 произвольной точки M связаны с координатами y1, y2, y3 той же точки в системе Y1Y2Y3E соотношениями

8

< λx1

:λx2 λx3

=a1y1

=a2y1

=a3y1

+ b1y2 + c1y3,

+ b2y2 + c2y3, (73.3)

+ b3y2 + c3y3.

Проективное преобразование ' задано тем,что наряду с исходной однородной системой координат X1X2X3E дана система X10 X20 X30 E0 ,так что тройки координат

136

M0 относительно системы X10 X20 X30 E0						есть не что иное,как тройки координат M
относительно системы X1X2X3E .
Это верно для любой точки M ,в частности,для точек										Y1, Y2, Y3, E :тройки коор-
динат точек	1	2	3	, E0	относительно системы		1	2	3E	0	пропорциональны трой-
	Y 0	, Y 0	, Y 0			X0		X0	X0

кам однородных координат точек Y1, Y2, Y3, E ,т.е.соответственно тройкам a1, a2, a3 , b1, b2, b3 , c1, c2, c3 , "1, "2, "3 .Значит,формулы преобразования координат,соответству-

ющие переходу от системы

1

2

3E

0

к системе

1 2 3

имеют ту же матрицу ко-

X0

X0

X

0

Y 0Y 0Y 0E0

эффициентов,что и преобразование(73.3).Поэтому,обозначая через

y10 , y20 , y30 коор-

динаты точки

M0

в системе

1 2

3

и помня,что в системе 1

2

3E

0

координаты

Y 0Y 0Y 0E0

X0

X0

X0

точки M0 есть x1, x2, x3 ,будем иметь

8

λx10

= a1y10 + b1y20 + c1y30 ,

(73.4)

λx20

= a2y10 + b2y20

+ c2y30 ,

:

= a3y10 + b3y20 + c3y30 .

< λx30

Отсюда,ввиду однозначной разрешимости систем уравнений(73.3)и(73.4)относительно y1, y2, y3 и y10 , y20 , y30 соответственно,следует утверждение леммы.

Теорема73.1. (основная теорема о проективных преобразованиях плоско-

сти). Пусть Y1Y2Y3E и Y10Y20Y30E0 две четверки точек проективной плоскости, удовлетворяющие тому условию,что никакие три точки,принадлежащие одной и той же четверке,не инцидентны одной прямой.Тогда существует ровно одно проективное преобразование,переводящее одну из них в другую.

Доказательство. Будем рассматривать эти четверки как фундаментальные четверки двух координатных систем.Поставим в соответствие каждой точке M ту точку M0 ,которая относительно координатной системы Y10Y20Y30E0 имеет те же самые тройки координат,которые точка M имела относительно системы Y1Y2Y3E .Получим проективное преобразование,переводящее точки Y1, Y2, Y3, E в точки Y10, Y20, Y30, E0 соответственно.

Это преобразование единственно,так как,по лемме,тройки координат точки '(M) относительно системы Y10Y20Y30E0 суть не что иное,как тройки координат точки M относительно системы Y1Y2Y3E для любого проективного преобразования '.

Следствие73.1. Для любой прямой существует проективное преобразование,переводящее ее в несобственную.

Легко доказать,что центральная проекция плоскости на плоскость является проективным преобразованием.

§74.Проективно-аффинные преобразования

Определение. Проективное преобразование ' пополненной плоскости(то есть плоскости,у которой выделена несобственная прямая),переводящее эту выделенную прямую в себя,называется проективно-аффинным.

Очевидно,что для того,чтобы проективное преобразование было проективноаффинным,необходимо и достаточно,чтобы две несобственные точки перешли в несобственные.Поскольку прямая переходит в прямую,в частности,несобственная, то никакая собственная точка не может отобразиться в несобственную.Поэтому можно дать следующее определение.

Определение74.1. Пусть ' проективно-аффинное преобразование.Обозначим через '0 ограничение ' на собственные точки,то есть непополненную плоскость. Тогда преобразование '0 отображает непополненную плоскость на себя.

137

Утверждение. Отображение '0 является аффинным.

Доказательство. Пусть введены однородные координаты и x3 = 0 несобственная прямая.Пусть ' имеет матричную запись

λx˜1 = c11x1 λx˜2 = c21x1 λx˜3 = c31x1

+c12x2 + c13x3,

+c22x2 + c23x3,

+c32x2 + c33x3.

Если при любых x1 и x2 из x3 = 0 следует x˜3

= 0,то c31 = c32 = 0 и из(73.1)и

(73.2)получаем

c12

c13

x˜ =

c11

x +

y +

c33

c33

c33

y˜ =

c21

x +

c22

y +

c23

.

c33

c33

c33

§75.Проективная прямая

Проективная прямая(прямая,пополненная одной точкой)определяется аналогичным образом.Роль ее модели теперь играет собственный пучок прямых на плоскости,так что прямая пучка,параллельная пополняемой прямой,соответствует бесконечно удаленной точке.Проективное преобразование в однородных координатах записывается формулами

λx˜1 = c11x1 + c12x2,	, det C = det[cij] 6= 0.
λx˜2 = c21x1 + c22x2.

Напомним,что простым отношением трех различных точек A1, A2 и A3 на пря-

мой называется число λ: A1A3 = λA2A3 , λ = A1A3 .

A2A3

Определение. Двойное(или сложное,ангармоническое)отношение четырех различных точек A1, A2, A3 и A4 на прямой это

(A1A2A3A4) =		A1A3	:		A1A4	.
		A2A3
				A2A4
В аффинных координатах
(A1A2A3A4) =	x3 − x1		:		x4 − x1		.
	x3 − x2			x4 − x2

Очевидны свойства двойного отношения: 1) (A1A2A3A4) = (A3A4A1A2);

1

2) (A1A2A4A3) = (A1A2A3A4) .

Доопределим двойное отношение

(A	A	A		1	) =	A1A3	=	x3 − x1	.
						A2A3
1	2		3				x3 − x2

Лемма75.1. В соответствующих однородных координатах (x : y):

	"	y1	y3	"		"		y1	y4	"
	"	x1	x3	"		"		x1	x4	"
		x2	x3					x2	x4
	"	y2	y3	"		"		y2	y4	"
	"			"		"				"
(A1A2A3A4) =	"			"	:		"			"	.
	"			"		"				"
	"			"		"				"
	"			"		"				"

138

Доказательство. Правая часть определена корректно,то есть не меняется при заменах (xi, yi) ! (λxi,λy i) и совпадает с формулой в аффинных координатах при yi = 1,причем,если y4 = 0,то имеем формулу для (A1A2A31).

Замечание. Можно использовать следующее простое правило для запоминания определителей,стоящих в числителе и знаменателе формулы для двойного отношения.В четверостишиях различают перекрестные рифмы,когда рифмуются первая и третья,вторая и четвертая строки,и опоясывающие рифмы,когда рифмуются первая и четвертая,вторая и третья строки.

Пример перекрестной рифмы:Меж тем Онегина явленье У Лариных произвело

На всех большое впечатленье, И всех соседей развлекло.

Пример опоясывающей рифмы:Иные даже утверждали, Что свадьба слажена совсем, Но остановлена затем,

Что модных к´олец не достали. (Оба четверостишия из поэмы А.С.Пушкина“Евгений Онегин”.)

Определители,стоящие в числителе,построены по принципу перекрестных рифм: (1,3),(2,4),стоящие в знаменателе по принципу опоясывающих: (1,4), (2,3).

Теорема75.1. Двойное отношение точек на проективной прямой не зависит от выбора проективных координат.

x		x	имеем
Доказательство. При замене вида λ y		= C y00

	λixi λjxj						xi0
	λiyi			λjyj		= C yi0
	"	xi		xj	"		"	xi0
λiλj "		yi		yj	" = det C		"	yi0
	"				"		"
Подставляя,видим,что λi и det"			C сокращаются" ".

x00j , yj

"

x00j """ . yj

Следствие75.1. Двойное отношение не меняется при проективных преобразованиях прямой.

Простое отношение не сохраняется при проективных преобразованиях(в отличие от аффинных).Более полный результат дает следующая теорема.

Теорема75.2. Для любых двух троек различных точек A1, A2, A3 и A01, A02, A03 на прямой существует и единственно такое проективное преобразование f ,что f(Ai) = A0i , i = 1, 2, 3.

Доказательство. В модели пучка прямых выберем на прямых вектора так,что e2 = e1 + e3 , e02 = e01 + e03 .Проективное преобразование отвечает паре реперов Oe1e3

и Oe01e03 (рис. 1).

139

Докажем единственность.Пусть имеется наряду с построенным преобразованием ' и другое .Тогда имеется точка A4 ,такая,что '(A4) 6= (A4).Но положение образа точки A4 полностью определяется двойным отношением A4 с A1, A2, A3 , так как двойное отношение инвариантно при замене координат,а следовательно,и при преобразовании.

Лемма75.2. Пусть li (i = 1, 2, 3, 4) четыре прямых из одного пучка на проективной плоскости,а прямая l этому пучку не принадлежит.Обозначим точки пересечения l с li через Ai (i = 1, 2, 3, 4).Тогда двойное отношение (A1A2A3A4) зависит только от li и не зависит от l (рис. 2).

Доказательство. Если рассмотреть другую прямую,то лучи пучка осуществляют проективное преобразование(центральная проекция),переводящие точки пересечения с l в точки пересечения с другой прямой.По теореме75.1двойное отношение сохраняется.

§76.Кривые второго порядка на проективной плоскости

Кривая второго порядка на проективной плоскости определяется однородным уравнением второго порядка в некоторой однородной системе координат:

q(x) = a11x21 + 2a12x1x2 + 2a13x1x3 + a22x22 + 2a23x2x3 + a33x23 = 0.

140