geometry24

Геометрически умножение вектора a на положительное число > 1 состоит в растягивании вектора a в раз.Аналогично можно придать смысл умножению на положительное < 1 и отрицательное .Так,при отрицательном , | | < 1 происходит сжатие вектора и изменение его направления на противоположное.Тем не менее,мы будем во всех этих случаях говорить о“растяжении”вектора a в раз.

Если = 0 или a = 0, то a = 0.

Свойства линейных операций над векторами

1. a + b = b + a (коммутативность сложения правило параллелограмма);

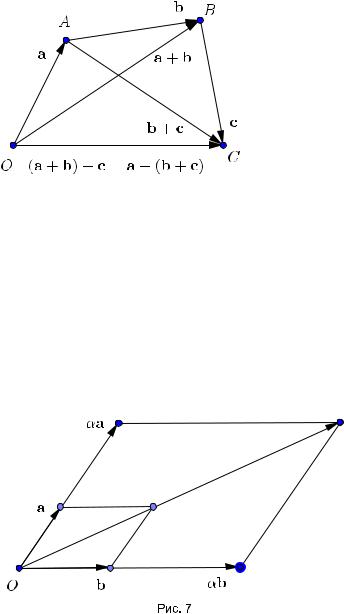
Доказательство. Отложим векторы OA = a и OB = b от произвольной точки O. Отложим от точки B вектор BC = a (рис. 5).Поскольку отрезки BC и OA равны и параллельны,то четырехугольник OBCA параллелограмм.Следовательно, AC = b.Из определения суммы векторов и рассмотрения треугольника OBC следует,что

OC = OB + BC = b + a.

Аналогично из треугольника OAC получаем:

OC = OA + AC = a + b,

что и доказывает первое свойство.

2. (a+ b) + c = a+ (b+ c) (ассоциативность сложения правило четырехугольника);

11

Доказательство. Отложим от точки O вектор OA = a,от точки A вектор AB = b,от точки B вектор BC = c (рис. 6).Тогда

(a + b) + c = (OA + AB) + BC = OB + BC = OC,

a + (b + c) = OA + (AB + BC) = OA + AC = OC,

что и доказывает второе свойство.

3. a + 0 = a (существование нулевого век-

тора);

Это свойство сразу же следует из определений суммы векторов и нулевого вектора.

4. a + (−1) · a = 0 (существование противоположного вектора);

Это свойство сразу же следует из определе-

ний умножения вектора на число и суммы век-

торов.

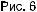5. (βa) = (β)a (ассоциативность); Доказательство. Это свойство геометрически обозначает,что при“растяжении” вектора a сначала в раз,а потом в β раз получается такой же вектор,как и при “растяжении”вектора a в β раз.

Замечание. Здесь и далее“растяжение”понимаем в том смысле,как это было описано в определении умножения вектора на число.

6. ( + β)a = a + βa (дистрибутивность1);

Доказательство. И это свойство практически очевидно из наглядных геометрических соображений.При“растяжении”вектора a в + β раз получается такой же

вектор,как при сложении вектора a, “растянутого”в	раз,с вектором a, “растяну-
тым”в β раз.	7. (a + b) = a + b (дис-
	трибутивность2);
	Доказательство. Для доказа-
	тельства этого свойства отло-
	жим векторы a и b от точки O
	и построим на них параллело-
	грамм,диагональ которого рав-
	на их сумме(рис. 7).При“рас-
	тяжении”сторон этого паралле-
	лограмма в раз его диагональ
	в силу свойств подобия также
	“растянется”в раз.А это как
	раз и значит,что

(a + b) = a + b.

Замечание. На рис. 7показан случай > 1. 8. 1 · a = a (единица).

Доказательство. Это свойство следует из определения операции умножения вектора на число.

Определение. Множество с операциями сложения и умножения на число,удовлетворяющими данным аксиомам,называется линейным пространством.

12

Определение. Разностью векторов a и b называется вектор c такой,что c+ b = a.

Легко показать,что вектор c = a + (−1) · b является разностью векторов a и b. Действительно,

c + b = a + (−1) · b + b = a + ((−1) · b + b) = a + 0 = a.

Докажем теперь единственность такого вектора.Предположим,что вектор d также равен разности векторов a и b.Тогда с одной стороны

d + b + (−1) · b = (d + b) + (−1) · b = a + (−1) · b = c,

а с другой стороны

d + b + (−1) · b = d + (b + (−1) · b) = d + 0 = d.

Отсюда получаем,что c = d.

§7.Линейная зависимость и независимость векторов.Базис

Определение. Линейной комбинацией векторов a1, a2, . . . , an с коэффициентами

1, 2, . . . , n 2 R называется вектор вида 1a1 + 2a2 + . . . + nan .Если все j (j = 1, 2, . . . , n)равны нулю,то соответствующая линейная комбинация называется

тривиальной,в противном случае нетривиальной.

Определение. Векторы a1, a2, . . . , an называются линейно зависимыми,если существует их нетривиальная линейная комбинация,равная нулю.Иначе:найдутся такие

числа 1, 2, . . . , n ,не все из которых равны нулю,что 1a1 + 2a2 + . . . + nan = 0. В противном случае векторы линейно независимы,т.е.из равенства 1a1 + 2a2 +

. . . + nan = 0 следует,что 1 = 2 = . . . = n = 0.

Лемма1. Если среди векторов a1, a2, . . . , ak хотя бы один нулевой,то эти векторы линейно зависимы.

Доказательство. Не умаляя общности,можно считать,что a1 = 0 (мы можем перенумеровать векторы,чтобы это условие выполнялось).Рассмотрим нетривиальную линейную комбинацию

1 · a1 + 0 · a2 + . . . + 0 · ak = 0.

Лемма2. Система векторов линейно зависима тогда и только тогда,когда один из них является линейной комбинацией остальных.

Доказательство. Необходимость. Пусть имеется нетривиальная линейная комбинация векторов,равная нулю: 1a1 + 2a2 + . . . + nan = 0.Один из коэффициентов, скажем, i 6= 0.Тогда имеем

ai =

− i a1 + + −. . .

−i

1

ai−1

+

− i

ai+1 + . . . +

− i an.

1

i

i+1

n

Достаточность. Пусть ai = β1a1 + . . .

+ βi−1ai−1 + βi+1ai+1 + . . .

+ βnan .Тогда

(−1)ai + β1a1 + . . . + βi−1ai−1 + βi+1ai+1 + . . . + βnan = 0

нетривиальная,так как коэффициент при ai равен −1 6= 0.

13

Лемма3. Пусть a1, . . . , ak линейно зависимая система векторов.Тогда система векторов a1, . . . , ak, ak+1, . . . , an линейно зависимая,какими бы ни были векторы

ak+1, . . . , an .

Доказательство. Если 1a1 + . . . + kak = 0 нетривиальная линейная комбинация, то 1a1 + . . . + kak + 0 · ak+1 + . . . + 0 · an тоже нетривиальная комбинация.

Теорема7.1. Если ненулевой вектор a коллинеарен вектору b,то существует вещественное такое,что b = a.

Доказательство. Отложим векторы a = OA и b = OB от точки O.Проведем прямую,на которой лежат эти векторы.Выберем за положительное направление оси направление вектора a и выберем на оси единичный отрезок.

Если векторы OA и OB сонаправлены,положим = ||OBOA|| ,если противопо-

ложно направлены,положим = −||OBOA|| .

Тогда длины векторов b и a равны,поскольку

|OB| = | ||OA| = ||OBOA|| · |OA| = |OB|,

а направления этих векторов совпадают по определению умножения вектора на число.

Лемма4. 1) Два вектора линейно зависимы тогда и только тогда,когда они коллинеарны.

2) Три вектора линейно зависимы тогда и только тогда,когда они компланар-

ны.

3) Четыре вектора всегда линейно зависимы.

Доказательство. 1)Сразу же следует из леммы2и теоремы7.1.

2)По лемме2имеем,что c = a+ βb,откуда следует компланарность всех трех векторов,поскольку вектор c равен диагонали параллелограмма,построенного на векторе a, “растянутом”в раз и на векторе b, “растянутом”в β раз.

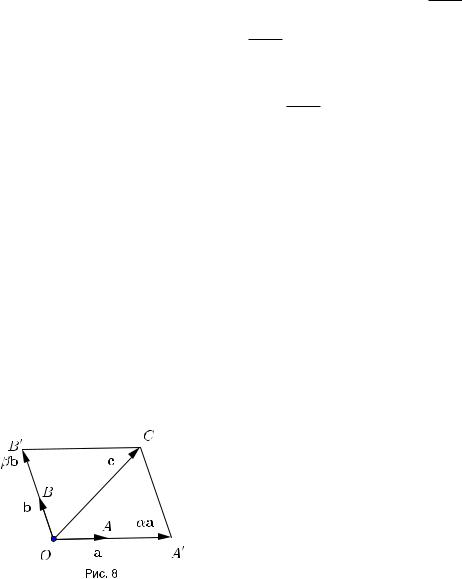
Обратно,пусть a и b коллинеарны,то есть линейно зависимы,тогда по лемме3 и векторы a, b и c линейно зависимы.Если же a и b неколлинеарны,то c можно представить в виде c = a + βb следующим образом.

Отложим все три вектора от общего начала O (рис. 8).Пусть OA = a, OB = b, OC = c.Они будут лежать в одной плоскости.Проведем через точку C прямые параллельно векторам a и b.Обозначим точки пересечения этих прямых с прямыми,на которых лежат

векторы OA и OB,соответственно через A0 и B0 . По правилу параллелограмма

c = OA0 + OB0.

Вектор OA0 коллинеарен ненулевому вектору a,следовательно, OA0 = a.Аналогично OB0 = βb.Отсюда получаем,что

c = a + βb.

3)Если три вектора компланарны,то они линейно зависимы по предыдущему пункту,и тогда все4вектора линейно зависимы по лемме3.Если же таких трех

14

векторов среди a, b, c, d нет,то пары a и b, c и d неколлинеарны,а следовательно, определяют две плоскости,которые не параллельны(иначе все4были бы компланарны).Тогда какой-либо ненулевой вектор f ,лежащий на прямой пересечения этих плоскостей,раскладывается,с одной стороны,в линейную комбинацию a и b, а с другой в линейную комбинацию c и d (см.доказательство п. 2):

a + βb = f = γc + δd.

Если при этом один из коэффициентов,скажем, ,равен нулю,то тогда векторы b, c и d компланарны,что противоречит предположению.

Таким образом,

a + βb − γc − δd = 0

нетривиальная комбинация.

Определение. Базисом на прямой(на плоскости,в пространстве)называется набор из одного(2-х, 3-х)линейно независимых векторов.

Замечание. Для прямой это означает,что вектор ненулевой.

Теорема7.2. Каждый вектор пространства(плоскости,прямой)однозначно представляется в виде линейной комбинации векторов данного базиса.

Доказательство. Докажем существование линейной комбинации.Пусть	e1 , e2 , e3
данный базис,а a произвольный вектор.По лемме4п. 3векторы	a, e1, e2, e3

линейно зависимы,так что существует нетривиальная линейная комбинация a +

1e1 + 2e2 + 3e3 = 0.Пусть = 0.Тогда 1e1 + 2e2 + 3e3 = 0 нетривиальная линейная комбинация,что противоречит линейной независимости векторов базиса.

Значит, 6= 0 и искомая комбинация

a = − 1 e1 + − 2 e2 + − 3 e3.

Докажем единственность.Пусть имеются два различных представления

a = 1e1 + 2e2 + 3e3 = β1e1 + β2e2 + β3e3.

Тогда

( 1 − β1)e1 + ( 2 − β2)e2 + ( 3 − β3)e3 = 0

нетривиальная комбинация,что противоречит линейной независимости векторов базиса.

В случае плоскости и прямой доказательство аналогично.
Определение. Координатами (или компонентами)вектора a	относительно ба-
зиса e1, e2, e3 называются такие(однозначно определенные)числа	1, 2, 3 ,что
a = 1e1 + 2e2 + 3e3 .Будем записывать также a = ( 1, 2, 3).

Лемма5. Координаты суммы векторов равны сумме координат.Координаты λa равны λ1,λ 2,λ 3 (в обозначениях определения).

Доказательство. Пусть a = 1e1 + 2e2 + 3e3 , b = β1e1 + β2e2 + β3e3 .Тогда по свойствам1, 2, 5, 6, 7

a + b = ( 1e1 + 2e2 + 3e3) + (β1e1 + β2e2 + β3e3) =

= 1e1+β1e1+ 2e2+β2e2+ 3e3+β3e3 = ( 1+β1)e1+( 2+β2)e2+( 3+β3)e3,

λa = λ( 1e1 + 2e2 + 3e3) =

= λ( 1e1) + λ( 2e2) + λ( 3e3) = (λ1)e1 + (λ2)e2 + (λ3)e3.

15

Определение. Аффинная система координат в пространстве задается выбором репера произвольной точки O и базиса e1, e2, e3 .Прямые,определяемые началом координат O и соответствующими базисными векторами,называются осями коорди-

нат.

Замечание. Слово“аффинный”происходит от латинского“a nis” смежный, соседний.

Координаты точки X относительно репера Oe1e2e3 определяются как координаты вектора OX (ее радиус-вектора)в базисе e1, e2, e3 :

OX = x1e1 + x2e2 + x3e3.

Их мы будем обозначать латинскими буквами.Записываем X(x1, x2, x3).

Лемма6. Пусть X(x1, x2, x3), Y (y1, y2, y3) координаты двух точек.Тогда координаты вектора XY относительно базиса,входящего в данную аффинную систему

координат,равны (y1 − x1, y2 − x2, y3 − x3).

Доказательство. По определению аффинной системы координат OX = (x1, x2, x3), OY = (y1, y2, y3), а XY = OY − OX.По лемме5получаем требуемый результат.

Определение. Базис называется ортогональным,если векторы e1, e2, e3 попарно перпендикулярны.Если они к тому же еще единичной длины,то базис называется ортонормированным.Аффинная система координат называется прямоугольной,если соответствующий базис ортонормирован.

Ортонормированный базис на плоскости будем обозначать i, j,в пространстве

i, j, k.

Оси координат прямоугольной системы координат имеют названия:ось Oi на-

зывается осью абсцисс,ось Oj осью ординат,ось Ok осью аппликат.Соответ-

ствующие координаты в прямоугольной системе координат называются абсциссой,

ординатой и аппликатой.

Определение. Ортом произвольного ненулевого вектора называется единичный вектор,коллинеарный исходному и имеющий то же направление,что и исходный вектор.

Рассмотрим в прямоугольной системе координат Oijk вектор OM,приведенный в общее начало с ортом e.

Определение. Косинусы углов ,β,γ ,которые образует орт e с базисными векто-

рами i, j, k,называются направляющими косинусами вектора OM.

16

ЛЕКЦИЯ3.ЦЕНТР МАСС.СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ

§8.Деление отрезка в данном отношении

Пусть заданы две точки A и B своими аффинными координатами (a1, a2, a3)

и (b1, b2, b3)					(в некотором репере)и отношение			λ	.Найдем
аффинные					координаты такой	точки		µ
							X отрезка AB ,что
	|AX|	=	λ	,то есть делящей отрезок			AB в данном отноше-
	|XB|	µ
нии.
	Обозначим через x1, x2, x3					неизвестные нам координа-
ты точки X .
	Координаты векторов AX и XB в данном базисе по
лемме6равны,соответственно,						(x1 − a1, x2 − a2, x3 − a3) и

(b1 − x1, b2 − x2, b3 − x3).По лемме5условие отношения,поскольку векторы сонаправлены,перейдет в совокупность условий

µ(x1 − a1) = λ(b1 − x1), µ(x2 − a2) = λ(b2 − x2), µ(x3 − a3) = λ(b3 − x3),

имеющих единственное решение

	xi =	µai + λbi	,	i = 1, 2, 3.	(8.1)
		µ + λ
	Заметим,что можно рассматривать и отрицательные				λ или µ,так что условие

деления в этой общей форме будет иметь вид

µAX = λXB.

Формулы ответа,будут,конечно,теми же,что и раньше.

Замечание. Данные соотношения имеют смысл для всех λ и µ,кроме случая

λ = −µ.

Пример8.5. Решим задачу о вычислении координат центра тяжести системы материальных точек.Используем следующие два допущения,соответствующих основным физическим предпосылкам:

1) Цетр тяжести двух материальных точек M1 и M2 с массами m1 и m2 соответственно находится на отрезке M1M2 и делит этот отрезок в отношении

λ = m2 .

m1

2) Центр тяжести системы материальных точек M1, M2, . . . , Mn−1, Mn с массами m1, m2, . . . , mn−1, mn соответственно совпадает с центром тяжести системы из двух точек,одна из которых является точкой Mn с массой mn ,а другая находится в центре тяжести системы материальных точек M1, . . . , Mn−1 с мас-

сами m1, . . . , mn−1 и имеет массу m1 + . . . + mn−1 .

Замечание. Вообще говоря,в физике чаще используется другое определение центра тяжести.Здесь мы рассматриваем определение,исходящее из опытноэкспериментальных данных.

17

Решение. Из первого допущения и формул(8.1)вытекает,что координаты цен-

тра тяжести двух материальных точек M1(x1, y1, z1) и M2(x2, y2, z2) равны соответственно

	m1x1 + m2x2	,	m1y1 + m2y2	и	m1z1 + m2z2	.
	m1 + m2		m1 + m2		m1 + m2

Предположим,что координаты центра тяжести системы из n материальных точек Mi(xi, yi, zi) с массами mi соответственно( i = 1, 2, . . . , n)находятся по формулам

x =

m1x1

+ . . .

+ mnxn

, y =

m1y1

+ . . .

+ mnyn

, z =

m1z1

+ . . .

+ mnzn

. (8.2)

m1 +

+ mn

m1 +

+ mn

m1 +

+ mn

Докажем наше предположение по индукции,используя второе допущение.Пусть эти формулы справедливы для системы точек M1, . . . , Mn−1 с массами m1, . . . , mn−1 соответственно.Тогда,например,для абсциссы x рассматриваемой системы точек M1, . . . , Mn получим(согласно второму допущению и формуле для двух точек):

		(m1 + . . . + mn−1) ·	m1x1+...+mn−1xn−1	+ mnxn
	x =		m1+...+mn−1		,
		(m1 + . . . + mn−1) + mn

откуда сразу же получается первая формула(8.2).Выражения для y и z получаются аналогично.

Замечание. Если система материальных точек Mi расположена в плоскости Oxy,то координаты ее центра тяжести могут быть найдены по первым двум фор-

мулам(8.2).

§9.Барицентрические координаты

Формулы(8.2)используются для введения барицентрических координат.Рассмотрим барицентрические координаты на плоскости.Пусть на плоскости введена прямоугольная система координат Oij.Рассмотрим какие-либо три различные точки M1(x1, y1), M2(x2, y2), M3(x3, y3),не лежащие на одной прямой,и произвольную данную точку M(x, y).Выясним,существуют ли такие три числа m1, m2 и m3 , удо - влетворяющие условию

m1 + m2 + m3 = 1,

(9.1)

что точка M(x, y) будет центром тяжести точек M1, M2, M3 с массами m1 , m2 , m3 соответственно.Данная задача сводится к вопросу об однозначной разрешимости системы линейных уравнений

m1 + m2 + m3 = 1,	(9.2)
m1x1 + m2x2 + m3x3 = x,

m1y1 + m2y2 + m3y3 = y.

Здесь первое уравнение это условие(9.1),а последние два уравнения следствия формул(8.2)и условия(9.1).

Рассмотрим определитель данной системы линейных уравнений

"	y1	y2	y3	"		−		− − −			− 6
"	1	1	1	"
"	x1	x2	x3	"	= (x2 x1)(y3				y1) (x3 x1)(y2		y1) = 0.
"				"
"				"
Действительно"	,определитель"					отличен от нуля,иначе получили бы пропорцию
						x2 − x1	=		y2 − y1	,
						x3 − x1		y3 − y1

18

откуда,обозначив данное отношение через −λ,получим

x1 =	x2 + λx3	, y1 =	y2 + λy3	,
	1 + λ		1 + λ
что соответствует тому,что точка M1		делит отрезок M2M3 в отношении λ (см.
формулы(8.1)),и тогда все три точки лежат на одной прямой.
Таким образом,система(9.2)однозначно разрешима относительно m1 , m2 , m3 .
Следовательно,положение любой точки		M на плоскости однозначно определяется

относительно базисных точек M1, M2, M3 этой плоскости посредством барицентрических координат m1 , m2 , m3 .

Барицентрические координаты в пространстве вводятся аналогично.Для этого используются четыре точки пространства,не лежащие в одной плоскости.

Применяются барицентрические координаты в различных химических,топологических задачах(в частности,это первые однородные координаты).Интересно их применение в колориметрии.Любой цвет может быть представлен смешением трех цветов.В1931году Международная Осветительная Комиссия(МОК)приняла в качестве основных три цвета:красныйR,зеленыйGи синийBс длинами волн соответственно λ = 700 нм, λ = 546.1 нм и λ = 435.8 нм.

При смешении цветов R, G и B можно,в частности,получить и белый цвет. Приняты различные стандарты“белизны”.Если смешать с равными интенсивностя-

ми(то есть освещенностями,скажем,по1люмену)красный цвет	R,зеленый	G и
синий B ,то получится цвет синего оттенка.В качестве стандартного белого цвета
(обозначается буквой E )принят цвет,который получается от смешения цвета		R с

освещенностью в1люмен с 4.5907 люмена цвета G и с 0.0601 люмена цвета B . Мы можем теперь наглядно изобразить цвета,получаемые от смешения трех

цветов R, G, B .Выберем на плоскости какой-нибудь треугольник и вершины его обозначим буквами R, G, B (в соответстии с основными цветами).Если некоторый цвет возник при смешении r “единиц”цвета R, g “единиц”цвета G и b “единиц”цвета B ,причем r + g + b = 1,то можно этому цвету сопоставить точку F ,имеющую 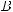барицентрические координаты (r; g; b).При этом

надо условиться,что считать“единицей”того или иного цвета.В соответствии со сказанным выше за “единицу”принимают такие интенсивности цветов R, G и B ,которые соответствуют освещенности соответственно в1, 4.6и0.06люмена.Эти координаты называют в колориметрии координатами цветности или трехцветными координатами. В

частности,стандартный белый цвет E имеет ба-

рицентрические координаты(координаты цветно-

сти) (1/3; 1/3; 1/3).

§10.Скалярное произведение

В механике и физике часто приходится иметь дело со следующей задачей:найти работу силы F,если точка,на которую действует сила,совершила перемещение OA = s.Если точка движется по направлению силы,то по определению работа силы равна произведению величины силы на длину перемещения,то есть |F| · |s|. Если же точка движется под углом ' к направлению силы,то работает только та составляющая силы F,которая направлена по линии OA,а перпендикулярная составляющая уравновешивается сопротивлением.Следовательно,работа силы будет

19

^

def

(a, b) = |a| · |b| cos(a, b).

Если один из векторов нулевой,то положим

Определение. Скалярным произведением двух(ненулевых)векторов называется число,равное произведению длин этих векторов на косинус угла между ними:

равна |F| · |s| cos '.Таким образом,по двум данным векторам F и s мы определяем скаляр.

def .

(a, b) = 0

Лемма7. Пусть в некотором ортонормированном базисе i, j, k вектор a имеет координаты (a1, a2, a3).Тогда

a1 = (a, i), a2 = (a, j), a3 = (a, k).

Доказательство. Координаты вектора могут быть найдены путем проекций в прямоугольном параллелепипеде.Так как единственность разложения по базису доказана,то

^^

a1 = |a| · cos(a, i) = |a| · |i| · cos(a, i) = (a, i).

Для остальных координат доказательство аналогично.

Теорема10.1. Скалярное произведение обладает следующими свойствами,определяющими его однозначно:

1)(a, b) = (b, a) (симметричность);

2)(a + b, c) = (a, c) + (b, c);

3)(λa, b) = λ(a, b) (2), 3) линейность по первому аргументу);

4)(a, a) = |a|2 ≥ 0,в частности, (a, a) = 0 тогда и только тогда,когда a = 0 (положительность и связь с длиной).

Доказательство. Пункты 1), 3) и 4) очевидны.Если c = 0,то пункт 2) выполяется.Если же c 6= 0,то делением на |c| с помощью п. 1) и 3) приводим утверждение к случаю |c| = 1.В этом случае рассмотрим ортонормированный базис i = c, j, k. Тогда соответствующие скалярные произведения совпадают с первыми координатами:

(a, c) = (a, i) = a1, (b, c) = (b, i) = b1.

Поскольку координаты суммы равны сумме координат,то

(a + b, c) = a1 + b1 = (a, c) + (b, c).

Покажем теперь,что свойства 1)–4) однозначно определяют значения скалярного произведения.Свойство 4) однозначно определяет значение (a, a).В силу пп. 1) и 4) имеем:

(a + b, a + b) = (a, a) + (a, b) + (b, a) + (b, b) = (a, a) + 2(a, b) + (b, b),

(a, b) = 12 [(a + b, a + b) − (a, a) − (b, b)] .

Теорема10.2. В произвольном ортонормированном базисе i, j, k скалярное произведение вычисляется по формуле

(a, b) = a1b1 + a2b2 + a3b3.

20