geometry24

ЛЕКЦИЯ10.ПОЛЯРНЫЕ УРАВНЕНИЯ КОНИК.ОБЩАЯ ТЕОРИЯ

§33.Фокальный параметр

Определение. Фокальным параметром коники,соответствующим уравнению(32.1), (32.2)или(32.3),называется число p из уравнения параболы и число

p = b2 a

для эллипса и гиперболы.

Фокальный параметр имеет простой геометрический смысл.

Определение. Фокальной осью называется ось симметрии коники,проходящая через фокус.

Фокальной хордой называется хорда(то есть отрезок,соединяющий две точки кривой),проходящая через фокус перпендикулярно фокальной оси.

Теорема33.1. Фокальный параметр p равен половине длины фокальной хорды.

Доказательство. Найдем половину длины фокальной хорды для эллипса

sb2 1 −

c2

= br

b2

b2

=

,

a2

a2

a

для гиперболы:

sb2

c2

= br

b2

b2

− 1

=

,

a2

a2

a

и для параболы:

p

r2p

= p.

2

Как видим,во всех трех случаях она равна p.

§34.Полярные уравнения коник

Выведем уравнения эллипса,гиперболы и параболы в полярных координатах. Эти уравнения используются в астрономии и механике.

Полюс полярной системы координат поместим в левый фокус эллипса(рис. 1), в правый фокус гиперболы5 (рис. 2)и в фокус параболы(рис. 3).Полярную ось направим в сторону от соответствующей(ближайшей)директрисы.

Теорема34.1. В данной полярной системе координат эллипс,парабола и правая ветвь гиперболы имеют уравнение

p

r = 1 − e cos '.

Уравнение левой ветви гиперболы следующее:

p

r = −1 + e cos '.

5Для гиперболы полярное уравнение будет определять лишь правую ее ветвь.

61

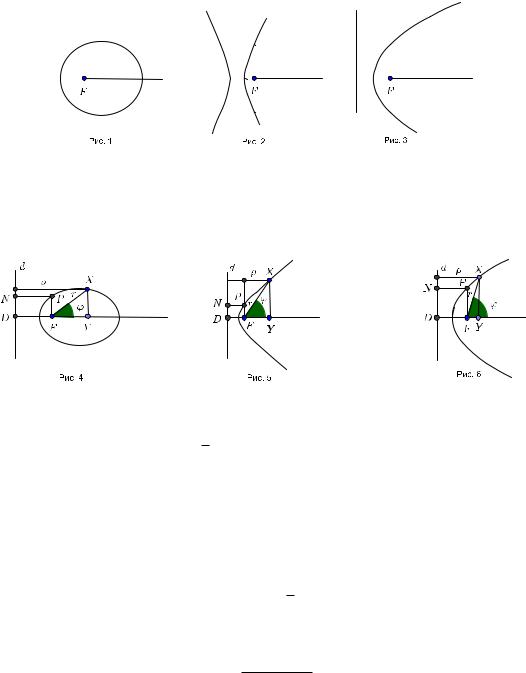
Доказательство. Рассмотрим произвольную точку X коники.Обозначим через r расстояние от нее до фокуса F (r = |XF |),а через % расстояние до директрисы d. Пусть D точка пересечения фокальной оси и директрисы, Y проекция точки X на фокальную ось, P конец фокальной хорды,а N проекция P на директрису d.Рис. 4,рис. 5и рис. 6соответствуют эллипсу,гиперболе и параболе.

Для точки X коники выполняется равенство

%r = e, или r = e%.

Очевидно,что

%= |DY | = |DF | + |F Y | = |DF | + r cos ', |DF | = |P N|,

итак как точка P это точка коники,то для нее

|P N| = pe.

Отсюда получаем,что r = p + er cos ',или

p

r = 1 − e cos '.

Для эллипса ' принимает все значения 0 ' < 2 ,для параболы ' 6= 0,для гиперболы cos ' < 1/e.

§35.Параметрические уравнения коник

Теорема35.1. Параметрические уравнения эллипса имеют вид

x = a cos t, y = b sin t, 0 t < 2 .

(35.1)

Доказательство. Для доказательства этой теоремы достаточно доказать,что си-

	стема уравнений(35.1)эквивалентна каноническому уравнению эллипса	x2	+	y2	= 1,
		a2		b2
	т.е.они имеют одно и то же множество решений.

62

Пусть сначала x = a cos t, y = b sin t.Подставим данные x и y в каноническое уравнение эллипса:

(a cos t)2 + (b sin t)2 = cos2 t + sin2 t = 1. a2 b2

Тем самым,любая точка с такими координатами x, y является точкой эллипса. Теперь рассмотрим точку эллипса,координаты которой удовлетворяют канони-

	ческому уравнению	x2		+	y2	= 1.Тогда точка с координатами (x/a, y/b) лежит на
		a2			b2
	единичной окружности			x2 + y2 = 1.Тем самым,существует такое t 2 [0, 2 ),что

x/a = cos t, y/b = sin t,и мы получаем,что любая точка эллипса может быть задана параметрическими уравнениями(35.1).

Теорема35.2. Параметрические уравнения гиперболы имеют вид
	a	1			b		1
x =		t +		, y =			t −		, t 2 R, t 6= 0.	(35.2)
	2		t		2			t

Доказательство. Опять-таки докажем,что уравнения(35.2)и каноническое урав-

нение гиперболы

x2

y2

= 1 эквивалентны.Для этого сначала перепишем канони-

−

a2

b2

ческое уравнение гиперболы следующим образом:

x

y

x

y

+

−

= 1.

(35.3)

a

b

a

b

a

1

b

1

Пусть x =

t +

, y =

t −

.Подставим эти

x и y

в уравнения(35.3),

2

t

2

t

учитывая,что

t − t · b = t,

t + t ·

a −

2 t − t

· b = t ,

2 t + t · a

+

2

2

a

1

1 b

1

1

a

1

1

b

1

1

1

получим

a + b

a − b = t · t = 1.

x

y

x

y

1

Теперь пусть кординаты точки удовлетворяют уравнению(35.3).Ясно,что

x

y

x

y

+

6= 0,

−

6= 0.

a

b

a

b

x

y

x

y

1

Положим

+

= t,

−

=

.Выражая из этих уравнений

x и y,получим

a

b

a

b

t

уравнения(35.2).

Ясно,что правой ветви гиперболы соответствуют значения параметра

t > 0, а

левой ветви гиперболы t < 0.

§36.Общая теория кривых второго порядка.Канонические уравнения

Кривые второго порядка задаются в некоторой аффинной системе координат на плоскости уравнением второй степени F (x, y) = 0,где

F (x, y) = a11x2 + 2a12xy + a22y2 + 2a1x + 2a2y + a0 =

(36.1)

63

a11	a12	x			x	+ a0
= (x, y) a12	a22	y + 2(a1		, a2)	y			= XT QX + 2LX + a0 =
		a11	a12	a1	A @	x	A	x	A
		@ a1	a2	a0		1		@ 1
= (x, y, 1) 0 a12			a22	a2	1 0 y		1 = (x, y, 1)A 0 y		1

(36.2)

(36.3)

и хотя бы один из коэффициентов aij отличен от нуля.Матрица Q размерности

	2 2 называется матрицей квадратичной части,а матрица				L размерности 1 2
	называется матрицей линейной части.
	Матрицы A и Q симметрические: AT = A, QT = Q.
	Замечание. Матрицы Q и L однозначно определяются уравнением(36.1),то
	есть если	x		x
	то A = B .		A		A
		@ 1		@ 1
	F (x, y) = (x, y, 1)A	0 y	1 = (x, y, 1)B	0 y	1 ,

Далее будем рассматривать прямоугольную систему координат,поскольку всегда можно перейти от произвольной аффинной системы координат к прямоугольной.

В дальнейшем нам понадобятся только квадратные матрицы второго и третьего порядков,но все определения распространяются на случай матриц произвольного порядка n.

Определение. Пусть M квадратная матрица n-го порядка. Собственным вектором матрицы M называется ненулевой вектор X такой,что MX = λX для некоторого λ 2 R .Число λ называется собственным числом матрицы M .

Говорят также,что собственный вектор X соответствует,или принадлежит собственному числу λ.

Замечание. Координаты векторов будем записывать по столбцам,т.е.

0 1 x1

B x C

X = B 2 C . @ . . . A

xn

Пусть X собственный вектор матрицы M ,соответствующий собственному числу λ.Рассмотрим систему линейных уравнений MX = λX .Преобразуем ее,перенеся все в левую часть: (M − λE)X = O ,где O нулевой вектор.Полученная система уравнений имеет ненулевое решение тогда и только тогда,когда определитель ее матрицы равен нулю: |M − λE| = 0.

Определение. Полином χM (λ) = det(M − λE) называется характеристическим полиномом матрицы M .

Таким образом,собственные числа матрицы M являются корнями ее характеристического полинома,а собственные векторы,принадлежащие каждому собственному числу λ,находятся из системы линейных уравнений MX = λX ,или

(M − λE)X = O .

Лемма36.1. Если X собственный вектор матрицы M ,соответствующий собственному числу λ,то для любого ненулевого числа вектор X также является собственным вектором матрицы M ,соответствующим собственному числу λ.

Доказательство.

M( X) = (MX) = (λX) = λ( X).

64

Таким образом,всегда можно выбрать собственный вектор,соответствующий данному собственному числу λ,длина которого равна единице.Для этого просто сле-

дует произвольный собственный вектор поделить на его длину,иначе говоря,взять p

вектор X0 = X/ (X, X).

Лемма36.2. Все собственные числа матрицы Q вещественные,а собственные векторы,принадлежащие различным собственным числам,ортогональны.

Доказательство. Найдем

	"		−	"
χQ(λ) =	"	a11 − λ a12		"	= λ2			(a11 + a22)λ + (a11a22		a2	).
	"	a12	a22	λ "			−		−	12
Вычислим дискриминант"			полинома"			χQ(λ):

D(χQ) = (a11 + a22)2 − 4(a11a22 − a212) = (a11 − a22)2 + 4a212 ≥ 0.

Тем самым,все собственные числа матрицы Q вещественные.Более того,они совпадают тогда и только тогда,когда a12 = 0 и a11 = a22 ,во всех остальных случаях собственные числа различны.

Пусть собственные векторы X1 и X2 принадлежат соответственно собственным числам λ1 и λ2 (λ1 6= λ2 ),т.е.

QX1 = λ1X1, QX2 = λ2X2.

Транспонируем первое равенство и учтем,что матрица Q симметрическая( QT = Q): X1T Q = λ1X1T .Рассмотрим число X1T QX2 .С одной стороны,

X1T QX2 = (X1T Q)X2 = λ1X1T X2,

а с другой

X1T QX2 = X1T (QX2) = X1T (λ2X2) = λ2X1T X2,

откуда получаем

λ1X1T X2 = λ2X1T X2, или (λ1 − λ2)X1T X2 = 0.

С учетом того,что λ1 6= λ2 ,имеем X1T X2 = (X1, X2) = 0,т.е.векторы X1 и X2 ортогональны.

Для кривых первого порядка,то есть прямых,было получено,что два уравнения F = 0 и G = 0 задают одну и ту же прямую тогда и только тогда,когда F = λG для некоторого ненулевого множителя λ.Для кривых второго порядка это не так, поскольку общее уравнение второй степени может определять и одну точку,и пустое множество точек.

Пример36.1. Мнимый эллипс задается в некоторой прямоугольной системе коор-

динат уравнением вида x2 + y2 = −1. Мнимые параллельные прямые задаются урав- a2 b2

нением y2 + a2 = 0, a 6= 0.Оба уравнения задают на вещественной плоскости пустое множество точек,но они имеют разные множества комплексных решений.

Определение. Квадрикой будем называть множество уравнений второй степени, каждое из которых получается из любого другого умножением на некоторый ненулевой множитель.

65

Так,квадрика определяется любым из уравнений F = 0, G = 0,где F = λG,

λ 6= 0.

Лемма36.3. Поворотом осей координат можно привести уравнение квадрики к виду

F 0(x0, y0) = λ1x02 + λ2y02 + 2b1x0 + 2b2y0 + b0,

где λ1, λ2 собственные числа матрицы Q.

Доказательство. Перейдем к системе координат с тем же центром O и базисом i0 = X1, j0 = X2 ,где X1 и X2 собственные векторы матрицы Q единичной длины. Если λ1 6= λ2 ,то они ортогональны,следовательно,матрица перехода C будет ортогональной и будет определять поворот.Поскольку координаты каждого вектора в старой системе координат и в новой связаны соотношением X = CX0 ,квадратичная часть в новой системе координат будет иметь вид

(CX0)T Q(CX0) = X0T (CT QC)X0 = X0T CT	λ1c11	λ2c12	X0 =
	λ1c21	λ2c22

	= X0T	λ1	0	X0 = λ1x02 + λ2y02,
		0	λ2

поскольку по столбцам матрицы C стоят собственные векторы матрицы Q. В случае же,когда λ1 = λ2 ,матрица Q уже имеет требуемый вид.

Следствие36.1. Матрица линейной части при переходе к новым координатам изменится следующим образом:

(b1, b2) = (a1, a2)C.

Кроме того, b0 = a0 .

Лемма36.4. Многочлен из леммы(36.3)параллельным переносом приводится к одному из следующих видов:

1)F 00 = λ1(x00)2 + λ2(y00)2 + , (λ1, λ2 6= 0);

2)F 00 = λ2(y00)2 + 2b1x00 , (λ2, b1 6= 0);

3)F 00 = λ2(y00)2 + , (λ2 6= 0).

Доказательство. 1) λ1, λ2 6= 0.Тогда выделяем полные квадраты

F 0(x0, y0) = λ1x02 + λ2y02 + 2b1x0 + 2b2y0 + b0 =

b1

2

b2

2

b12

b22

= λ1 x0 +

+ λ2 y0 +

+ b0

−

−

= λ1(x00)2 + λ2(y00)2 + ,

λ1

λ2

λ1

λ2

где

b1

b2

x00 = x0 +

, y00 = y0 +

λ1

λ2

формулы замены координат,обратной искомой.

2)λ1 = 0, λ2 6= 0 (если λ1 6= 0, λ2 = 0,то поменяем координаты местами). Возможны два случая:

а)если b1 6= 0, то

F 0(x0, y0) = λ2y02 + 2b1x0 + 2b2y0 + b0 =

		b2		2	b22
	= λ2 y0 +			+ 2b1x0 + b0 −		= λ2(y00)2 + 2b1x00,
		λ2			λ2

66

где

1

b0 −

b22

, y00

b2

x00 = x0 +

= y0 +

2b1

λ2

λ2

формулы замены координат,обратной искомой.

б)если b1 = 0, то

b2

2

b22

F 0(x0, y0) = λ2y02 + 2b2y0 + b0 = λ2 y0

+

+ b0 −

= λ2(y00)2 + ,

λ2

λ2

где

x00 = x0, y00 = y0 + b2

λ2

формулы замены координат,обратной искомой.Лемма доказана.

Теорема36.1. Для любой квадрики существует прямоугольная система координат,в которой она имеет один из следующих видов(называемых каноническими уравнениями данной квадрики):

	x2			y2
1)			+			= 1,			a ≥ b > 0 эллипс;
		a2			b2
	x2			y2
2)			+				= −1, a ≥ b > 0 мнимый эллипс;
		a2			b2
	x2			y2
3)			+			= 0,			a ≥ b > 0 пара пересекающихся мнимых прямых;
		a2			b2
	x2			y2
4)			−				= 1,		a > 0, b > 0 гипербола;
		a2			b2
	x2			y2
5)			−				= 0,		a ≥ b > 0 пара пересекающихся прямых;
		a2			b2
6)	y2		= 2px, (p > 0) парабола;
7)	y2		− a2			= 0,		(a > 0) пара параллельных прямых;
	2		2
8)	y		+ a			= 0,		(a > 0) пара мнимых параллельных прямых;
9)	y2		= 0 пара совпадающих прямых.

Доказательство. Рассмотрим теперь каждый из трех случаев из леммы36.4.

1) 1.Пусть λ1 и λ2 одного знака, противоположного.Переносим в правую часть и делим полученное уравнение на − :

λ1x002	+	λ2y002		= 1,
−			−

или,поскольку знак − совпадает со знаками λ1 и λ2 :

x002 y002

p 2 + p 2 = 1,

− /λ1 − /λ2

а это уравнение эллипса.

Во всех остальных случаях действуем аналогично.

2.λ1, λ2, одного знака.Получаем уравнение мнимого эллипса.

3.λ1 и λ2 одного знака, = 0.Пара мнимых пересекающихся прямых.

4.λ1 и λ2 разных знаков, 6= 0.Гипербола.

5.λ1 и λ2 разных знаков, = 0.Пара пересекающихся прямых.

2)6.парабола.

3)7. λ2 < 0.Пара параллельных прямых.

8.λ2 > 0.Пара мнимых параллельных прямых.

9.= 0.Пара совпадающих прямых.

67

Следствие36.2. Уравнение второй степени на плоскости задает одну из следующих кривых(как множество точек):эллипс;гипербола;парабола;пара пересекающихся прямых;пара параллельных прямых;пара совпадающих прямых;точка; пустое множество.

68

ЛЕКЦИЯ11.ОПРЕДЕЛЕНИЕ ВИДА И РАСПОЛОЖЕНИЯ КРИВЫХ

§37.Примеры

Приведем здесь общий алгоритм определения вида и расположения кривой второго порядка,основанный на материале лекции10,который применим также и для поверхностей.

1. Находим собственные числа матрицы Q:

det(Q

−

λE) =

"

a11 − λ

a12

λ

"

= λ2

−

Sp Qλ + det Q = (λ

−

λ1)(λ

−

λ2)

a12

a22

−

"

"

"

"

"

"

исоответствующие им собственные векторы:

(Q − λiE)	i	= O.
	βi

	Если λ1 и λ2 различны,можно	взять следующие базисные векторы:
	e10 =	( 1, β1)		, e20 =	(−β1, 1)		.
		p 12 + β12			p 12 + β12

Если же λ1 = λ2 ,изменения базиса не требуется.

2. Составляем ортогональную матрицу C = (e01, e02) и находим вид уравнений исходной кривой в базисе e01, e02) (здесь L0 = (b1, b2) = (a1, a2)C = LC, b0 = a0 ):

λ1x02 + λ2y02 + 2b1 + 2b2 + b0.

3. Выделяем полные квадраты,как это описано в лемме36.4и приводим уравнение квадрики к каноническому виду.Имеем замену координат x00 = x0 − x00, y00 =

y0 − y00 .

4. Находим координаты нового начала координат в исходной системе координат:

y0

= C y00

.

x0

x00

Тем самым,каноническая система координат имеет начало

O00(x0, y0) и базисные

векторы e10 , e20 .

Рассмотрим примеры использования данного алгоритма.

Пример37.1. Определить вид и расположение кривой

5x2 + 4xy + 8y2 − 32x − 56y + 80 = 0.

Решение. 1. Собственные числа матрицы Q:

−

−

−

"

2

8

−

λ "

−

"

5 − λ

"

det(Q λE) =

"

2

"

= λ2

13λ + 36 = (λ

4)(λ

9).

Собственные векторы" матрицы Q (достаточно"

найти собственный вектор,соот-

ветствующий λ1 = 4):

2 4 ,

2 4

β = 0 .

Q − λ1E =

1

2

1

2

0

69

Отсюда ( 1, β1) = (2, −1) и
e0 =			(2, −		1)				, e0 =					(1, 2)					.
1			p5							2				p5
2. Матрицы C и L0 имеют вид
p				p						= p5 −1 2													,
C = −1/p5 2/p5
2/ 5			1/			5						1								2 1
			1							2		1								4			82
L0 = LC = (−16, −28) · p										−1		2 =								−p		,	−p		.
				5																	5			5
Промежуточное уравнение кривой:
			8							82
4x02 + 9y02 − p							x0			− p			y0 + 80 = 0.

55

3.Выделяем полные квадраты(делаем параллельный перенос):

4

x0 − p5

2

+ 9 y0 − p5

−

5 −

5 + 80 = 0,

1

8

4

576

4x002 + 9y002 − 36 = 0,

где x0

= x00

p

p

+ 1/ 5, y0 = y00 + 8/

5.

В полученном уравнении перенесем 36 в правую часть,а затем все поделим на

36:

x002

y002

+

= 1

9

4

это каноническое уравнение эллипса.

4. Теперь найдем координаты начала новой системы координат:

y0	= C 8/p							=	3 .
						5
x0			1/p5						2
Тем самым(рис. 1),в системе координат с началом O0 = (2, 3) и базисными
векторами e10 , e20 имеем эллипс		x002		y002
			+		= 1.
	9
			4

70