geometry24

ЛЕКЦИЯ19.ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ

§65.Объекты проективной геометрии

Проективная геометрия возникла в началеXIXв.из потребностей графики и архитектуры.Уже в концеXIXв.в рамках проективной геометрии была построена теория,которая включила в единую схему геометрии Евклида,Лобачевского и Римана.

Проективная геометрия изучает некоторые особые свойства фигур,которые называются проективными.Рассмотрим произвольную фигуру A,содержащуюся в некоторой плоскости .Пусть β какая-нибудь другая плоскость и O произвольная точка пространства,не содержащаяся ни в одной из плоскостей ,β .Через точку M фигуры A и точку O проведем прямую OM ,которая пересечет плоскость β в некоторой точке M0 проекции точки M на плоскость β из центра O (рис. 1).

Проекции всех точек фигуры A образуют некоторую фигуру A0 проекцию A

на плоскость β .Операция,с помощью которой получается фигура	A0 ,называется
центральным проектированием из точки O.Варьируя выбор точки	O и плоскости

β ,можно получить бесконечное множество фигур,отчасти похожих на фигуру A, но во многих отношениях также и существенно от нее отличающихся.Так,проектируя окружность,можно получить эллипс и параболу и даже гиперболу;проектируя правильный треугольник,можно получить треугольник произвольной формы и т.д. При проектировании не сохраняются расстояния,площади и т.д.

С другой стороны,фигуры обладают свойствами,сохраняющимися при любом проектировании проективными свойствами,и с ними могут быть сопоставлены величины,также сохраняющиеся при любом проектировании.Такие свойства и величины называются инвариантами проектирования.Объектами проективной геометрии и являются инварианты проектирования.

Пример65.1. Если точки P1, P2, . . . , Pn фигуры A лежат на прямой,то проекции этих точек P10, P20, . . . , Pn0 также лежат на некоторой прямой.Таким образом,прямаяобъект проективной геометрии.

Если точки Q1, Q2, . . . , Qn фигуры A лежат на каком-либо коническом сечении k,то проекции этих точек Q01, Q02, . . . , Q0n также лежат на некотором коническом сечении k0 .Коническое сечение есть объект проективной геометрии.Здесь важно, что свойства,присущие исключительно эллипсу,или гиперболе,или параболе,не

121

сохраняются,поэтому в проективной геометрии не делается различия между этими кривыми,как в элементарной геометрии.

В проективной геометрии употребляются бесконечно удаленные элементы. Пусть A произвольная точка пространства и a прямая,не проходящая

через точку A.Проведем через A и a плоскость и рассмотрим пучок прямых в плоскости с центром в точке A.

Каждой точке M прямой a сопоставим тот луч6 m пучка,который пересекает a в точке M .Луч m называется лучом,проектирующим точку M .Таким образом,установлено соответствие,называемое перспективным соответствием,между точками прямой a и лучами пучка с центром в A (рис. 2).

Однако не любому лучу пучка соответствует точка прямой a.Именно,луч a0 пучка,параллельный прямой a,не пересекает ее и поэтому не имеет соответствующей себе точки.Таким образом,соответствие между лучами пучка с центром в A и точками прямой a не является взаимно однозначным.Чтобы избежать неудобств, возникающих из-за этого при исследовании проектирований, уславливаются рассматривать параллельные прямые как пере-

секающиеся на бесконечности.Тогда луч a0 в пучке с центром

в A,параллельный прямой a,как и всякий другой луч пучка,

будет иметь на прямой a соответствующую себе точку,но толь-

ко не обыкновенную точку,а некоторый новый объект,назы-

ваемый бесконечно удаленной,или несобственной точкой пря-

мой a.

Бесконечно удаленная точка прямой считается принадлежащей также любой плоскости,проходящей через эту прямую.Далее,полагают,что параллельные прямые имеют одну общую бесконечно удаленную точку.Поэтому систему параллельных прямых,расположенных в одной плоскости,называют пучком с бесконечно удален-

ным центром или несобственным пучком.

Несобственный пучок при проектировании может перейти в обыкновенный пу-

чок.

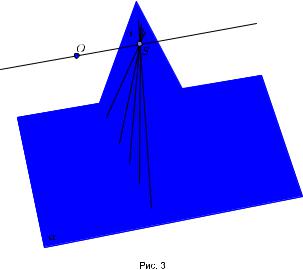
Несобственный пучок в плоскости проектируется из центра O на плоскость β в обыкновенный пучок с центром в S (рис. 3).

Бесконечно удаленные точки непараллельных прямых считаются различными. Таким образом,каждая плоскость содержит бесконечно много различных бесконечно удаленных точек.Совокупность всех бесконечно удаленных точек плоскости назы-

вают бесконечно удаленной,или несобственной прямой.

Совокупность всех бесконечно удаленных точек пространства называют беско-

нечно удаленной,или несобственной плоскостью.

Действительно,две параллельные плоскости имеют общие бесконечно удаленные точки,поэтому совокупность бесконечно удаленных точек плоскости можно рассматривать как пересечение двух параллельных плоскостей.Поэтому совокупность бесконечно удаленных точек плоскости естественно назвать прямой.

Множество всех бесконечно удаленных точек пространства при пересечении с любой обыкновенной плоскостью определяет бесконечно удаленную прямую.Поэтому это множество естественно назвать плоскостью.

6Название объясняется тем,что прямые удобно представлять себе как лучи,посылаемые во все стороны источником света,расположенным в точке A,однако следует помнить,что луч пучка есть полная прямая,а не полупрямая.

122

Прямая,дополненная бесконечно удаленной точкой,называется проективной прямой (ее следует представлять себе как замкнутую линию).Плоскость,дополненная бесконечно удаленной прямой,называется проективной плоскостью.Пространство,дополненное бесконечно удаленной плоскостью,называется проективным про-

странством.

Замечание. Бесконечно удаленные объекты вводятся в рассмотрение и в элементарной геометрии.Однако использование их по существу ограничивается лишь особой манерой изложения геометрических фактов(параллельные прямые называют сходящимися в бесконечности,цилиндр рассматривают как конус с бесконечно удаленной вершиной и т.д.).В проективной геометрии бесконечно удаленные элементы играют такую же роль,как и обыкновенные.Элементарная геометрия в значительной степени посвящена изучению метрических свойств фигур,т.е.свойств,связанных с измерением геометрических величин(длин,углов и площадей).Измерение любого отрезка AB с обыкновенными концами всегда возможно и приводит к некоторому числу,выражающему длину отрезка AB .Однако в том случае,когда один конец отрезка является бесконечно удаленной точкой,процесс измерения теряет смысл,так как на таком отрезке линейная единица откладывается бесконечно много раз.Так же невозможно измерение углов,одна сторона которых является бесконечно удаленной прямой и т.д.Таким образом,в элементарной геометрии бесконечно удаленные элементы играют особую роль и существенно отличаются от обыкновенных элементов. В проективной же геометрии,поскольку метрические свойства элементов не являются ее объектами,исчезает отличие бесконечно удаленных элементов от остальных. Более того,поскольку при проектировании бесконечно удаленные элементы могут переходить в обыкновенные,то они не обладают никакими отличными проективными свойствами.В проективной геометрии различия между обыкновенными и бесконечно удаленными элементами нет!

§66.Связка как модель проективной плоскости

Мы рассмотрели пучок прямых как модель проективной прямой.Аналогично моделью проективной плоскости может быть связка.

Определение. Точка называется инцидентной прямой,если точка лежит на этой прямой.Прямая называется инцидентной точке,если прямая проходит через эту

123

точку.

Определение. Связкой прямых и плоскостей с центром O в трехмерном пространстве называется множество всех прямых и плоскостей,проходящих через данную точку O.Обозначаться связка будет все той же буквой O.Прямая связки инцидентна плоскости,если она в ней содержится.Плоскость связки инцидентна прямой,если она через нее проходит.

Определение. Перспективное соответствие осуществляет взаимно-однозначное соответствие пополненной плоскости и связки,то есть отображение точек пополненной плоскости на множество прямых

связки,определяемое следующим образом.Рассмотрим пополняемую плоскостькак лежащую в трехмерном простран-

стве.Пусть точка O не принадлежит и определяет связку.Каждой собственной точке поставим в соответствие единственную прямую связки,проходящую че-

рез нее.Каждой несобственной точке ,

то есть направлению или несобственному пучку на ,поставим в соответствие единственную прямую связки,имеющую то же

направление(параллельную прямую,проходящую через O).

Очевидно,что выполнены следующие условия.

Утверждение. При перспективном соответствии прямые переходят в плоскости и сохраняется отношение инцидентности.Поэтому прямые связки называют“точками”,а плоскости “прямыми”данной модели проективной плоскости.

Замечание. При перспективном соответствии несобственная прямая переходит в плоскость связки,параллельную .Таким образом,пополненная плоскость соответствует связке с выделенной плоскостью,а проективная плоскость просто связке.

§67.Однородные координаты точек на плоскости и лучей в связке

Определение. Пусть на плоскости задана система аффинных координат oe1e2 (начало ее будем обозначать строчной буквой o).Пусть M произвольная точка плоскости, (x, y) ее координаты в системе oe1e2 .Тогда всякая тройка чисел x1, x2, x3 ,пропорциональная тройке x, y, 1,называется тройкой однородных координат точки M (определенных данной аффинной координатной системой oe1e2 ).

Чтобы по данной тройке x1, x2, x3 однородных координат точки M найти ее аффинные координаты,нужно найти ту тройку x, y, 1,которой тройка x1, x2, x3 пропорциональна.Для этого нужно решить пропорцию

x : y : 1 = x1 : x2 : x3,

откуда x = x1/x3 , y = x2/x3 .

Таким образом,каждая точка M плоскости получила бесконечное множество однородных координат.Множество всех троек однородных координат какойлибо точки плоскости есть класс пропорциональных троек,в который не входит “запрещенная тройка” тройка,состоящая из трех нулей,так как она не может

124

быть пропорциональна никакой тройке x, y, 1.Также никакой класс“особых троек”троек вида x, y, 0 не может являться однородными координатами никакой точки плоскости.Выясним геометрический смысл однородных координат.

Снова рассмотрим связку с центром O.Возьмем произвольную аффинную систему координат в пространстве с началом в точке O.Координаты какого-либо вектора в этой системе координат будем обозначать x1, x2, x3 .

Определение. Для произвольного луча связки координаты любого направляющего вектора этого луча x1, x2, x3 будем называть тройкой однородных координат данного луча в аффинной системе координат Oe1e2e3 .

Каждый луч имеет бесконечно много троек однородных координат,среди которых нет“запрещенной тройки” 0, 0, 0,так как нулевой вектор не может быть направляющим вектором луча.Любая тройка,отличная от“запрещенной”,очевидно,является тройкой однородных координат некоторого луча.Очевидно,что особые тройки вида x1, x2, 0 соответствуют в качестве координат тем и только тем лучам,которые лежат в плоскости Oe1e2 .

Определение. Пусть дана плоскость с системой аффинных координат oe1e2 на ней.Возьмем аффинную систему координат Oe1e2e3 в пространстве с началом O 6= o,теми же двумя векторами e1 и e2 и третьим вектором Oo.Такая система координат Oe1e2e3 называется естественно связанной с системой oe1e2 в плоско-

сти .

В системе координат Oe1e2e3 плоскость очевидно имеет уравнение x3 = 1

(рис. 5).

Тройки однородных координат какой-либо точки M плоскости это тройки однородных координат перспективного к этой точке луча связки(если аффинная система координат Oe1e2e3 естественно связана с си- 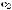стемой oe1e2 ).Так как классы особых троек

это классы однородных координат лучей связ-

ки,параллельных плоскости ,и именно этим

лучам и должны соответствовать несобствен-

ные точки плоскости ,то естественно считать

особые тройки тройками однородных координат несобственных точек плоскости.Таким образом,множество всех классов числовых троек поставлено во взаимно однозначное соответствие с множеством всех точек плоскости.

Обозначение. Точку M с однородными координатами x1, x2, x3	будем записы-
вать M = (x1 : x2 : x3).
§68.Уравнение прямой на плоскости в однородных координатах
Пусть на плоскости задана прямая d уравнением
a1x + a2y + a3 = 0	(68.1)

в системе координат oe1e2 .Пусть точка M(x, y) какая-либо точка прямой d и x1, x2, x3 некоторая тройка ее однородных координат.Выразим аффинные координаты точки M через ее однородные координаты и подставим полученные значения

вуравнение прямой,получим

x= x1 , y = x2 , a1 x1 + a2 x2 + a3 = 0, x3 x3 x3 x3

125

т.е.	(68.2)
a1x1 + a2x2 + a3x3 = 0.

Это и есть уравнение прямой d в однородных координатах.

Если какая-то тройка однородных координат точки M удовлетворяет уравне-

нию(68.2),то очевидно,что и любая тройка однородных координат точки	M пря-
мой удовлетворяет этому уравнению,в частности,ему удовлетворяет и тройка	x, y, 1,

где x и y аффинные координаты точки M .Значит,аффинные координаты x, y удовлетворяют уравнению(68.1),и точка M лежит на прямой d.

Однако на проективной плоскости имеется и несобственная точка,притом только одна,координаты которой удовлетворяют уравнению(68.2).В самом деле,если x1, x2, 0 тройка координат несобственной точки,удовлетворяющей уравнению(68.2),то a1x1 + a2x2 = 0,откуда x1 : x2 = −a2 : a1 ,и единственная несобственная точка,удовлетворяющая уравнению(68.2),есть точка (−a2 : a1 : 0).Тройки

координат этого класса и только они это тройки координат единственного несобственного луча,лежащего в плоскости Od.Так как при перспективном соответствии между связкой O и плоскостью ¯ отношение инцидентности сохраняется,то точка (−a2 : a1 : 0) инцидентна прямой d,и она единственная несобственная точка прямой d (в направлении которой точка и ушла в бесконечность).

Как и следовало ожидать,две прямые имеют общую несобственную точку тогда

итолько тогда,когда они параллельны.

Вслучае,когда в уравнении(68.2) a1 = a2 = 0, a3 6= 0,т.е.оно имеет вид

a3x3 = 0 , x3 = 0,

ему удовлетворяют все несобственные точки плоскости и только они.Это уравнение первой степени,его естественно считать уравнением несобственной прямой плоскости.

§69.Координаты прямой

Пусть на проективной плоскости ¯ дана прямая

a1x1 + a2x2 + a3x3 = 0.

Тройка коэффициентов a1, a2, a3 вполне определяет это уравнение и,следовательно, прямую,выражаемую этим уравнением.При этом два уравнения a1x1 +a2x2 +a3x3 = 0 и b1x1 + b2x2 + b3x3 = 0 задают одну и ту же прямую тогда и только тогда,когда их коэффициенты пропорциональны между собой,то есть a1 : b1 = a2 : b2 = a3 : b3 .

Определение. Тройка коэффициентов a1, a2, a3 уравнения прямой d называется тройкой(однородных)координат данной прямой,а также тройкой координат плоскости Od связки O (в системе координат Oe1e2e3 ,естественно связанной с системой oe1e2 в плоскости .

Очевидно,что множество всех координат данной прямой есть класс троек. Всякая незапрещенная тройка чисел может рассматриваться и как тройка коор-

динат точки на проективной плоскости,и как тройка координат некоторой прямой. Две тройки определяют при этом одну и ту же точку(соответственно одну и ту же прямую),тогда и только тогда,когда они пропорциональны между собою.

Обозначение. Прямую с координатами u1, u2, u3 будем обозначать как {u1 : u2 : u3}.

126

Прямая {u1 : u2 : u3} и точка (x1 : x2 : x3) инцидентны,если u1x1 + u2x2 + u3x3 = 0.

Пример69.1. Прямая y = x или x1 − x2 = 0 есть прямая {1 : −1 : 0}.Прямая

y = 1 или x2 − x3 = 0 есть прямая {0 : 1 : −1}.Прямая x = 0 (ось ординат)или x1 = 0 есть прямая {1 : 0 : 0}.Несобственная прямая x3 = 0 есть прямая {0 : 0 : 1}.

127

ЛЕКЦИЯ20.ПРИНЦИП ДВОЙСТВЕННОСТИ

§70.Принцип двойственности для проективной плоскости

Дадим сначала общее определение проективной плоскости.

Определение. Проективной плоскостью называется множество P ,состоящее из элементов двух родов,называемых соответственно“точками”и“прямыми”,связанными между собой некоторым отношением,называемым“отношением инцидентности” между какой-нибудь“точкой”и какой-нибудь“прямой” (это значит,что относительно каждой“точки”и каждой“прямой”известно,инцидентны они между собой или нет). При этом требуется,чтобы существовало взаимно однозначное соответствие между “точками”и“прямыми”проективной плоскости P с одной стороны,и прямыми и плоскостями связки,с другой стороны: “точка”и“прямая”проективной плоскости

P инцидентны между собой тогда и только тогда,когда инцидентны соответствующие им прямая и плоскость связки.В частности,проективной плоскостью является и сама связка,если ее прямые называть“точками”,а плоскости “прямыми”.

Вернемся к условию инцидентности

u1x1 + u2x2 + u3x3 = 0.

(70.1)

Поставим в соответствие каждой точке (x1 : x2 : x3) проективной плоскости прямую {x1 : x2 : x3} с теми же координатами и наоборот,прямой {u1 : u2 : u3} поставим в соответствие точку (u1 : u2 : u3),т.е.сделаем взаимно однозначное отображение множества всех элементов(точек и прямых)проективной плоскости на себя, записывающееся в виде

(x1 : x2 : x3) $ {x1 : x2 : x3}.

(70.2)

Отображение(70.2)сохраняет отношение инцидентности,т.е.переводит точку

(x1 : x2 : x3) и прямую {u1, u2, u3},инцидентные между собой,в прямую {x1 : x2 : x3} и точку (u1 : u2 : u3),по-прежнему инцидентные между собой.

Непосредственным следствием этого факта является следующий Принцип двойственности. Если верно некоторое общее утверждение о точ-

ках,прямых и инцидентности между ними на проективной плоскости,то верно и двойственное утверждение,в котором точки и прямые меняются местами.

Приведем пример двойственных теорем.

Теорема70.1. Ко всяким двум различным точкам A, B имеется единственная прямая,им инцидентная прямая (AB).

Теорема70.2. Ко всяким двум различным прямым a, b имеется единственная точка,им инцидентная точка a · b.

Замечание. Другими словами теорему70.1можно сформулировать так:через всякие две различные точки проходит одна и только одна прямая.Теорема70.2: всякие две различные прямые пересекаются в одной точке(собственной или несобственной между ними на проективной плоскости различий нет!).

Приведем доказательство только первой теоремы.Доказательство второй получится из него простой заменой“точек”на“прямые”и обратно.

128

Доказательство. Пусть (a1 : a2 : a3) и (b1 : b2 : b3) две данные различные точки. Найдем все возможные прямые { 1 : 2 : 3},инцидентные двум данным точкам. Искомые прямые удовлетворяют условиям

a1 1 + a2 2 + a3 3 = 0,

b1 1 + b2 2 + b3 3 = 0,

откуда

"

"

"

"

"

"

a2

a3

a3

a1

a1

a2

1

: 2 : 3

=

"

"

:

"

"

:

"

"

,

(70.3)

"

b2

b3

"

"

b3

b1

"

"

b1

b2

"

"

"

"

"

"

"

т.е.координаты 1, 2, 3 определены с точностью до постоянного множителя однозначно.Таким образом,прямая,инцидентная двум данным точкам,единственная.

Тогда уравнение искомой прямой имеет вид

1x1 + 2x2 + 3x3 = 0,						(70.4)
где 1, 2, 3 определяются предыдущей пропорцией,и его можно записать в виде
"	x1	x2	x3	"
"	a1	a2	a3	"		(70.5)
"				" = 0.
"				"		{
"	b1	b2	b3	"
Этому уравнению удовлетворяют"координаты"всех точек,инцидентных прямой							1 :
2 : 3}.
Первая строка матрицы					1
		x1 x2 x3
	0 a1		a2	a3
	@ b1		b2	b3	A

есть линейная комбинация остальных двух строк,т.е.

x1	= λa1		+ µb1
x2	=	λa2	+ µb2	(70.6)
x3	=	λa3	+ µb3.

Придавая параметрам λ и µ всевозможные значения(кроме запрещенной пары значений λ = µ = 0),по формулам(82.1)будем получать тройки однородных координат всевозможных точек M прямой AB .При этом очевидно,что двум пропорциональным парам λ0 : µ0 = λ00 : µ00 будут соответствовать пропорциональные тройки координат x01 : x02 : x03 = x001 : x002 : x003 .Обратно,пусть формулы(82.1)определяют для данных значений λ0, µ0 и λ00, µ00 одну точку,т.е.две пропорциональные тройки x01, x02, x03 и x001, x002, x003 ,тогда x01 = kx001, x02 = kx002, x03 = kx003 и

λ0a1 + µ0b1 = k(λ00a1 + µ00b1), λ0a2 + µ0b2 = k(λ00a2 + µ00b2), λ0a3 + µ0b3 = k(λ00a3 + µ00b3),

т.е.

(λ0 − kλ00)a1 = (kµ00 − µ0)b1, (λ0 − kλ00)a2 = (kµ00 − µ0)b2, (λ0 − kλ00)a3 = (kµ00 − µ0)b3,

откуда следует,что или λ0 = kλ00, µ0 = kµ00 ,или тройки a1, a2, a3 , b1, b2, b3 пропорциональны,что противоречит тому,что точки A и B различны.Итак,точки прямой { 1 : 2 : 3} взаимно однозначно соответствуют классам пропорциональных пар значений параметров λ, µ.

129

Определение. Уравнения(82.1)называются	параметрическими уравнениями пря-
мой AB .
Если же {a1 : a2 : a3} и {b1 : b2 : b3} две различные прямые,то уравне-
ние(70.3)определяет их точку пересечения	( 1 : 2 : 3).Уравнение(70.5)или(70.4)

есть уравнение(относительно x1, x2, x3 ),которому удовлетворяет любая тройка ко-

ординат всякой прямой d = {x1 : x2 : x3},инцидентной точке a · b = ( 1 : 2 : 3),т.е. это уравнения пучка прямых с центром a · b.Уравнения(82.1) это система пара-

метрических уравнений этого пучка.Они выражают тот факт,что каждая прямая пучка есть линейная комбинация каких-либо двух прямых этого пучка.

Следствие70.1. Равенство (70.5) является необходимым и достаточным услови-

ем того,что три точки (x1 : x2 : x3), (a1 : a2 : a3), (b1 : b2 : b3) инцидентны одной и той же прямой.

Естественно,справедливо и двойственное утверждение:

Следствие70.2. Равенство (70.5) является необходимым и достаточным услови-

ем того,что три прямые {x1 : x2 : x3}, {a1 : a2 : a3}, {b1 : b2 : b3} инцидентны одной и той же точке.

Теорема70.3.Дезарга 7. Пусть на проективной плоскости заданы два треугольника ABC и A0B0C0 ,причем одноименные вершины и стороны,точнее,прямые, их содержащие,не совпадают.Тогда три прямые AA0 , BB0 и CC0 пересекаются в одной точке в том и только в том случае,если точки пересечения прямых AB и A0B0 , AC и A0C0 , BC и B0C0 лежат на одной прямой.

Доказательство.	Обозначим указанные точки пересечения через P, Q и R (рис.
1).
Доказательство необходимости. Пусть S точка пересечения прямых AA0 ,
BB0 и CC0 .Пусть	a, b, c, a0, b0, c0, p, q, r, s некоторые представлители(тройки)од-

нородных координат точек A, B, C, A0, B0, C0, P, Q, R, S : a = (a1 : a2 : a3), . . . Тогда

7Дезарг(1593–1662) выдающийся французский геометр,один из основателей проективной геометрии

130