geometry24

Рассмотрим механический смысл кривизны.Для натуральной параметризации

r00 = dsdt = kn.Рассмотрим кривую как траекторию движения точки единичной массы

в силовом поле.Тогда вектор ускорения

r00

равен действующей на точку силе.Имеем

d2r

d2r

ds

2

dr d2s

ds

2

d2s

a =

=

·

+

·

= k(s) ·

n +

t,

dt2

ds2

dt

ds

dt2

dt

dt2

d2r

d2r

ds

2

ds

2

, n =

, n

= (kn, n)

= kv2.

dt2

ds2

dt

dt

Кривизна пропорциональна абсолютной величине нормальной составляющей силы и обратно пропорциональна квадрату линейной скорости.Чем больше сила,тем более она искривляет движение,но это влияние тем меньше,чем движение быстрее.

Теорема90.2. Если r = r(t) регулярная параметризация кривой γ ,то для квадрата кривизны этой кривой справедлива формула

k2 = [r0, r00]2 .

(r02)3

Доказательство. Выразим вторую производную вектор-функции r по дуге s через производные по t.Имеем

r0 = r0ss0.

Отсюда

r02 = s02.

Следовательно,

r0

rs0

=

p

.

r02

Дифференцируя это равенство еще раз по t,получаем

r00

p

r0

· 2(r0, r00)

r0

2

−

r00r0

2

− (r0,

r00)r0

s0 =

2p

=

.

r00

r02

ss

r02

r02pr02

Возводя это равенство в квадрат,будем иметь

r002

·

s02

=

r002r04 + (r0, r00)2r02 − 2r02(r0, r00)2

=

r002r02 − (r0, r00)2

.

ss

r06

r04

Теперь заметим,что

s02 = r02 :

k2 = r002r02 − (r0r00)2 ,

(r02)3

или,что то же самое

k2 = [r0, r00]2 .

(r02)3

Пользуясь определениями и свойствами скалярного,двойного векторного и смешанного произведений векторов,докажем равенство

[r0, r00]2 = r002r02 − (r0r00)2.

[r0, r00]2 = ([r0, r00], [r0, r00]) = (r0, r00, [r0, r00]) = −(r0, [r0, r00], r00) =

= −([r0, [r0, r00]], r00) = −(r0(r0, r00) − r00(r0, r0), r00) = r02r002 − (r0, r00)2.

171

Отсюда для кривизны кривой,заданной уравнениями

x = x(t), y = y(t), z = z(t),

получаем

"

"

2

2"

"

2

"

"

2

k

=

x

y

y

z

z

x

x000

y000

+

y000

2

2 3

z000

x000

.

2

"

"

"

z000

"

+

"

"

"

"

(x0

"

+ y0

+

"z0

)

"

"

"

"

"

"

"

"

Если кривая плоская и расположена в плоскости xy, то

k2 = (x00y0 − x0y00)2 .

(x02 + y02)3

Если плоская кривая задана уравнением y = y(x), то

y002

k2 = (1 + y02)3 .

Найдем кривизну кривой,заданной уравнением в полярных координатах. Пусть кривая задана уравнением r = r(').Подставим в формулы,выражающие

прямоугольные координаты через полярные

x = r cos ', y = r sin '

выражение r через ',получим

x = r(') cos ', y = r(') sin '.

Данные уравнение можно рассматривать как параметрические уравнения кривой( 'параметр).Тогда

ddx' = ddr' cos ' − r sin ', ddy' = ddr' sin ' + r cos ',

d2x		d2r		dr		d2y		d2r		dr
	=		cos ' − 2		sin ' − r cos ',		=		sin ' + 2		cos ' − r sin '.
d'2		d'2		d'		d'2		d'2		d'

Полученные выражения подставим в формулу для кривизны и получим ее значение:

|r2 + 2r02 − rr00| k = (r2 + r02)3/2 .

Замечание. Кривизна кривой по определению неотрицательна.Для плоских кривых во многих случаях имеет смысл рассматривать кривизну со знаком,считая ее в одних случаях положительной,в других отрица- тельной.При этом пользуются следующим соображени-

ем.Касательный вектор r0(t) кривой при движении вдоль кривой в направлении возрастающих t поворачивается.В зависимости от направления вращения вектора r0(t) кри-

визну считают положительной или отрицательной.

Если определить этим условием знак кривизны плоской кривой,то для нее получается формула

172

x00y0

−

x00y0

или k =

−

x00y0

−

x00y0

k =

3

3

.

(x02 + y02)

2

(x02 + y02)

2

В частности,для задания кривой уравнением

y = y(x)

k =

y00

или k = −

y00

.

(1 + y02)23

(1 + y02)23

Найдем теперь все кривые,имеющие в каждой точке кривизну,равную нулю.

Имеем

k = |r00(s)| = 0.

Отсюда r00(s) = 0 и r(s) = as + b,где

a и b постоянные векторы.

Таким образом,кривая,имеющая всюду кривизну,равную нулю,является либо прямой,либо открытым отрезком прямой.Обратное также верно.

Кривизна есть мера отклонения кривой от прямой линии,кривизна которой равна нулю.

§91.Кручение кривой

Пусть P произвольная точка кривой γ и Q точка кривой,близкая к P . Обозначим угол между соприкасающимися плоскостями кривой в точках P и Q, а s длину отрезка P Q кривой.

Определение. Абсолютным кручением | | кривой γ в точке P называется предел отношения s при Q ! P .

Теорема91.1. Регулярная(трижды непрерывно дифференцируемая)кривая в каждой точке,где кривизна отлична от нуля,имеет определенное абсолютное кручение | |.Если r = r(s) естественная параметризация кривой,то

|

|

=

|(r0, r00, r000)|.

k2

Доказательство. Если кривизна кривой γ в точке P отлична от нуля,то по непре-

рывности она отлична от нуля в точках,близких к

P .В каждой точке,где кривизна

отлична от нуля,векторы r0

и r00 отличны от нуля и не параллельны.Поэтому в каж-

дой точке Q,близкой к

P ,существует определенная соприкасающаяся плоскость.

Пусть b(s) и b(s+

s) единичные векторы бинормали в точках P и Q кривой

γ .Угол равен углу между векторами b(s) и b(s +

s).

Так как

векторы b(s) и b(s + s) единичные и образуют угол ,то b(s +

|

s) − b(s)| = sin

2 .Поэтому

= 2 sin 2

2

|b(s +

s) − b(s)|

= sin

.

s

s

·

s

2

173

[r0, r00]2

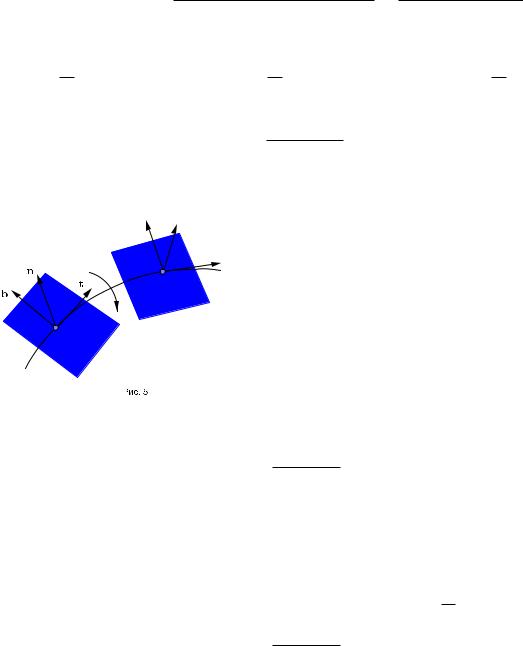
Отсюда,переходя к пределу при

s ! 0,получаем

| | = |b0|.

Вектор b0

перпендикулярен b,так как bb0

= 1 (b2)0

= 0.Также он перпендику-

лярен и t.Действительно,

2

b0 = [t, n]0 = [t0, n] + [t, n0].

но t0kn,поэтому

b0 = [t, n0],откуда следует,что

b0 перпендикулярен t.Таким об-

разом,вектор

b0

параллелен вектору n,и,следовательно,

| | = |(b0, n)|.

Подставим сюда n = 1 r00 и b =

[r0,r00]

,для чего сначала найдем b0 :

k

k

b0 =

[r0

, r00]

0 =

k([r00, r00] + [r0, r000]) − k0[r0, r00]

=

k[r0, r000] − k0[r0, r00]

.

k

k2

k2

Теперь воспользуемся полученным равенством:

|(b0, n)| = k13 ·|(k[r0, r000]−k0[r0, r00], r00)| = k13 ·|k(r0, r000, r00)−k0(r0, r00, r00)| = k12 |(r0, r00, r000)|.

Таким образом,

| | = |(r0, r00, r000)|.

k2

Определим теперь кручение кривой.

Из параллельности векторов b0 и n следует,что при движении вдоль кривой в сторону возрастающих s соприкасающаяся плоскость кривой поворачивается около касательной к кривой.В связи с этим кручение кривой определяется равенством

= ±| |

и знак (+),если вращение касательной плоскости происходит в направлении от b к n, и (−), если вращение происходит в направлении от n

к b.

Определив так кручение кривой,будем иметь = (b0, n) или

= −(r0, r00, r000).

k2

Найдем выражение для кручения кривой в случае любой регулярной параметризации r = r(t).Имеем

r0s = r0t0, r00ss = r00(t0)2 + r0t00, r000sss = r000(t0)3 + {r0, r00},

где {r0, r00} линейная комбинация векторов r0 и r00 .Подставляя найденные выражения для r0s , r00ss и r000sss в формулу для и замечая,что t02 = r102 ,получим

= −(r0, r00, r000).

174

Найдем теперь все кривые,у которых в каждой точке кручение равно нулю. Имеем

= (b0, n) = 0.

Так как,кроме того (b0, t) = 0 и (b0, b) = 0, то b0 = 0, b = b0 = const.

Векторы t и b перпендикулярны.Поэтому (r0, b0) = 0.Отсюда (r, b0)0 = 0. Следовательно, (r, b0) = const,т.е.радиус-вектор любой точки кривой удовлетворяет уравнению плоскости.В этой плоскости и лежит кривая.

Итак,кривая,у которой кручение в каждой точке равно нулю,плоская.Обратное тоже верно.

Тем самым,кручение кривой характеризует ее отличие от плоской кривой.

175

ЛЕКЦИЯ27.ФОРМУЛЫ ФРЕНЕ.ЭВОЛЮТА

§92.Формулы Френе.Натуральные уравнения кривой

Три луча,исходящие из точки кривой и имеющие направления векторов t, n, b, являются ребрами трехгранного угла.

Определение. Этот трехгранный угол называется естественным трехгранником.

При исследовании свойств кривой в окрестности произвольной точки P во многих случаях оказывается удобным выбрать прямоугольную систему координат,приняв точку P кривой за начало координат,а оси естественного трехгранника за оси координат.Далее получим уравнение кривой при таком выборе системы координат.

Выразим производные векторов t, n, b по дуге кривой через сами векторы t, n, b. Имеем

t0 = r00 = kn.

Вектор b0 параллелен n и b0n = .Отсюда

b0 = n.

Наконец

n0 = [b, t]0 = [b0, t] + [b, t0] = [ n, t] + [kb, n] = −(kt + b).

Формулы

t0	=	kn
n0	= −kt− b,
b0	=	n

называются формулами Френе8.

Найдем разложение радиус-вектора r(s+ s) в окрестности произвольной точки P ,соответствующей дуге s,по осям естественного трехгранника в этой точке.Имеем

s2

s3

r(s +

s) = r(s) +

sr0 +

r00 +

r000 + . . .

6

2

Но в точке 0 r = 0, r0 = t, r00 = kn,

r000 = k0n − k2t − k b, . . . и т.д.Таким образом,

r(s + s) =

s −

k2 s3

+ . . . t +

k s2

+

k0

s3

+ . . . n+

6

2

6

+ −

k s3

+ . . . b.

6

Отсюда,принимая касательную,главную нормаль и бинормаль за оси x, y, z прямоугольной системы координат,получаем уравнение кривой,отнесенное к осям естественного трехгранника

x =		s −			k2 s3			+ . . . ,
				6
y =	k s2			+			k0	s3	+ . . . ,
		2		6
z = −		k			s3
						+ . . .
		6

8Жан Фредерик Френе(1816–1900) французский математик,астроном и метеоролог.

176

Проекции кривой на плоскости естественного трехгранника в окрестности его вершины задаются соответствующими парами этих уравнений.Вид проекций при k, 6= 0 показан на рисунке.

Для дальнейшего нам понадобится теорема из курса дифференциальных уравнений.

Теорема92.1. Рассмотрим систему линейных дифференциальных уравнений

	dy1	= a11y1 + a12y2 + . . . + a1nyn + f1,
	dx
	dy2	= a21y1 + a22y2 + . . . + a2nyn + f2,
	dx		(1)
. . .
	dyn	= an1y1 + an2y2 + . . . + annyn + fn,
	dx

где функции aij, fj непрерывны по x при x 2 [x1, x2].Тогда система(1)имеет

единственное решение y1(x),0y2(0x), . . . ,0yn(x),принимающее при x =	x0 2 (x1, x2)
любые начальные значения y1 , y2 , . . . , yn .
Это решение существует на всем отрезке [x1, x2].
Коэффициенты разложения функции r(s + s) в ряд по степеням	s выража-

ются только через кривизну и кручение кривой.Это дает основание полагать,что кривизна и кручение в какой-то мере определяют кривую.И действительно,имеет место

Теорема92.2. Пусть k(s) и (s) любые регулярные функции,причем k(s) > 0. Тогда существует,и притом единственная,с точностью до положения в пространстве,кривая,для которой k(s) является кривизной,а (s) кручением в точке,соответствующей дуге s.

Доказательство. Если кривая,существование которой утверждается в теореме, действительно существует,то единичные векторы касательной,главной нормали и бинормали этой кривой t(s), n(s), b(s) удовлетворяют системе дифференциальных

уравнений		8 00	=	k	,
			=	k ,
		< 0	= −	−
в силу формул Френе.		:
Естественно поэтому при разыскании интересующей нас кривой обратиться к
решениям этой системы.
Пусть (s), (s), (s) решение этой системы,удовлетворяющее начальным
условиям:при s = s0 , = 0 , = 0 , = 0 ,где					0, 0, 0 три единичные взаимно
перпендикулярные вектора,смешанное произведение которых						( 0, 0, 0) = 1.
Покажем,что	векторы	(s), (s), (s)			единичные и	взаимно перпенди-
кулярные при	любом s	и ( (s), (s), (s)) = 1.Для				этого вычислим

177

( 2)0, ( 2)0, ( 2)0, ( , )0, ( , )0, ( , )0 .Используя уравнения системы,для этих производных получаем следующие выражения:

( 2)0	= 2k( , ),	( , )0	= k 2 − k 2 − ( , ),
( 2)0	= −2k( , ) − 2 ( , ),	( , )0	= 2 − 2 − k( , ),
( 2)0	= 2 ( , ),	( , )0	= k( , ) + ( , ).

Рассматривая эти равенства как систему дифференциальных уравнений относительно ( 2), ( 2), ( 2), ( , ), ( , ), ( , ),замечаем,что она удовлетворяется значениями2 = 1, 2 = 1, 2 = 1, ( , ) = ( , ) = ( , ) = 0.С другой стороны,эта система удовлетворяется значениями 2 = 2(s), 2 = 2(s), . . . , ( , ) = ( (s), (s)).Оба эти решения совпадают при s = s0 ,а следовательно,по теореме о единственности решения,совпадают тождественно.Тем самым,для всех s

2(s) = 1, 2(s) = 1, . . . , ( , ) = 0.

Покажем,что ( (s), (s), (s)) = 1.Так как , , единичные взаимно перпендикулярные векторы,то ( , , ) = ±1.Смешанное произведение ( , , ) непрерывно зависит от s,при s = s0 оно равно1,поэтому оно равно1для всех s.

Рассмотрим теперь кривую γ ,определяемую векторным уравнением

Z s

r =	(s)ds.
	s0

Параметризация кривой γ естественная.В самом деле,длина дуги отрезка s0s кри-

вой γ равна	Z s	Z s

|r0(s)|ds = | (s)|ds = s − s0.

s0

s0

Кривизна кривой γ равна |r00(s)| = | 0(s)| = k(s).Кручение кривой

γ равно

−

(r0

, r00, r000)

=

−

( , k , k0 + k 0)

=

−

( , k , k0 + k(−k − ))

= (s).

k2

k2

k2

Таким образом,кривая

γ имеет в точке,соответствующей дуге

s,кривизну k(s)

и кручение (s).

Существование кривой доказано.Докажем единственность.

Пусть γ1 и γ2 две кривые,которые в точках,соответствующих дуге

s,имеют

одинаковые кривизны k(s)

и кручения (s).Совместим кривые

γ1 и γ2

точками,

соответствующими дуге s0 и естественными трехгранниками в этих точках.Пусть t1, n1, b1 и t2, n2, b2 единичные векторы касательных,главных нормалей и бинормалей кривых γ1 и γ2 соответственно.

Тройки вектор-функций t1(s), n1(s), b1(s) и t2(s), n2(s), b2(s) являются решениями системы для , , .Начальные значения этих решений совпадают.Отсю-

да следует,что решения совпадают тождественно.В частности t1(s) t2(s) или r01(s) r02(s).Интегрируя это равенство в пределах s0, s,получим:

r1(s) r2(s).

Таким образом,кривая γ2 отличается от γ1 только положением в пространстве. Определение. Система равенств

k = k(s), = (s)

называется натуральными уравнениями кривой.

178

По доказанной теореме,кривая натуральными уравнениями определяется однозначно с точностью до движения.

§93.Эволюта плоской кривой

Определение. Эволютой9 плоской кривой называется огибающая ее нормалей.

Пусть регулярная кривая γ без особых точек задана естественной параметризацией r = r(s), s 2 (a, b).Как известно,уравнение нормали в произвольной точке

кривой имеет вид

(R − r(s), r0(s)) = 0.

Поэтому нормали данной кривой образуют однопараметрическое семейство прямых,где s параметр.Продифференцируем это соотношение по параметру s.Тогда с учетом равенства |r0(s)| = 1 получаем систему уравнений для определения огибающей указанного семейства

(R − r, r0) = 0, (R − r, r00) = 1,

но r0(s) = t(s), r00(s) = k(s)n(s).Поэтому R−r?t.С другой стороны, t ортогонален вектору n,следовательно, n коллинеарен вектору R − r.Тогда для некоторого λ справедливо равенство

R − r(s) = λn(s).

Найдем соответствующее значение λ.Для этого заметим,что

(R − r(s), k(s)n(s)) = 1,

и тогда имеем (λk(s)n, n) = 1,откуда получаем λ = 1/k(s) = p(s).

Определение. Величина p(s),обратная кривизне кривой,называется радиусом кри-

визны.

Таким образом,радиус-вектор R произвольной точки эволюты плоской кривой вычисляется по формуле

R= r(s) + p(s)n(s),

асама эта точка называется центром кривизны. Пусть γ плоская кривая, P точка на ней.

Определение. Окружность ! ,проходящая через точку P ,называется соприкасающейся окружностью кривой γ в точке P ,если кривая в этой точке с окружностью имеет соприкосновение второго порядка.

Теорема93.1.	Радиус соприкасающейся окружности кривой γ ,заданной уравне-
нием r = r(t)	в точке t0 равен 1/k(t0),где k(t0) кривизна кривой γ в точке
t0 .

Доказательство. Пусть ! соприкасающаяся окружность в точке M(x0, y0) кривой γ .Ее уравнение имеет вид

(x − a)2 + (y − b)2 = R2,

9Понятия эволюты и эвольвенты ввел голландский физик,механик,математик,астроном и изобретатель Христиан Гюйгенс(1629–1695).

179

где O(a, b) центр окружности,а R ее радиус.Пусть N(x, y) точка кривой γ , достаточно близкая к точке M ,соответствующая значению параметра t.Пусть L точка пересечения соприкасающейся окружности и отрезка ON (рис. 2).

Расстояние от точки N кривой γ до окружности ! равно LN = ON − OL.Относительно t − t0 оно является бесконечно малым того же порядка,что и ON2 − OL2 ,поскольку

ON2 − OL2 = ON + OL ! 2R при t ! t0.

ON − OL

При этом расстояние MN при N ! M имеет порядок t − t0 :

|MN| = |r(t)−r(t0)| = |r0(t0)(t−t0)+"(t0, t−t0)(t−t0)|.

p

Поскольку |OL| = R, |ON| = (x(t) − a)2 + (y(t) − b)2 ,рассмотрим функцию

'(t) = |ON|2 − |OL|2 = (x(t) − a)2 + (y(t) − b)2 − R2.

Разложим '(t) в ряд Тейлора в окрестности точки t0 :

'(t) = '(t0) + '0(t0)(t − t0) + '00(t0)(t − t0)2 + '000(t0)(t − t0)3 + . . .

2! 3!

Для того чтобы окружность ! была соприкасающейся окружностью кривой γ в точке M ,необходимо и достаточно,чтобы функция '(t) была бесконечно малой не ниже третьего порядка при t ! t0 .Для выполнения последнего условия необходимо и достаточно,чтобы выполнялись равенства

'(t0) = 0, '0(t0) = 0, '00(t0) = 0,

откуда получаем

'(t0) = (x0 − a)2 + (y0 − b)2 − R2 = 0,

'0(t0) = 2[x00(x0 − a) + y00 (y0 − b)] = 0,

'00(t0) = 2[x000(x0 − a) + y000(y0 − b) + x002 + y002] = 0.

Рассматривая последние два уравнения как систему линейных уравнений относительно (x0 − a), (y0 − b),находим

0	x02	+ y02		0	x02	+ y02	00	0	00	0
	0	0			0	0
x0 − a = y0			, b − y0	= x0			, (x0y0		− y0 x0		6= 0).
	x000y00	− y000x00			x000y00	− y000x00

Подставим найденные значения в первое уравнение:

	2		2		2			(x02	+ y02)3	1
R		= (x0 − a)		+ (y0 − b)		=		0	0	=		.
							(x000y00		− y000x00 )2		k2(t0)

Теорема доказана.

Следствие93.1. Уравнение эволюты кривой γ в случае произвольной параметризации x = x(t), y = y(t) имеет вид

X = x − y0 x02 + y02 , Y = y + x0 x02 + y02 .

x0y00 − x00y0 x0y00 − x00y0

180