geometry24

ЛЕКЦИЯ31.УГЛЫ И ПЛОЩАДИ.КОНФОРМНЫЕ ОТОБРАЖЕНИЯ

§103.Угол между кривыми на поверхности

Определение. Направлением (du : dv) на поверхности Φ называется направление вектора dr = rudu + rvdv.

Это направление будем также называть просто (d).

Определение. Углом между направлениями (du : dv) и (δu : δv) называется угол между векторами

dr = rudu + rvdv и δr = ruδu + rvδv.

Найдем угол между направлениями (d) и (δ).

(dr, δr) = |dr||δr| cos ,

dr2 = Edu2 + 2F dudv + Gdv2 = I(d), δr2 = Eδu2 + 2Fδuδv + Gδv2 = I(δ),

(dr, δr) = Eduδu + F (duδv + δudv) + Gdvδv = I(d,δ ).

Отсюда

cos = pI(d,δ ) . I(d)I(δ)

Определение. Говорят,что кривая γ на поверхности,заданной уравнением r = r(u, v) в точке (u, v) имеет направление (du : dv),если вектор dr = rudu + rvdv является касательным вектором кривой в этой точке.

Кривая на поверхности,заданная уравнениями u = u(t), v = v(t) в точке t имеет направление (u0(t) : v0(t)).

Определение. Если две кривые γ и γ¯ на поверхности Φ имеют общую точку (u, v), то углом между ними в точке (u, v) называется угол между их направлениями в этой точке.

Тем самым,угол между кривыми на поверхности это угол между касательными к этим кривым,и он не зависит ни от параметризации поверхности,ни от параметризации кривых.

Пример103.1. Координатные линии на поверхности( u = const и v = const)имеют направления (0 : dv), (δu : 0).Поэтому угол между координатными линиями находится по формуле

		F dvδu				F
cos =	p		p		=	p		.
		Gdv2		Eδu2			EG

Отсюда следует,что координатная сеть на поверхности ортогональна(координатные линии пересекаются под прямым углом)тогда и только тогда,когда F = 0.

§104.Площадь поверхности

Найдем площадь области G на гладкой поверхности Φ,причем область G определяется параметризацией r = r(u, v), (u, v) 2 D,где D некоторая плоская область.

201

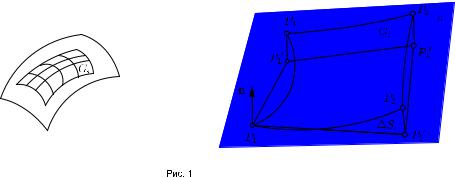
Разобьем область G на области G1, G2, . . . , Gn .В какой-либо точке каждой из областей Gi построим касательную плоскость и на нее спроектируем соответствующую область.

Пусть Si площадь плоской области,получившейся после проектирования

Gi .Составим сумму

Xn

Sn =	Si.
	i=1

Определение. Площадью области G на поверхности называется предел S суммы Sn при неограниченном убывании областей Gi по своим размерам

S = lim Sn.

Выберем границы областей Gi

так,чтобы они совпадали с координатными ли-

ниями.Рассмотрим одну из этих областей

Gi ,предположив,что ограничивающие ее

кривые пересекаются в точках P1(u(i), v(i)), P2(u(i) +

u(i), v(i)), P3(u(i) +

u(i), v(i) +

v(i)), P4(u(i), v(i) + v(i)).

Спроектировав эту область на касательную плоскость в точке P1(u(i), v(i)),

получаем криволинейный четырехугольник P1P20P30P40 .

В силу формулы Тейлора

(i)

(i)

(i)

(i) (i)

(i)

(i)

P1P2 = r(u(i) +(i)

u

, v(i) ) − r(u(i) , v(i) ) = ru

u(i)

+ "1 u(i) ,

P1P4 = r(u , v + v ) − r(u , v ) = rv v

+ "2 v ,

причем lim "1

= 0, lim "2 = 0.

u!0

v!0

Пренебрегая малыми более высокого порядка малости,мы можем принять про-

екции векторов P1P2 и P1P4 равными векторам ru

u(i)

и rv v(i) .

И снова,отбросив малые более высокого порядка,заменим площадь

Si

плоской

проекции P1P20P30P40 площадью параллелограмма,построенного на векторах

ru u(i)

и rv v(i) как на сторонах.

Получаем

Si = |[ru(u(i), v(i)), rv(u(i), v(i))]| u(i)

v(i) ,

(i) !

n

Xi

u(i)

(i)

S = lim Sn =

lim

0, =1 |

[r

, r ]

|

v

.

u(i)

u

v

v

! 0,

n ! 1

Таким образом,площадь области

G заданной поверхности выражается двойным ин-

тегралом

S = Z ZD |[ru, rv]|dudv.

202

Поскольку

|[ru, rv]|2 = r2ur2v − (ru, rv)2 = EG − F 2,

то Z Z p

S = EG − F 2dudv.

D

Можно показать,что интеграл не зависит от выбора параметризации(из свойств интеграла).

§105.Конформные отображения

Определение. Пусть Φ1 и Φ2 регулярные поверхности.Топологическое отображение поверхности Φ1 на поверхность Φ2 называется конформным,если оно сохраняет углы между кривыми(соответствующие кривые пересекаются под одинаковыми углами).

Теорема105.1. Если регулярные поверхности Φ1 и Φ2 параметризованы так,что коэффициенты их первых квадратичных форм пропорциональны,то отображение одной поверхности на другую,при котором сопоставляются точки с одинаковыми координатами,конформно.

Обратно,если поверхности Φ1 и Φ2 параметризовать так,что соответствие точек с одинаковыми координатами конформно,то первые квадратичные формы поверхностей пропорциональны.

Доказательство. Пусть

I1 = Edu2 + 2F dudv + Gdv2,

I2 = λ(Edu2 + 2F dudv + Gdv2)

первые квадратичные формы поверхностей Φ1 и Φ2 .Если отображение Φ1 на Φ2 состоит в сопоставлении точек с одинаковыми координатами,то соответствующие кривые имеют одинаковые внутренние уравнения u = u(t), v = v(t),следовательно, для угла между соответствующими кривыми получается одно и то же выражение, т.е.отображение конформно.Первая часть теоремы доказана.

Пусть (u, v) произвольная параметризация поверхности Φ1 .Параметризуем поверхность Φ2 ,сопоставляя произвольной ее точке в качестве координат координаты соответствующей точки Φ1 при конформном отображении.Пусть

I1 = E1du2 + 2F1dudv + G1dv2,

I2 = E2du2 + 2F2dudv + G2dv2

первые квадратичные формы поверхностей,соответствующие этим параметризациям.Покажем,что коэффициенты этих квадратичных форм пропорциональны.

В силу конформности отображения ортогональность направлений (d) и (δ) относительно формы I1 влечет их ортогональность относительно формы I2 .Поэтому из

I1 = E1duδu + F1(duδv + δudv) + G1dvδv = 0

следует

E2duδu + F2(duδv + δudv) + G2dvδv = 0.

Отсюда,исключая δu,δv ,получаем

E1du + F1dv	=	F1du + G1dv	.
E2du + F2dv	F2du + G2dv

203

Ввиду произвола du и dv при dv = 0 получаем

E1 = F1 ,

E2 F2

а при du = 0

F1 = G1 .

F2 G2

Теорема доказана полностью.

Конформное отображение обладает еще одним замечательным свойством. Утверждение. Достаточно малые соответствующие фигуры на поверхностях

при конформном отображении в первом приближении подобны. Доказательство. Пусть F1 малая фигура на поверхности Φ1 .Расстояние между ее точками (u, v) и (u + u, v + δv) в первом приближении равно

p

Eδu2 + 2Fδuδv + Gδv2.

Расстояние между соответствующими точками фигуры F2 на поверхности Φ2 в первом приближении равно

p

λ(Eδu2 + 2Fδuδv + Gδv2).

Таким образом,коэффициент искажения равен λ и,следовательно,почти постоянен, если фигура F1 достаточно мала.

Теорема105.2. Пусть Φ1 и Φ2 регулярные поверхности, P1, P2 произвольные точки на этих поверхностях.Тогда существует конформное отображение некоторой окрестности точки P1 поверхности Φ1 на некоторую окрестность точки P2 поверхности Φ2 .

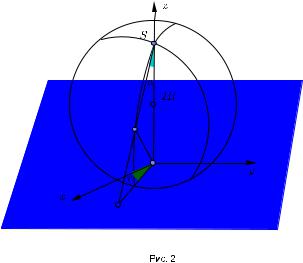
Пример105.1. Конформное отображение сферы на плоскость.

Пусть ! сфера радиусом R с центром в точке (0, 0, R).Рассмотрим отображение сферы ! на плоскость xy,которое заключается в проектировании ее из полюса

S(0, 0, 2R).Это отображение называется стереографической проекцией.

Введем в качестве криволинейных координат углы u и v,показанные на рис2. Тогда уравнения плоскости

x = 2R tg u cos v, y = 2R tg u sin v, z = 0

а сферы

x = 2R sin u cos u cos v, y = 2R sin u cos u sin v, z = 2R sin2 u.

Для плоскости
	2R			2R
ru =		cos v,				sin v, 0 , rv = (−2Rtg u sin v, 2Rtg u cos v, 0).
	cos2 u			cos2 u
				4R2
E1 = (ru, ru) =					, F1 = (ru, rv) = 0, G1 = (rv, rv) = 4R2tg2 u.
			cos4 u

Для сферы перепишем уравнение следующим образом:

r = (R sin 2u cos v, R sin 2u sin v, z = 2R sin2 u).

204

Имеем

ru = (2R cos 2u cos v, 2R cos 2u sin v, 4R sin u cos u) =

= (2R cos 2u cos v, 2R cos 2u sin v, 2R sin 2u),

rv = (−R sin 2u sin v, R sin 2u cos v, 0),

откуда

E2 = 4R2, F2 = 0, G2 = R2 sin2 2u.

Тем самым,получаем,что линейный элемент плоскости равен

	4R2
ds2 =		(du2	+ sin2 u cos2 udv2),
	cos4 u

а сферы

ds2 = 4R2(du2 + sin2 u cos2 udv2).

Отсюда заключаем,что отображение конформно.

Первая квадратичная форма поверхности определяет внутреннюю геометрию поверхности,т.е.совокупность фактов,которые могут быть получены при помощи измерений,полученных на самой поверхности,без обращения к объемлющему пространству.Внутренняя геометрия поверхности является широким обобщением планиметрии.Роль прямых во внутренней геометрии произвольной поверхности играют геодезические линии линии на поверхности,достаточно малые дуги которых являются на этой поверхности кратчайшими путями между их концами.Две поверхности имеют одинаковую внутреннюю геометрию,если можно их отобразить взаимно однозначно одну на другую так,что геодезические линии перейдут в геодезические и длина их останется неизменной.Такие поверхности называются изометричными. Непрерывная деформация поверхности,при которой ее внутренняя геометрия все время остается неизменной,называется изгибанием поверхности.Если поверхность физически реализована из гибкого,но нерастяжимого материала,то,деформируя ее так,чтобы не возникало складок или разрывов,получают изгибание этой поверхности.Исследование изгибаний имеет важное значенив теории упругих оболочек.

§106.Вторая квадратичная форма поверхности

Пусть Φ регулярная поверхность, r = r(u, v) какая-нибудь ее регулярная праметризация, n(u, v) единичный вектор нормали к поверхности в точке P (u, v).

205

Второй квадратичной формой поверхности называется квадратичная форма

II = −(dr, dn) = (−(ru, nu))du2 + (−(ru, nv) − (rv, nu))dudv + (−(rv, nv))dv2.

Для коэффициентов этой формы вводятся следующие обозначения

−(ru, nu) = L, −(ru, nv) − (rv, nu) = 2M, −(rv, nv) = N.

Так как (dr, n) = 0 и,следовательно,

d(dr, n) = (d2r, n) + (dr, dn) = 0,

то

II = (d2r, n) = (ruu, n)du2 + 2(ruv, n)dudv + (rvv, n)dv2.

Отсюда

L = (ruu, n), M = (ruv, n), N = (rvv, n).

Так как n =

[ru, rv]

, а |[ru, rv]| =

p

, то

EG − F

2

|[ru, rv]|

"

xuu

yuu

zuu

"

|

|

xu

yu

zu

"

−

"

(ruu, ru, rv)

"

xv

yv

zv

"

"

"

L =

=

"

"

,

"

"

[ru, rv]

pEG F

2

"

xuv

yuv

zuv

"

|

|

xu

yu

zu

"

−

"

(ruv, ru, rv)

"

xv

yv

zv

"

"

"

M =

=

"

"

,

"

"

[ru, rv]

pEG F

2

"

xvv

yvv

zvv

"

|

|

xu

yu

zu

"

−

"

(rvv, ru, rv)

"

xv

yv

zv

"

"

"

N =

=

"

"

.

"

"

[ru, rv]

pEG F

2

В частности,если поверхность задана уравнением							z = z(x, y), то
		zxx			zxy				zyy
L =			, M =			, N =				.
	p			p				p
		1 + zx2 + zy2			1 + zx2 + zy2				1 + zx2 + zy2

206

ЛЕКЦИЯ32.КРИВИЗНЫ
§107.Кривизна кривой,лежащей на поверхности
Пусть Φ регулярная поверхность, r = r(u, v) какая-нибудь ее регулярная
параметризация, γ кривая на поверхности,проходящая
через точку P (u, v) и имеющая в этой точке направление
(du : dv).Пусть r = r(s) естественная параметризация
кривой γ .
Рассмотрим скалярное произведение (r00, n).Вектор
r00 направлен по главной нормали кривой,а по длине ра-
вен кривизне кривой.Отсюда	(r00, n) = k cos ,где	k
кривизна кривой,а угол,образуемый главной норма-
лью кривой и нормалью к поверхности(рис. 1).

Но

(r00, n) = (ruuu02 + 2ruvu0v0 + rvvv02 + ruu00 + rvv00, n) = = (ruu, n)u02 + 2(ruv, n)u0v0 + (rvv, n)v02.

Поэтому

	Ldu2 + 2Mdudv + Ndv2		II
k cos =		=		.
	Edu2 + 2F dudv + Ndv2		I

Правая часть этого равенства зависит только от направления кривой в точке P (u, v). Таким образом, k cos = k0 = const для всех кривых γ ,проходящих через эту точку и имеющих в ней одно и то же направление(одну и ту же касательную).

Это равенство теорема Мёнье11.

Определение. Величина k0 называется нормальной кривизной поверхности в данном направлении (du : dv).

С точностью до знака нормальная кривизна равна кривизне кривой,которая получается в сечении поверхности плоскостью,перпендикулярной касательной плоскости

и содержащей направление (du : dv).

Отложим из произвольной точки P (u, v) поверхности в каждом направлении (du : dv) отрезок,равный |1/k|1/2 , где k нормальная кривизна поверхности в данном на-

правлении(рис. 2).

Определение. Геометрическое место концов этих отрезков называется индикатри-

сой кривизны поверхности в точке P ,или индикатрисой Дюпена12.

В касательной плоскости поверхности введем координаты с началом в точке касания,прямые,содержащие векторы ru и rv ,выберем за оси координат,а сами векторы ru и rv за базисные векторы.Пусть (x, y) координаты точки индикатрисы кривизны,соответствующей направлению (du : dv).Имеем

xru + yrv = |1/k|1/2 rudu + rvdv . |rudu + rvdv|

11Жан Батист Мари Шарль Мёнье де ла Плас(1754–1799) французский математик,дивизионный генерал,считается изобретателем дирижабля.

12Дюпен Пьер Жан Франсуа(1784–1873) французский математик.

207

Возводя это равенство в квадрат и замечая,что x : y = du : dv,получаем

	Ex2	+ 2F xy + Gy2 =		Edu2	+ 2F dudv + Gdv2			=
				|Ldu2	+ 2Mdudv + Ndv2		|
			Ex2 + 2F xy + Gy2
		=				.
			|Lx2 + 2Mxy + Ny2|

Отсюда |Lx2 + 2Mxy + Ny2| = 1.

Это и есть уравнение индикатрисы кривизны.

Таким образом,индикатриса кривизны представляет собой эллипс в эллиптической точке поверхности( LN − M2 > 0),пару сопряженных гипербол в гиперболической точке( LN − M2 < 0),пару параллельных прямых в параболической точке( LN − M2 = 0).

Индикатрису кривизны можно ввести другим способом.Пусть P произвольная точка поверхности и касательная плоскость в этой точке.Обозначим Mh геометрическое место точек поверхности,расстояние которыхpдо равно h.Сделаем преобразование подобия с центром P с коэффициентом 1/ h.Полученное множество точек обозначим 1/phMh .

Уравнение поверхности,если касательную плоскость в P принять за плоскость

xy,а нормаль за ось z,будет

z =

1

(rx2

+ 2sxy + ty2) + (x2 + y2)"(x, y),

2

где " ! 0 при x, y ! 0.В самом деле,оба вектора

rx и ry лежат в касательной

плоскости,значит, zx = zy = 0 в точке P .Отсюда точки Mh

удовлетворяют уравне-

нию

1

h =

|(rx2 + 2sxy + ty2) + (x2 + y2)"(x, y)|.

2

Так как координаты точки из

p

отличаются от координат соответствующей

1/ hMh

точки из Mh множителем ph,то они удовлетворяют уравнению

1

2

2

2

2

p

p

|(rx

h)|.

1 =

+ 2sxy + ty

) + (x

+ y

)"(x h, y

2

Отсюда видно,что 1/

p

сходится к индикатрисе кривизны при h ! 0.

hMh

§108.Асимптотические направления.Асимптотические линии.Сопряженные направления

Определение. Направление (du : dv) на регулярной поверхности в точке P (u, v) называется асимптотическим,если нормальная кривизна поверхности в этом направлении равна нулю.

Таким образом,направление (du : dv) будет асимптотическим тогда и только тогда,когда выполняется условие

Ldu2 + 2Mdudv + Ndv2 = 0.

Отсюда следует,что в эллиптической точке поверхности не существует асимптотических направлений,в гиперболической точке существует два асимптотических направления,в параболической точке одно асимптотическое направление,в точке уплощения любое направление является асимптотическим.

208

Определение. Кривая на поверхности называется асимптотической,если ее направление в каждой точке является асимптотическим.

Очевидно,что любая прямая,лежащая на поверхности,будет асимптотической линией.

Утверждение. Касательная плоскость поверхности в каждой точке асимптотической линии является соприкасающейся плоскостью.

Доказательство. Если в точке P асимптотической линии γ кривизна равна нулю, то касательная плоскость поверхности в точке P является соприкасающейся,так как она проходит через касательную к кривой.Если же кривизна γ в точке P отлична от нуля,то касательная плоскость содержит векторы d2r (так как кривая γ асимптотическая и удовлетворяет условию (d2r, n) = 0 и dr (так как плоскость касательная).Следовательно,касательная плоскость является соприкасающейся плоскостью асимптотической кривой.

Очевидно,что координатные линии u = const и v = const будут асимптотическими тогда и только тогда,когда коэффициенты L и N второй квадратичной формы нулевые(подставляем уравнения координатных линий в уравнение асимптотических).

Определение. Говорят,что координатная сеть в этом случае будет асимптотической.

Определение. Пусть P произвольная точка поверхности Φ, (du : dv) и (δu : δv)два направления в точке P на поверхности.Направления (d) и (δ) называются сопряженными,если содержащие их прямые gd иgδ являются сопряженными диаметрами индикатрисы Дюпена в точке P .

Таким образом,для того,чтобы направления (d) и (δ) были сопряженными, необходимо и достаточно выполнения условия

Lduδu + M(duδv + δudv) + Ndvδv = 0.

Иначе

(dr, δn) = 0 или (δr, dn) = 0.

Асимптотические направления являются самосопряженными.

§109.Главные кривизны

Определение. Направление (du : dv) на поверхности называется главным,если нормальная кривизна поверхности в этом направлении достигает экстремального значения.

Таким образом,главные направления это направления осей индикатрисы кривизны.

Таким образом,в каждой точке поверхности в общем случае имеется два главных направления.Совпадая с направлениями осей индикатрисы кривизны,главные направления ортогональны и сопряжены,следовательно,удовлетворяют условиям

I(d,δ ) = Eduδu + F (duδv + δudv) + Gdvδv = 0

(ортогональность)

II(d,δ ) = Lduδu + M(duδv + δudv) + Ndvδv = 0

(сопряженность).

209

Исключая из этих уравнений δu и δv,получим необходимое и достаточное усло-

вие того,чтобы направление		(du : dv)			было главным направлением:
"	Edu + F dv				F du + Gdv				"
"									"
"	Ldu + Mdv				Mdu + Ndv				"	= 0.
Иначе,в более симметричной"		форме:							"
		"	E	− F		G	"	= 0.
		"	L		M	N	"
		"	dv2	dudv		du2	"
		"					"
		"					"
		"					"

Главные направления не определены в двух случаях:в случае точки уплощения любое направление в ней является главным(нормальная кривизна в любом направлении равна нулю)и в специальном случае эллиптической точки,когда индикатриса кривизны круг,такая точка называется шаровой.В шаровой точке,как и в точке уплощения,любое направление является главным.Это условие отражено в уравнении для главных направлений.Определитель равен нулю тождественно только при L = M = N = 0 (точка уплощения)и в случае пропорциональности коэффициентов первой квадратичной формы коэффициентам второй квадратичной формы(шаровая точка).

Определение. Нормальные кривизны поверхности,соответствующие главным направлениям,называются главными кривизнами.

Теорема109.1. (Родриг13)Если направление (d) является главным направлением, то

dn = −kdr,

где k нормальная кривизна поверхности в этом направлениии.Обратно,если в направлении (d)

dn = λdr,

то (d) является главным направлением.

Доказательство. Пусть (δ) другое главное направление,перпендикулярное первому.Вектор dn,будучи перпендикулярным n,допускает представление

dn = λdr + µδr.

Умножая это равенство на δr и замечая,что (dn, δr) = 0 в силу сопряженности направлений (d) и (δ), и (dr, δr) = 0 в силу ортогональности этих направлений, получим

µδr2 = 0,

откуда µ = 0.Итак, dn = λdr.Умножая это равенство на dr,получим

(dr, dn) = λdr2.

Отсюда следует,что λ = −k.

Докажем обратное утверждение.Пусть направление (d) таково,что dn = λdr. Пусть (δ) направление,перпендикулярное (d).Тогда,умножая равенство dn = λdr на δr,получим (dn, δr) = 0.Значит,направления (d) и (δ) сопряженные.Так как они,кроме того,ортогональны,то они главные.

13Родриг Бенжамен Оленд(1794–1851) французский банкир,математик и социальный реформатор.

210