
- •Глава II. Дифференциальное исчисление функций одной переменной
- •2.1. Производная функции
- •2.1.1. Определение производной функции
- •2.1.2. Дифференцируемость функции, ее взаимосвязь с производной и непрерывностью функции
- •2.1.3. Непосредственное нахождение производной
- •2.1.4. Геометрический смысл производной
- •2.1.5. Механический смысл производной
- •2.1.6. Правила дифференцирования функций
- •2.1.7. Вывод производных основных элементарных функций
- •2.1.8. Сводка формул Правила дифференцирования
- •2.1.9. Производные высших порядков
- •2.1.10. Эластичность функции
- •2.1.11. Геометрический смысл эластичности
- •2.1.12. Экономический смысл эластичности
- •2.1.13. Свойства эластичности функции
- •2.2. Дифференциал функции одной переменной
- •2.2.1. Определение дифференциала функции
- •2.2.2. Геометрический смысл дифференциала
- •2.2.3. Свойства дифференциала
- •2.2.4. Применение дифференциала для приближенных вычислений
- •2.2.5. Дифференциалы высших порядков
- •2.3. Теоремы о дифференцируемых функциях
- •2.3.1. Теорема Ролля
- •2.3.2. Геометрический смысл теоремы Ролля
- •2.3.3. Примеры использования теоремы Ролля
- •2.3.4. Теорема Лагранжа о конечном приращении функции
- •2.3.5. Геометрический смысл теоремы Лагранжа
- •2.3.6. Теорема Коши
- •2.3.7. Раскрытие неопределенностей при нахождении пределов. Правило Лопиталя
- •2.3.8. Применение правила Лопиталя для раскрытия неопределенностей типа степени
- •2.4. Формулы Тейлора и Маклорена
- •2.4.1. Формула Тейлора. Остаточный член в форме Лагранжа
- •2.4.2. Формула Маклорена
- •2.4.3. Разложение основных элементарных функций по формуле Маклорена
- •2.4.4. Применение формулы Маклорена для вычисления пределов и значений функций
- •2.5. Исследование функций
- •2.5.1. Необходимый и достаточный признаки монотонности функций
- •2.5.2. Определение экстремума функции
- •2.5.3. Необходимый признак экстремума функции
- •2.5.4. Первый достаточный признак экстремума функции (с использованием первой производной)
- •2.5.5. Второй достаточный признак экстремума функции (с использованием производной второго порядка)
- •2.5.6. Определение выпуклости, вогнутости графика функции, точки перегиба
- •2.5.7. Достаточный признак выпуклости, вогнутости графика функции
- •2.5.8. Необходимый признак существования точки перегиба
- •2.5.9. Достаточный признак существования точки перегиба
- •2.5.10. Асимптоты графика функции
- •2.5.11. Построение графика функции
2.5.11. Построение графика функции
Будем использовать следующую общую схему исследования функции и построения графика.
1. Найти область определения функции.
2. Определить общий
вид функции. Если
![]() ,
то функция четная; если
,
то функция четная; если
![]()
функция нечетная; если
функция нечетная; если
![]()
периодическая (а
– период); иначе будем функцию называть
общего вида (ФОВ).
периодическая (а
– период); иначе будем функцию называть
общего вида (ФОВ).
3. Найти точки пересечения с осями координат.
4. Найти вертикальные и наклонные асимптоты.
5. Найти интервалы монотонности и экстремумы функции (исследование с помощью первой производной).
6. Найти интервалы выпуклости, вогнутости графика функции и точки перегиба (исследование с помощью производной второго порядка).
7. Построить график.
Пример
2.24.
Исследовать и построить график функции
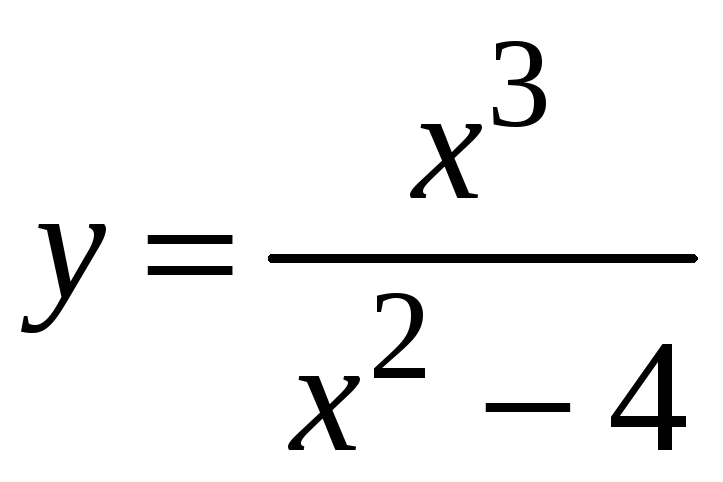 .
.
1. Область определения
функции
![]() .
.
2. Находим
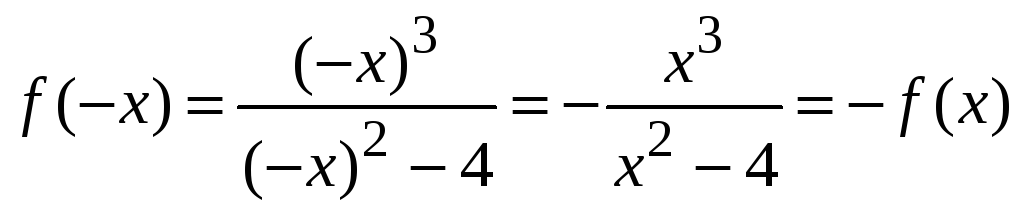 .
Функция нечетная.
.
Функция нечетная.
3. Асимптоты графика функции найдены в предыдущем примере;
х =
2
и х =
+2 – вертикальные асимптоты;
![]()
наклонная асимптота.
наклонная асимптота.
4. Найдем точки пересечения с осями координат. Единственная точка O(0, 0) начало координат.
5. Найдем производную функции
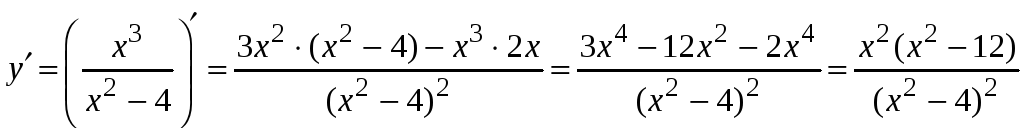 .
.
Находим критические
точки
![]() .
.
Определяем интервалы монотонности и экстремумы функции (рис. 43).

Рис. 43
На числовую ось
нанесем критические точки
![]() и точки разрыва функции
и точки разрыва функции
![]() ,
которые разобьют эту прямую на интервалы
монотонности. Чтобы не ошибиться при
определении знака производной в
интервалах, точки, в которых производная
не изменяет знак, отметим значком
«кавычка». Знаки производной в интервалах
отметим знаком «+» или «».
Характер монотонности функции на
интервалах отметим стрелками. Если в
критической точке функция непрерывна
и характер монотонности изменяется, то
точка является точкой экстремума. Для
рассматриваемой функции точка
,
которые разобьют эту прямую на интервалы
монотонности. Чтобы не ошибиться при
определении знака производной в
интервалах, точки, в которых производная
не изменяет знак, отметим значком
«кавычка». Знаки производной в интервалах
отметим знаком «+» или «».
Характер монотонности функции на
интервалах отметим стрелками. Если в
критической точке функция непрерывна
и характер монотонности изменяется, то
точка является точкой экстремума. Для
рассматриваемой функции точка
![]() является точкой максимума, а точка
является точкой максимума, а точка
![]() -
точкой минимума. Значение функции в
точках максимума и минимума равняется
-
точкой минимума. Значение функции в
точках максимума и минимума равняется
![]() ,
,
![]() .
.
6. Найдем производную функции второго порядка
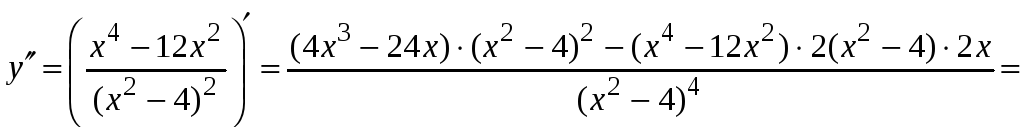
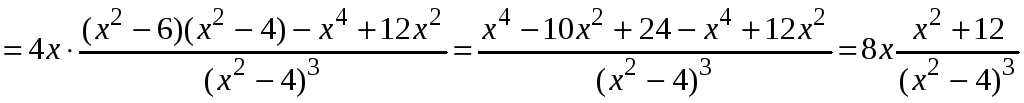 .
.
Находим критические точки для второй производной.
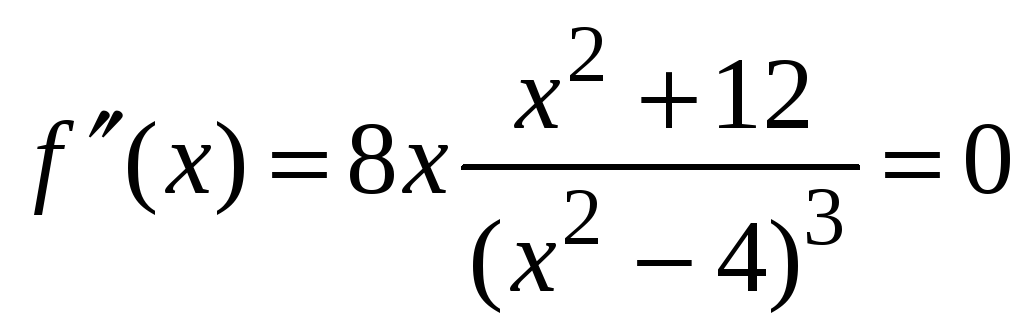 только при х
= 0.
только при х
= 0.
Наносим на числовую прямую критическую точку х = 0 и точки разрыва производной второго порядка (рис. 44).
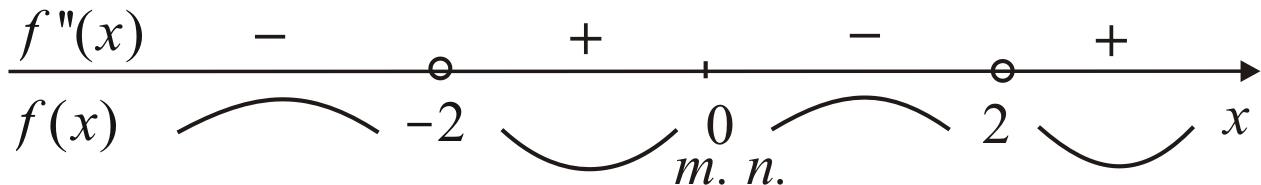
Рис. 44
Определяем знаки
второй производной в получившихся
интервалах. Знаку «+» соответствует
вогнутость, а знаку «»
выпуклость графика функции. В точке х
= 0 график функции имеет точку перегиба,
так как функция непрерывная в этой
точке, а характер кривой изменяется с
вогнутости на выпуклость. Функция в
этой точке равна нулю
![]() .
.
7. Изображаем график функции (рис. 45). Строим систему координат Oxy, асимптоты, точки максимума, минимума и точку перегиба.
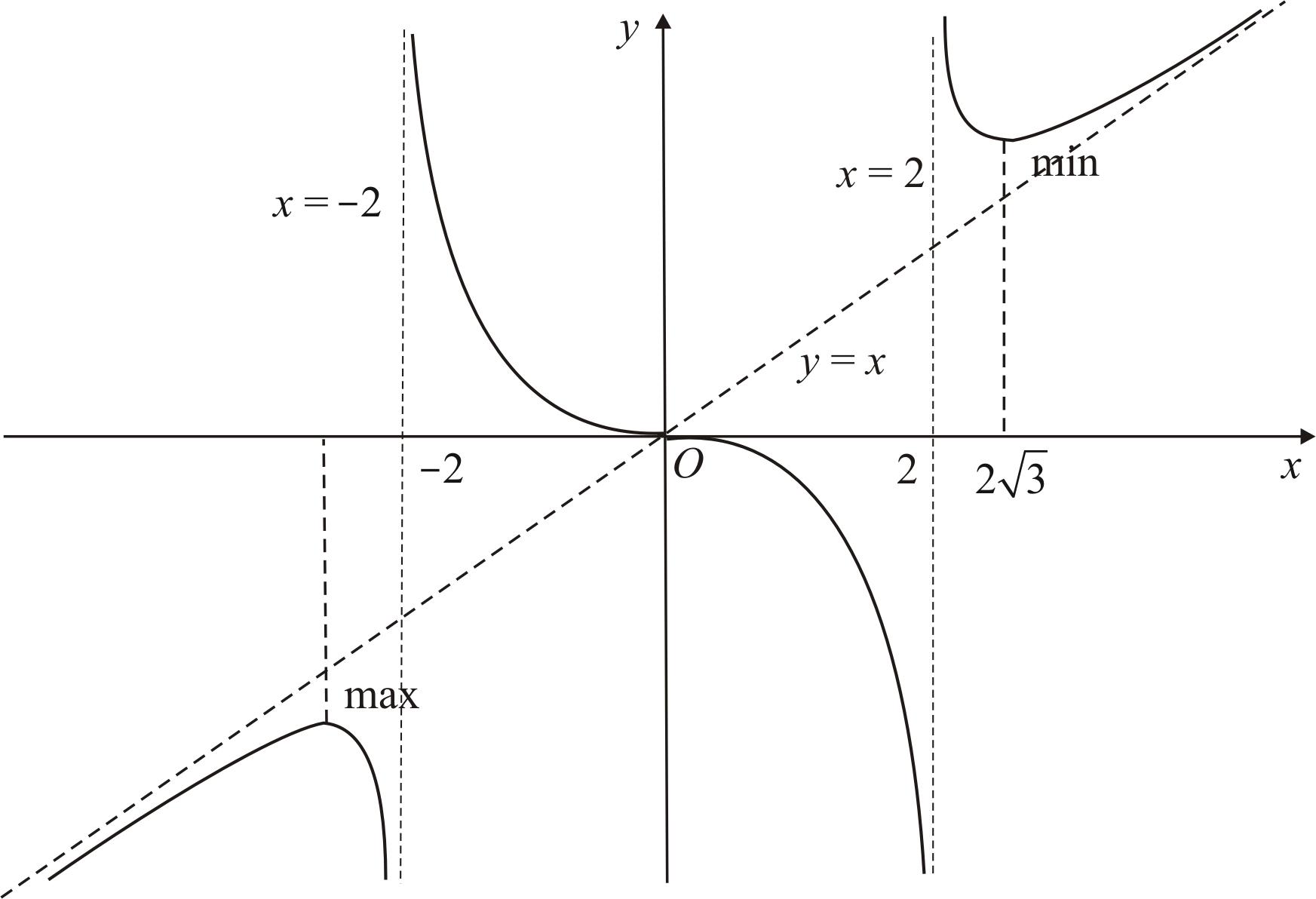
Рис. 45
